Serie de Fourier para niños
Una serie de Fourier es una herramienta matemática muy útil que nos ayuda a entender y trabajar con funciones que se repiten, como las ondas. Imagina que tienes una canción compleja. Una serie de Fourier te permite descomponer esa canción en muchas ondas de sonido más simples, como si separaras los sonidos de cada instrumento.
Esta idea fue desarrollada por un matemático francés llamado Jean-Baptiste Joseph Fourier a principios del siglo XIX. Él estaba estudiando cómo se propaga el calor en los objetos y descubrió que podía usar estas series para describir cómo el calor se movía. Por eso, a veces, a esta área de estudio se le llama análisis armónico, que es como estudiar las "armonías" o componentes de las ondas.
Las series de Fourier son muy importantes en muchas áreas de la ciencia y la ingeniería. Nos ayudan a entender las vibraciones, el sonido, la luz, cómo funcionan las señales en la televisión o el internet, y hasta cómo se guardan las imágenes y los sonidos en tu computadora o teléfono.
Contenido
¿Qué es una serie de Fourier?
Una serie de Fourier es una forma de representar una función que se repite (una función periódica) como una suma de muchas ondas simples. Estas ondas simples son funciones de seno y coseno, que son las formas más básicas de las ondas.
Imagina que tienes una onda con una forma muy extraña. La serie de Fourier te dice que esa onda extraña puede ser el resultado de sumar muchas ondas de seno y coseno de diferentes tamaños y velocidades. Es como si cada onda de seno o coseno fuera un "ingrediente" que, al mezclarse, forma la onda original.
¿Cómo se usan las series de Fourier?
Las series de Fourier tienen muchas aplicaciones prácticas:
- En la música y el sonido: Ayudan a analizar los sonidos, separando las diferentes frecuencias que componen una nota musical o una voz. Esto es útil para crear efectos de sonido o para mejorar la calidad del audio.
- En la electrónica: Permiten entender cómo se comportan las señales eléctricas en los circuitos. Por ejemplo, en los teléfonos móviles o la radio, las señales se transmiten como ondas, y las series de Fourier ayudan a diseñar los sistemas para que esas señales viajen bien.
- En el procesamiento de imágenes: Se usan para comprimir imágenes (hacerlas más pequeñas sin perder mucha calidad) o para mejorar su nitidez.
- En la medicina: Ayudan a analizar señales del cuerpo, como las ondas cerebrales o los latidos del corazón.
- En la ingeniería civil: Para estudiar cómo vibran los edificios o puentes y asegurarse de que sean seguros.
Historia de las series de Fourier
La historia de las series de Fourier comienza con Jean-Baptiste Joseph Fourier. Él nació en Francia en 1768. Su trabajo más famoso fue sobre la teoría del calor. En 1807, publicó un estudio donde mostraba cómo se podía usar una suma de funciones de seno y coseno para describir la distribución del calor en un objeto.
Antes de Fourier, otros matemáticos como Leonhard Euler y Daniel Bernoulli ya habían trabajado con ideas similares, pero Fourier fue quien las desarrolló de manera más completa y las aplicó a problemas físicos.
La idea de Fourier era muy innovadora. Él propuso que cualquier función periódica, incluso una muy complicada, podía ser escrita como una suma de ondas simples. Al principio, sus ideas fueron un poco difíciles de aceptar para otros matemáticos, pero con el tiempo se demostró su gran utilidad y precisión.
Después de Fourier, otros matemáticos como Peter Gustav Lejeune Dirichlet y Bernhard Riemann hicieron que las ideas de Fourier fueran aún más precisas y formales, lo que ayudó a que se usaran en más campos de las matemáticas y la ciencia.
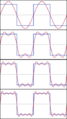
Ejemplos visuales de series de Fourier
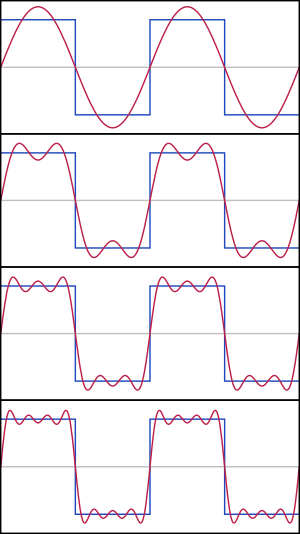
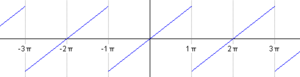
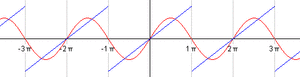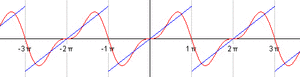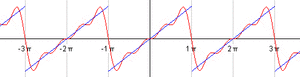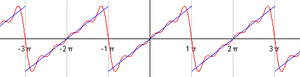
Para entender mejor, mira las imágenes. La primera imagen muestra cómo una función que parece una escalera (una onda cuadrada) puede ser formada sumando varias ondas de seno y coseno. Cada vez que sumamos más ondas, la forma se parece más a la onda original.
La animación muestra cómo, al añadir más y más ondas simples (llamadas "armónicos"), la suma de estas ondas se va acercando cada vez más a la forma de la función original. Es como si cada armónico fuera un pincel que añade un detalle a la pintura final.
Galería de imágenes
-
Las primeras cuatro aproximaciones para una función periódica escalonada
-
Gráfico de una función periódica.
-
Animación de la suma de los 5 primeros armónicos.
Véase también
En inglés: Fourier series Facts for Kids
