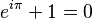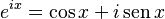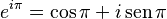Identidad de Euler para niños
En matemáticas, la identidad de Euler es una ecuación muy famosa y especial:
Esta ecuación conecta cinco números muy importantes en matemáticas:
- e es el número de Euler, un número especial que aparece mucho en el estudio del crecimiento y el cambio. Es la base de los logaritmos naturales.
- i es la unidad imaginaria. Es un número que, cuando lo multiplicas por sí mismo (lo elevas al cuadrado), el resultado es -1. Se usa para trabajar con números complejos.
- π (pi) es el número pi. Es la relación constante entre la distancia alrededor de un círculo (su perímetro) y la distancia a través de él (su diámetro).
- 1 es el número uno, que no cambia otros números cuando los multiplicas por él.
- 0 es el número cero, que no cambia otros números cuando los sumas o restas.
Esta identidad es considerada muy hermosa por los matemáticos porque une diferentes áreas de las matemáticas que a primera vista parecen no tener relación.
Contenido
¿Por qué la identidad de Euler es tan especial?
La identidad de Euler es un ejemplo de lo que se llama "belleza matemática". Es especial por varias razones:
¿Qué operaciones matemáticas usa?
En la identidad de Euler, las tres operaciones básicas de la aritmética aparecen una vez cada una:
- La suma (el signo +)
- La multiplicación (implícita entre i y π, y entre e y la potencia)
- La exponenciación (elevar e a la potencia iπ)
¿Qué números fundamentales conecta?
Esta identidad relaciona cinco constantes matemáticas muy importantes:
- El número 0, que es el elemento neutro de la suma.
- El número 1, que es el elemento neutro de la multiplicación.
- El número π (aproximadamente 3.1415...), una constante fundamental de los círculos.
- El número e (aproximadamente 2.718...), también conocido como número de Euler, muy importante en el análisis matemático.
- El número i, la unidad imaginaria de los números complejos.
Además, la ecuación está escrita de una forma en la que todo es igual a cero, lo cual es común en muchas áreas de las matemáticas.
¿Qué dicen los expertos sobre ella?
Muchos matemáticos han hablado de la belleza de esta identidad.
- El profesor de matemáticas Keith Devlin de la Universidad de Stanford dijo que la ecuación de Euler "llega hasta lo más profundo de la existencia", como una obra de arte.
- Paul Nahin, profesor de la Universidad de New Hampshire, la describió como "de una belleza exquisita".
- La escritora de matemáticas Constance Reid la llamó "la fórmula más famosa de todas las matemáticas".
- Benjamin Peirce, un matemático del siglo XIX de la Universidad de Harvard, dijo que la identidad "es absolutamente paradójica; no podemos entenderla, y no sabemos lo que significa, pero la hemos demostrado, y por lo tanto sabemos que debe ser la verdad".
En una encuesta de 1990, los lectores de la revista The Mathematical Intelligencer eligieron la identidad de Euler como el teorema más bello de las matemáticas. En otra encuesta de 2004, empató como la "mayor ecuación de la historia".
Se han escrito varios libros para el público general sobre la identidad de Euler, mostrando su importancia y atractivo.
¿Cómo se explica la identidad de Euler?
La identidad de Euler se obtiene de una fórmula más general llamada la Fórmula de Euler. Esta fórmula dice que:
Esta fórmula funciona para cualquier número real x, donde los ángulos de las funciones trigonométricas (seno y coseno) se miden en radianes.
Si en esta fórmula reemplazamos x por el número π, obtenemos:
Sabemos que:
Entonces, al sustituir estos valores en la ecuación, tenemos:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^{i \pi} = -1 + i \cdot 0\,\!

Si sumamos 1 a ambos lados de esta última ecuación, llegamos a la identidad de Euler:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^{i \pi} + 1 = 0 \,\!
¿Cómo se ve la identidad de Euler en un dibujo?
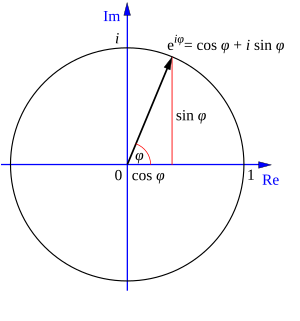
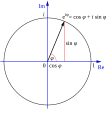
Cualquier número complejo puede representarse como un punto en un plano especial llamado el plano complejo. Este punto se puede describir por su distancia desde el centro (llamada r) y el ángulo que forma con el eje horizontal (llamado θ).
La fórmula de Euler, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): z = r e^{i\theta} , nos dice que un número complejo es como un punto que está a una distancia r del origen y a un ángulo θ.
La identidad de Euler, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): -1 = e^{i\pi} , nos dice algo sobre el número -1 en este plano. Significa que el número -1 está a una distancia de 1 del centro y su ángulo es π radianes (180 grados).
Cuando multiplicas un número complejo por Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^{i\theta} , lo que haces es girar ese número un ángulo de θ en el plano complejo. Como multiplicar por -1 es lo mismo que girar un punto 180 grados alrededor del centro, la identidad de Euler nos muestra que girar un punto π radianes (180 grados) tiene el mismo efecto que multiplicarlo por -1.
Historia de la identidad de Euler
Aunque la identidad de Euler se deriva directamente de la Fórmula de Euler, que fue publicada por Leonhard Euler en 1748, no se sabe con certeza si Euler mismo la escribió exactamente en esta forma tan compacta.
Algunos historiadores de las matemáticas, como Robin Wilson, sugieren que, aunque la identidad se puede deducir fácilmente de los trabajos de otros matemáticos de la época, y Euler seguramente se dio cuenta de ella, no hay evidencia de que la haya escrito explícitamente en sus publicaciones. No se sabe quién fue el primero en presentarla de esta manera.
Ver también
Galería de imágenes
-
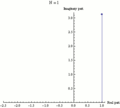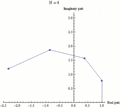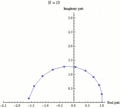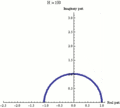
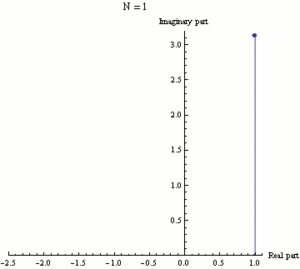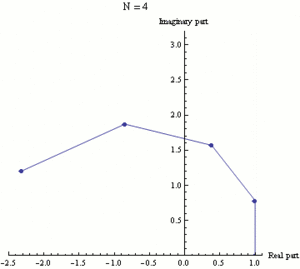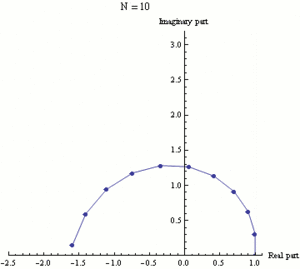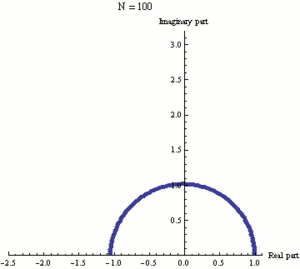
Función exponencial ez puede definirse como el límite de una secuencia (1 + z/N)N, con N tendiendo a infinito, y así e iπ es el límite de (1 + iπ/N)N. Cada fotograma de esta animación muestra números (1 + iπ/N)k', donde k va de 0 a N y N toma varios valores crecientes de 1 a 100.
Véase también
 En inglés: Euler's identity Facts for Kids
En inglés: Euler's identity Facts for Kids