Número real para niños

Enciclopedia para niños

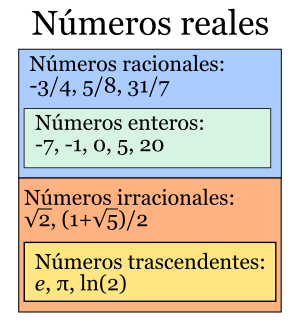
En matemáticas, los números reales (representados con el símbolo R o ℝ) son un conjunto muy importante de números. Incluyen tanto los números racionales (como las fracciones, los números enteros y el cero) como los números irracionales.

Los números irracionales son aquellos que no se pueden escribir como una fracción simple de dos números enteros. Tienen infinitas cifras decimales que no se repiten de forma periódica. Algunos ejemplos famosos son la raíz cuadrada de 5 (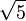 $\sqrt{5}$ ), el número π (pi), y el número real Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \log(2) .

Los números reales se pueden entender y construir de varias maneras. Algunas son más sencillas, pero otras son más complejas y se usan en matemáticas avanzadas para asegurar que todo sea muy preciso.

Durante los siglos XVI y XVII, el cálculo (una rama de las matemáticas) avanzó mucho. Sin embargo, en ese tiempo, no se usaban definiciones tan exactas como las de hoy. Se hablaban de cosas "pequeñas" o "límites" sin una explicación muy precisa. Esto causó algunos problemas y la necesidad de crear una base más sólida para las matemáticas. Así, se crearon definiciones muy exactas para los números reales.

Contenido

¿Qué son los números reales?
- Historia de los números reales
  - El concepto de número a través del tiempo
¿Cómo se escriben los números reales?
Tipos de números reales
- Racionales e irracionales
- Algebraicos y trascendentes
¿Cómo se construyen los números reales?
Operaciones con números reales
- Aproximaciones y errores
Clasificaciones de los números reales
Galería de imágenes
Véase también

¿Qué son los números reales?

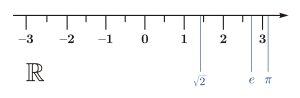
Los números reales son todos los números que puedes encontrar en la recta numérica. Imagina una línea infinita; cada punto en esa línea representa un número real.

Diferentes clases de números reales

Recta real, donde cada punto se relaciona con un número real.

Historia de los números reales

La idea de los números ha evolucionado mucho a lo largo del tiempo.

Los egipcios usaron fracciones hace unos 3000 años.
Alrededor del año 500 a.C., un grupo de matemáticos griegos, liderados por Pitágoras, descubrió que existían números que no podían expresarse como fracciones. A estos los llamamos números irracionales.
Los números negativos aparecieron en la India cerca del año 600. En China también se usaron poco después. En Europa, no se aceptaron completamente hasta el siglo XII.
En el siglo XVIII, el matemático Leonhard Euler aún dudaba de las soluciones negativas de las ecuaciones.
La definición precisa y rigurosa de los números reales, tal como la conocemos hoy, fue establecida por Georg Cantor en 1871.

Muchos matemáticos importantes, desde la antigua Grecia hasta el siglo XIX, como Descartes, Newton, Leibniz, Euler, Lagrange, Gauss, Riemann, Cauchy y Weierstrass, contribuyeron a entender mejor los números reales.

El concepto de número a través del tiempo

Los egipcios y babilonios usaban fracciones para resolver problemas diarios. Pero los pitagóricos en Grecia fueron más allá. Ellos creían que todo en el universo podía explicarse con números enteros y sus proporciones.

Sin embargo, se encontraron con un problema: ¿cómo medir la diagonal de un cuadrado? Si los lados de un cuadrado miden 1, su diagonal mide la raíz cuadrada de dos (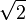 $\sqrt 2$ ). Los pitagóricos descubrieron que 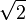$\sqrt 2$ no se podía escribir como una fracción de números enteros. Esto fue un gran descubrimiento y un desafío para su idea de que "todo es número".

Este hallazgo hizo que, durante mucho tiempo, los números irracionales se estudiaran más a través de la geometría (dibujando líneas y figuras) que de la aritmética (cálculos con números). Se les identificaba con puntos en una línea recta.

Con el tiempo, la notación algebraica (usar letras y símbolos para representar números) y el cálculo infinitesimal permitieron manipular estos números de forma más sencilla. Se entendió que un número irracional podía ser el resultado de una suma infinita de números racionales. Por ejemplo, el número pi ( $\pi$ ) se puede calcular con una serie infinita de fracciones.

¿Cómo se escriben los números reales?

Los números reales se escriben con decimales que pueden tener una cantidad infinita de dígitos después de la coma, como 324,823211247... A menudo, se usan tres puntos (...) al final para indicar que hay más dígitos.

En ciencias físicas, las medidas son siempre aproximaciones de un número real. Los ordenadores también solo pueden aproximar los números reales con números racionales. Sin embargo, algunos programas pueden trabajar con números reales de forma exacta usando su definición matemática (por ejemplo, 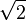$\sqrt{2}$ ) en lugar de su valor decimal aproximado.

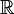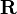Los matemáticos usan el símbolo $\mathbb R$ (o $\mathbf{R}$ ) para representar el conjunto de todos los números reales. La notación 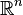$\mathbb R^n$ se refiere a un espacio con "n" dimensiones de números reales. Por ejemplo, 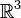$\mathbb R^3$ significa un espacio de tres dimensiones, como el espacio que nos rodea.

La palabra "real" se usa en matemáticas como un adjetivo para indicar que se está trabajando con el conjunto de los números reales. Por ejemplo, una "matriz real" o una "función real".

Tipos de números reales

Los números reales se pueden clasificar de varias maneras.

División gráfica de los números irracionales.

Racionales e irracionales

Un número real puede ser:

Racional: Se puede escribir como una fracción de dos números enteros (por ejemplo, 3/4, -21/3, 5, 0, 1/2). Su representación decimal es periódica (los dígitos se repiten) o finita.

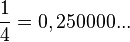* $\frac{1}{4}= 0,250000...$ (es racional, termina en 0s). * 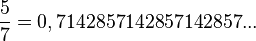$\frac{5}{7}= 0,7142857142857142857...$ (es racional, el grupo "714285" se repite).

Irracional: No se puede escribir como una fracción simple. Su representación decimal es infinita y no periódica (los dígitos no se repiten de forma regular).

* $\frac{\sqrt[3]{7}+1}{2}=1\text{,}456465591386194\ldots$ (es irracional, sus decimales no se repiten).

Los números racionales se representan con 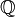$\mathbb{Q}$ y los irracionales con $\mathbb{I}$ .

Algebraicos y trascendentes

Otra forma de clasificar los números reales es en:

Algebraicos: Son aquellos que pueden ser la solución de una ecuación de polinomios con coeficientes racionales. Todos los números racionales son algebraicos. Por ejemplo, si tienes la fracción $\frac{p}{q}$ , es la solución de la ecuación $qx=p$ .

* El número $\frac{\sqrt[3]{7}+1}{2}$ es algebraico porque es una solución de la ecuación Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 4x^3-6x^2+3x-4=0 .

Trascendentes: Son los números reales que no son algebraicos, es decir, no son la solución de ninguna ecuación polinómica con coeficientes racionales.

* Un ejemplo de número trascendente es 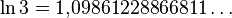$\ln3=1\text{,}09861228866811\ldots$ (el logaritmo natural de 3).

El conjunto de los números algebraicos se representa con 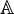$\mathbb{A}$ .

¿Cómo se construyen los números reales?

Existen varias formas de construir los números reales de manera formal en matemáticas.

Construcción por números decimales

Podemos pensar en los números reales como los números decimales que conocemos. Un número decimal se escribe como un número entero seguido de una coma y una secuencia infinita de dígitos (0, 1, 2, ..., 9). Por ejemplo, 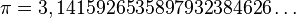$\pi=3,1415926535897932384626\dots$ .

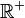Los números decimales con parte entera positiva forman los números reales positivos ( $\mathbb{R}^+$ ).
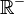Los números decimales con parte entera negativa forman los números reales negativos ( $\mathbb{R}^-$ ).
El número 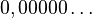$0,00000\dots$ es el cero.

El conjunto de todos los números reales (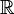 $\mathbb{R}$ ) es la unión de los reales positivos, los reales negativos y el cero.

Construcción por cortes de Dedekind

Esta es una forma más avanzada de definir los números reales. Imagina que tienes todos los números racionales en una línea. Un "corte de Dedekind" divide esta línea en dos grupos:

Un grupo A, con todos los números racionales menores que un cierto valor.
Un grupo B, con todos los números racionales mayores que ese valor.

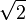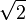El "corte" en sí mismo es el número real que separa esos dos grupos. Por ejemplo, para definir $\sqrt 2$ , el grupo A tendría todos los racionales cuyo cuadrado es menor que 2, y el grupo B tendría todos los racionales cuyo cuadrado es mayor que 2. El "corte" entre ellos es $\sqrt 2$ .

Construcción por sucesiones de Cauchy

Esta construcción usa la idea de "aproximar" un número real con una secuencia de números racionales. Una "sucesión de Cauchy" es una lista infinita de números racionales que se van acercando cada vez más entre sí, como si estuvieran "convergiendo" hacia un punto.

Por ejemplo, el número $\pi$ se puede aproximar con una suma infinita de fracciones. Cada vez que sumas un término más, el resultado se acerca más a $\pi$ . Una sucesión de Cauchy captura esta idea, donde el número real es el "límite" al que se acercan los términos de la sucesión.

Operaciones con números reales

Con los números reales se pueden hacer las operaciones básicas (suma, resta, multiplicación, división), pero hay algunas reglas importantes:

No se pueden calcular raíces de orden par (como la raíz cuadrada o la raíz cuarta) de números negativos dentro de los números reales. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt{-4} no es un número real.
La división entre cero no está definida. No puedes dividir ningún número entre cero.
No se puede calcular el logaritmo de un número real negativo ni de cero.

Estas reglas son importantes en matemáticas. Por ejemplo, al dibujar la gráfica de una función, si hay una división entre cero, la gráfica tendrá un "hueco" o una asíntota (una línea a la que la gráfica se acerca pero nunca toca).

Aproximaciones y errores

Cuando trabajamos con números reales, especialmente con los irracionales, a menudo tenemos que usar aproximaciones con un número limitado de decimales. Esto introduce pequeños errores.

Por ejemplo, para calcular el área de un círculo con 5 metros de radio, usamos la fórmula 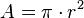$A=\pi\cdot r^2$ . Si usamos $\pi$ con diferentes niveles de precisión, el resultado del área será ligeramente diferente:

Si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \pi \approx 3.1 , el área es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3.1 \cdot 25 = 77.5 m².
Si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \pi \approx 3.14 , el área es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3.14 \cdot 25 = 78.5 m².

Clasificaciones de los números reales

Los números reales se pueden dividir de dos maneras principales:

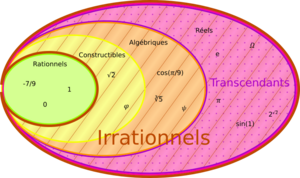
El conjunto de los números reales es la unión de los números racionales y los números irracionales.
El conjunto de los números reales es la unión de los números algebraicos y los números trascendentes.

Todos los números racionales son algebraicos. Los números irracionales pueden ser algebraicos (como 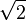$\sqrt{2}$ ) o trascendentes (como $\pi$ ). Todos los números trascendentes son irracionales.

Galería de imágenes

Ojo de Horus o Udyat, que representa un sistema de cuantificación mediante números racionales de las partes de un todo.
Símbolo de los números reales.

Véase también

En inglés: Real number Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Número_real&oldid=5043140»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Número real para Niños. Enciclopedia Kiddle.