Silogismo para niños
El silogismo es un tipo de razonamiento deductivo que forma parte de la lógica. Su origen se remonta a la Antigua Grecia. Un silogismo está compuesto por dos ideas o afirmaciones iniciales, llamadas premisas, y una tercera idea que es la conclusión. Esta conclusión se obtiene de forma lógica y necesaria a partir de las dos premisas.
El silogismo fue creado por Aristóteles, un famoso filósofo griego. Es la idea principal de la lógica aristotélica, que ha sido muy importante para el pensamiento científico y filosófico durante más de dos mil años.
Aristóteles explicó los silogismos en su colección de obras lógicas llamada Órganon, específicamente en los libros conocidos como Primeros Analíticos.

Contenido
- El Silogismo: Un Tipo de Razonamiento Lógico
- Galería de imágenes
- Véase también
El Silogismo: Un Tipo de Razonamiento Lógico
¿Qué es un Silogismo?
Un silogismo es una forma de razonamiento donde, si ciertas ideas son verdaderas, entonces otra idea debe ser verdadera por fuerza. Es como un rompecabezas lógico donde, si tienes dos piezas que encajan, puedes deducir cómo será la tercera pieza.
¿Quién Creó el Silogismo?
El silogismo fue formulado por primera vez por Aristóteles, un filósofo y científico de la Antigua Grecia. Él consideraba la lógica como una forma de conectar diferentes "términos" o conceptos.
Partes de un Silogismo
Según Aristóteles, los silogismos buscan mostrar la relación entre dos ideas principales: un sujeto y un predicado. Estas ideas se unen o se separan en lo que él llamaba "juicios". Para llegar a una conclusión sobre la relación entre el sujeto y el predicado, se comparan con un tercer término, llamado "término medio".
Así, un silogismo tiene dos juicios iniciales, llamados premisa mayor y premisa menor. En estas premisas se comparan tres términos (sujeto, predicado y término medio). De esta comparación, se obtiene un nuevo juicio que es la conclusión.
La lógica de los silogismos busca establecer reglas para asegurar que, si las premisas son verdaderas, la conclusión que se obtiene también sea verdadera.
Las Premisas y la Conclusión
Los elementos principales de un silogismo son:
- Un antecedente: Son las dos ideas iniciales, llamadas premisas.
- Un consecuente: Es la idea final, el juicio que resulta como conclusión.
Los Términos: Sujeto, Predicado y Medio
En un silogismo, usamos tres tipos de términos:
- Un término sujeto (S).
- Un término predicado (P).
- Un término medio (M).
La estructura de un silogismo es la siguiente:
- Premisa mayor: Es el juicio que contiene el término más grande o predicado de la conclusión (P), comparado con el término medio (M).
- Premisa menor: Es el juicio que contiene el término más pequeño o sujeto de la conclusión (S), comparado con el término medio (M).
- Consecuente o conclusión: Es el juicio final al que se llega. Este juicio afirma (une) o niega (separa) la relación entre S y P.
Los juicios que forman las premisas conectan los términos para crear el argumento. De esta manera, el silogismo llega a una conclusión al comparar dos términos con un tercer término.
Tipos de Afirmaciones en los Silogismos
Las afirmaciones (o juicios) en un silogismo se clasifican por su cantidad y su cualidad.
Cantidad: Universal o Particular
La cantidad se refiere a cuántos elementos abarca el término:
- Universal: Cuando el término se refiere a todos los individuos posibles. Por ejemplo, "Todos los estudiantes".
- Particular: Cuando el término se refiere solo a algunos individuos. Por ejemplo, "Algunos estudiantes".
Cualidad: Afirmativa o Negativa
La cualidad se refiere a si la relación entre los términos es de unión o de separación:
- Afirmativa o de unión: El sujeto es el predicado. Por ejemplo, "Los perros son mamíferos".
- Negativa o de separación: El sujeto no es el predicado. Por ejemplo, "Los gatos no son aves".
Combinando cantidad y cualidad, los juicios se clasifican en cuatro tipos, que se representan con las letras A, E, I, O:
| Clase | Nombre | Esquema | Ejemplo | Extensión de los términos |
| A | Universal Afirmativo | Todo S es P | Todos los hombres son mortales | S: Universal P: Particular |
| E | Universal Negativo | Ningún S es P | Ningún hombre es mortal | S: Universal P: Universal |
| I | Particular Afirmativo | Algún S es P | Algún hombre es mortal | S: Particular P: Particular |
| O | Particular Negativo | Algún S no es P | Algún hombre no es mortal | S: Particular P: Universal |
Las letras A e I vienen del verbo latino adfirmo ("afirmo"), y E y O de nego ("niego").
Figuras y Modos del Silogismo
Las figuras del silogismo se refieren a cómo se organizan los términos (S, P, M) en las premisas. Hay cuatro figuras posibles:
| Elemento | 1ª Figura | 2ª Figura | 3ª Figura | 4ª Figura |
| Premisa mayor | M P | P M | M P | P M |
| Premisa menor | S M | S M | M S | M S |
| Conclusión | S P | S P | S P | S P |
Los modos silogísticos son las diferentes combinaciones que se pueden hacer con los tipos de juicios (A, E, I, O) en las dos premisas y la conclusión. Aunque hay 64 combinaciones posibles, solo 19 son válidas si se aplican las reglas del silogismo.
Reglas para un Silogismo Válido
Si se comete un error al construir un silogismo, el resultado es una falacia, es decir, un argumento que parece válido pero no lo es.
Reglas para los Términos
- Un silogismo no puede tener más de tres términos. Esto significa que solo puedes comparar dos ideas con una tercera. Si introduces un cuarto término, el silogismo es incorrecto. Por ejemplo, si usas la palabra "hombre" con dos significados diferentes (como especie y como género masculino), estás introduciendo un cuarto término sin darte cuenta.
- Los términos no deben ser más amplios en la conclusión que en las premisas. La conclusión solo puede hablar de lo que ya se comparó en las premisas.
- El término medio no puede aparecer en la conclusión. La función del término medio es solo conectar las otras dos ideas. Una vez que la conexión se establece, ya no es necesario en la conclusión.
- El término medio debe ser universal en al menos una de las premisas. Para que la comparación sea correcta, el término medio debe ser considerado en su totalidad al menos una vez. Si no, podría ser que se comparen solo partes diferentes del término medio, lo que llevaría a un error.
Reglas para las Afirmaciones (Proposiciones)
- De dos premisas negativas no se puede obtener ninguna conclusión. Si ambas premisas niegan algo, no hay forma de saber qué relación existe entre el sujeto y el predicado. Al menos una premisa debe ser afirmativa.
- De dos premisas afirmativas no se puede sacar una conclusión negativa. Si ambas premisas afirman una relación, la conclusión también debe ser afirmativa.
- La conclusión siempre sigue la parte más débil. Esto significa que si hay una premisa negativa, la conclusión será negativa. Si hay una premisa particular, la conclusión será particular.
- De dos premisas particulares no se obtiene una conclusión válida. Si ambas premisas son particulares (usan "algunos"), no hay suficiente información para sacar una conclusión segura.
Modos Válidos
Los modos válidos son las combinaciones específicas de tipos de juicios (A, E, I, O) que, al seguir las reglas, producen silogismos correctos. De las 64 combinaciones posibles, solo 19 son válidas. Tradicionalmente, se les daban nombres latinos para memorizarlos:
| Modos Válidos | Nombres para memorizar | |
| De la primera figura | AAA, EAE, AII, EIO | BARBARA, CELARENT, DARII, FERIO |
| De la segunda figura | EAE, AEE, EIO, AOO | CESARE, CAMESTRES, FESTINO, BAROCO |
| De la tercera figura | AAI, IAI, AII, EAO, OAO, EIO | DARAPTI, DISAMIS, DATISI, FELAPTON, FERISON, BOCARDO |
| De la cuarta figura | AAI, AEE, IAI, EAO, EIO | BAMALIP, CAMENES, DIMARIS, FRESISON, FESAPO |
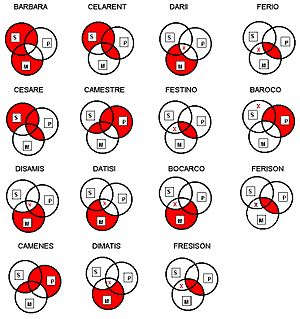
Representación Gráfica de los Modos con Diagramas de Venn
Los silogismos se pueden representar visualmente usando diagramas de Venn.
En estos diagramas:
- Cada término (S, P, M) se representa con un círculo.
- Las áreas sombreadas indican que no hay elementos en esa parte.
- Una "X" indica que al menos un elemento existe en esa área.
- La conclusión se ve al observar la relación entre los círculos S y P después de considerar el círculo M.
¿Por Qué es Importante el Silogismo?
El silogismo de Aristóteles fue un pilar fundamental para el desarrollo del pensamiento lógico. Aunque la lógica moderna es más compleja y usa símbolos para representar las ideas, el silogismo sigue siendo la base de cómo entendemos el razonamiento deductivo.
La lógica moderna, por ejemplo, interpreta un silogismo como una relación entre "clases" o "conjuntos" de cosas. Por ejemplo, el silogismo "Todos los hombres son mortales. Todos los griegos son hombres. Por lo tanto, todos los griegos son mortales" se puede ver como: "Si el conjunto de los griegos está dentro del conjunto de los hombres, y el conjunto de los hombres está dentro del conjunto de los mortales, entonces el conjunto de los griegos está dentro del conjunto de los mortales".
Esto muestra cómo las ideas de Aristóteles, aunque antiguas, siguen siendo la base para entender cómo funciona la lógica y el razonamiento en la actualidad.
Galería de imágenes
-
Aristóteles. Museo del Louvre.
Véase también
 En inglés: Syllogism Facts for Kids
En inglés: Syllogism Facts for Kids