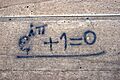Fórmula de Euler para niños
La fórmula de Euler o relación de Euler es una idea muy importante en las matemáticas, nombrada en honor al famoso matemático Leonhard Euler. Esta fórmula nos muestra una conexión fundamental entre las funciones trigonométricas (como el seno y el coseno) y la función exponencial cuando trabajamos con números complejos.
La fórmula de Euler dice que para cualquier número real x (que podemos pensar como un ángulo medido en radianes):
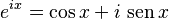
Aquí, e es la base del logaritmo natural (un número especial que vale aproximadamente 2.718), i es la unidad imaginaria (que es la raíz cuadrada de -1, es decir, 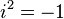 ), y
), y 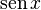 y
y 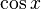 son las funciones trigonométricas seno y coseno.
son las funciones trigonométricas seno y coseno.
Esta fórmula es tan importante que el físico Richard Feynman la llamó "nuestra joya" y "la fórmula más notable de las matemáticas". Se usa muchísimo en matemáticas, física, química e ingeniería.
Cuando el valor de x es el número pi (π, aproximadamente 3.14159), la fórmula de Euler se convierte en una expresión aún más famosa, conocida como la identidad de Euler:
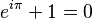
Esta identidad es especial porque conecta cinco de los números más importantes en matemáticas: e, i, π, 1 y 0.
Contenido
¿Quién Descubrió y Popularizó la Fórmula de Euler?
Aunque la fórmula lleva el nombre de Leonhard Euler, la idea de conectar las funciones trigonométricas con los logaritmos (que están relacionados con las exponenciales) ya había sido explorada antes.
Los Primeros Pasos
Un matemático llamado Roger Cotes descubrió una relación similar en 1714. Él la publicó en una obra póstuma en 1722. Sin embargo, su trabajo usaba logaritmos en lugar de la función exponencial directamente.
La Contribución de Euler
Fue Leonhard Euler quien desarrolló la fórmula usando la función exponencial, como la conocemos hoy. Él la compartió en una carta en 1741 y la publicó y popularizó en su importante libro Introductio in analysin infinitorum en 1748. Gracias a Euler, esta fórmula se hizo muy conocida y estudiada.
Visualizando los Números Complejos
Es interesante saber que ni Cotes ni Euler vieron los números complejos como puntos en un plano, como los dibujamos hoy. Esa forma de entenderlos surgió más tarde, en 1787, gracias al matemático Caspar Wessel. Esto ayudó mucho a visualizar y comprender mejor la fórmula de Euler.
¿Por Qué es Importante la Fórmula de Euler?
La fórmula de Euler es una herramienta muy poderosa en matemáticas y tiene muchas aplicaciones.
Uniendo Ramas de las Matemáticas
Esta fórmula crea un puente entre el análisis matemático (que estudia funciones, límites y cambios) y la trigonometría (que estudia los ángulos y las formas). Permite representar los números complejos de una manera diferente, usando lo que se llama coordenadas polares.
Calculando con Números Negativos y Complejos
La fórmula de Euler nos ayuda a entender cómo funcionan los logaritmos de números negativos y números complejos. Por ejemplo, si usamos la identidad de Euler ( ), podemos ver que el logaritmo natural de -1 es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): i\pi . Esto abre un mundo de posibilidades para trabajar con números que antes parecían imposibles de calcular con logaritmos.
), podemos ver que el logaritmo natural de -1 es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): i\pi . Esto abre un mundo de posibilidades para trabajar con números que antes parecían imposibles de calcular con logaritmos.
Simplificando Cálculos Complejos
Una de las grandes ventajas de la fórmula de Euler es que simplifica mucho las operaciones de cálculo, como la derivación y la integración. Las funciones exponenciales son más fáciles de manejar en estos cálculos que las funciones trigonométricas, y la fórmula de Euler nos permite convertir unas en otras. Esto es muy útil para resolver ecuaciones diferenciales, que son ecuaciones que describen cómo cambian las cosas.
Relación con las Funciones Trigonométricas
La fórmula de Euler también nos permite ver las funciones seno y coseno como partes de la función exponencial compleja. Esto significa que podemos definir el seno y el coseno para números complejos, no solo para números reales.
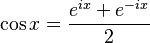
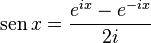
Estas definiciones son muy útiles y mantienen las mismas propiedades que las funciones seno y coseno que ya conoces.
¿Cómo se Demuestra la Fórmula de Euler?
La fórmula de Euler se puede demostrar de varias maneras. Una forma común es usando las series de Taylor, que son formas de escribir funciones como sumas infinitas de términos.
Demostración con Series de Taylor
Las funciones 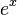 ,
, 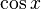 y
y 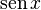 se pueden escribir como series de Taylor:
se pueden escribir como series de Taylor:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \cdots
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots
Si reemplazamos x por ix en la serie de 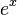 y recordamos que
y recordamos que 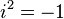 ,
,  ,
,  , etc., podemos reordenar los términos y ver que se separan en la serie del coseno y la serie del seno, ¡demostrando así la fórmula de Euler!
, etc., podemos reordenar los términos y ver que se separan en la serie del coseno y la serie del seno, ¡demostrando así la fórmula de Euler!
Aplicaciones de la Fórmula de Euler
La fórmula de Euler tiene muchas aplicaciones prácticas.
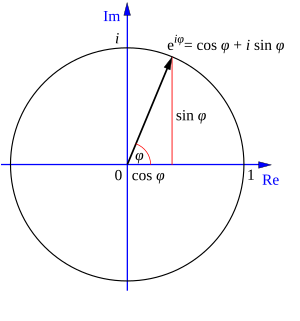
Interpretación Geométrica
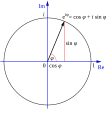
Podemos pensar en la función 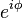 como un punto que se mueve en un círculo unitario (un círculo con radio 1) en el plano complejo. A medida que el ángulo
como un punto que se mueve en un círculo unitario (un círculo con radio 1) en el plano complejo. A medida que el ángulo 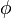 cambia, el punto se mueve alrededor del círculo. El valor de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cos \phi nos da la posición horizontal (eje real) y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sen \phi nos da la posición vertical (eje imaginario) de ese punto.
cambia, el punto se mueve alrededor del círculo. El valor de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cos \phi nos da la posición horizontal (eje real) y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sen \phi nos da la posición vertical (eje imaginario) de ese punto.
Esto es muy útil para entender y trabajar con números complejos en coordenadas polares, lo que simplifica mucho las multiplicaciones y potencias de estos números.
Galería de imágenes
-
La fórmula de Euler ilustrada en el plano complejo.
Véase también
 En inglés: Euler's formula Facts for Kids
En inglés: Euler's formula Facts for Kids