Función inversa para niños
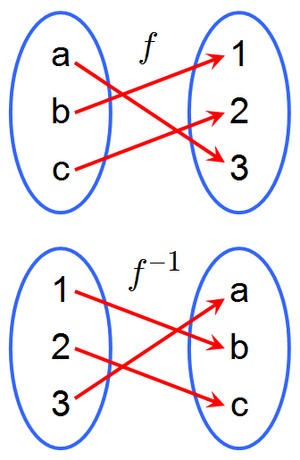
En matemáticas, especialmente en el estudio de las funciones, si tienes una función f que toma un valor de un grupo (llamado dominio) y lo transforma en un valor de otro grupo (llamado imagen), a veces es posible encontrar otra función que haga el camino inverso. Esta función "de vuelta" se llama función inversa de f, y se escribe como f -1. Piensa en ella como la función que "deshace" lo que hizo la función original.
Por ejemplo, si la función f toma el número 2 y lo convierte en 4 (como en f(x) = x + 2), su función inversa tomaría el 4 y lo convertiría de nuevo en 2 (como en f⁻¹(y) = y - 2).
Contenido
¿Qué es una Función Inversa?
Una función inversa es como el "opuesto" de una función original. Si una función f toma un número x y te da un resultado y (es decir, f(x) = y), entonces su función inversa, f⁻¹, tomará ese resultado y y te devolverá el número original x (es decir, f⁻¹(y) = x).
Para que una función tenga una inversa, debe cumplir una condición especial: cada valor de entrada debe tener una salida única, y cada salida debe provenir de una entrada única. Esto se conoce como ser una función biyectiva. Si una función no es biyectiva, no puede tener una función inversa que funcione para todos sus valores.
¿Cómo se relacionan las funciones y sus inversas?
Las funciones y sus inversas tienen una relación muy especial. Si aplicas una función y luego su inversa (o viceversa), es como si no hubieras hecho nada. El resultado es el valor original.
- Si aplicas la función inversa f⁻¹ a lo que te dio la función f, obtienes el valor original.
- Si aplicas la función f a lo que te dio la función inversa f⁻¹, también obtienes el valor original.
Esto se puede ver con la idea de "identidad", que significa que el valor no cambia.
Nombres diferentes para la función inversa
Aunque f⁻¹ es la forma más común de escribir una función inversa, a veces se usan otras notaciones para evitar confusiones. Por ejemplo, en algunos campos de las matemáticas, podrías ver una estrella (f*) o un signo menos (f⁻) para indicar la función inversa. Sin embargo, f⁻¹ es la más reconocida.
Propiedades de las Funciones Inversas
Las funciones inversas tienen algunas propiedades interesantes que las hacen muy útiles en matemáticas.
Invertir el orden de las funciones
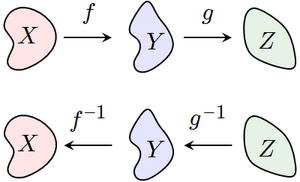
Si tienes dos funciones, f y g, y las aplicas una después de la otra (esto se llama "composición de funciones"), y luego quieres encontrar la inversa de esa combinación, el orden de las inversas se invierte.
Por ejemplo, si primero aplicas f y luego g (escrito como g o f), para "deshacer" eso, primero tienes que deshacer g con g⁻¹, y luego deshacer f con f⁻¹. Así, la inversa de (g o f) es (f⁻¹ o g⁻¹).
La inversa de la inversa
Una propiedad muy sencilla es que si tomas la función inversa de una función inversa, ¡vuelves a la función original! Es como decir "deshacer lo deshecho". Si tienes f⁻¹, y le aplicas su propia inversa, el resultado es f.
Gráficas de las Funciones Inversas
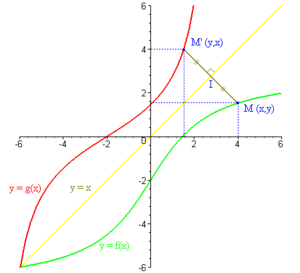
Cuando dibujas la gráfica de una función y la de su inversa en un plano de coordenadas, notarás algo muy interesante: son simétricas.
- Si doblas el papel por la línea recta y = x (que es la diagonal que va desde la esquina inferior izquierda a la superior derecha), las dos gráficas coincidirán perfectamente.
- Esto sucede porque si un punto (x, y) está en la gráfica de f, entonces el punto (y, x) estará en la gráfica de f⁻¹. Es como si los valores de x e y simplemente intercambiaran sus lugares.
Ejemplos de Funciones Inversas
Las funciones inversas aparecen en muchos lugares en las matemáticas. Aquí tienes algunos ejemplos comunes:
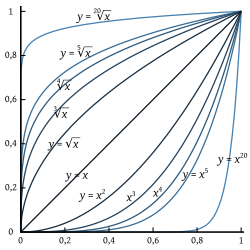
- Raíz cuadrada y Potencia al cuadrado: La función que eleva un número al cuadrado (x²) tiene como inversa a la función raíz cuadrada (√x), siempre y cuando trabajemos con números positivos. Si tomas un número positivo, lo elevas al cuadrado y luego le sacas la raíz cuadrada, obtienes el número original.
- Raíz enésima y Potencia enésima: De manera similar, la función que eleva un número a la potencia n (xⁿ) tiene como inversa a la función raíz enésima (ⁿ√x).
- Exponencial y Logaritmo: La función exponencial (como eˣ) y la función logaritmo natural (ln x) son inversas entre sí. Una "deshace" lo que hace la otra.
- Funciones trigonométricas inversas: Las funciones como el seno, coseno y tangente tienen sus propias funciones inversas, llamadas arcoseno (arcsen), arcocoseno (arccos) y arcotangente (arctan). Estas funciones te permiten encontrar el ángulo si conoces el valor del seno, coseno o tangente.
Véase también
 En inglés: Inverse function Facts for Kids
En inglés: Inverse function Facts for Kids
- Teorema de la función inversa, que explica cuándo una función inversa existe y es "suave" (continua y diferenciable).