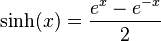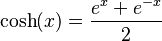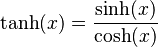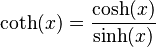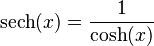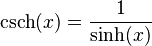Función hiperbólica para niños

Las funciones hiperbólicas son un tipo especial de funciones matemáticas que se parecen mucho a las funciones trigonométricas que ya conoces, como el seno y el coseno. Sin embargo, en lugar de estar relacionadas con un círculo, estas funciones están conectadas con una figura geométrica llamada hipérbola.

Así como los puntos de un círculo se pueden describir con el seno y el coseno, los puntos de una hipérbola se pueden describir con las funciones hiperbólicas. Son muy útiles en diferentes áreas de las matemáticas y la física, como en el estudio de curvas especiales como la catenaria (la forma que toma un cable colgando libremente) o en la teoría electromagnética.

¿Qué son las funciones hiperbólicas principales?

Las funciones hiperbólicas se definen a partir de la función exponencial, que es una función matemática muy importante. Las más conocidas son:

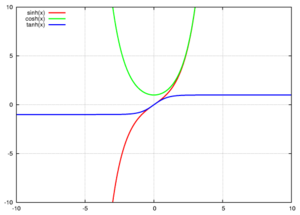
• Seno hiperbólico (se escribe como "sinh")
• Coseno hiperbólico (se escribe como "cosh")

A partir de estas dos, se derivan otras funciones, similares a cómo la tangente se deriva del seno y el coseno:

• Tangente hiperbólica (se escribe como "tanh")
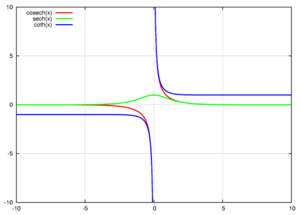
• Cosecante hiperbólica (se escribe como "csch" o "cosech")
• Secante hiperbólica (se escribe como "sech")
• Cotangente hiperbólica (se escribe como "coth")

¿Cómo se calculan estas funciones?

Las funciones hiperbólicas se definen usando la función exponencial (representada por e elevado a una potencia). Aquí te mostramos sus fórmulas básicas:

• El seno hiperbólico de un número x se calcula así:

• El coseno hiperbólico de un número x se calcula así:

• La tangente hiperbólica se obtiene dividiendo el seno hiperbólico entre el coseno hiperbólico:

Las otras funciones se definen de manera similar, como inversas o divisiones de las anteriores:

• La cotangente hiperbólica:

• La secante hiperbólica:

• La cosecante hiperbólica:

Curvas de las funciones hiperbólicas sinh, cosh y tanh

Curvas de las funciones hiperbólicas csch, sech y coth

¿Para qué se usan las funciones hiperbólicas?

Las funciones hiperbólicas son muy importantes en varias áreas:

• Geometría hiperbólica: Se utilizan para calcular ángulos y distancias en un tipo de geometría diferente a la que conocemos, donde las reglas de las líneas y las formas son distintas.
• Ecuaciones diferenciales: Ayudan a resolver muchos problemas en física e ingeniería que se describen con ecuaciones especiales, como la que define la forma de una catenaria (un cable o cadena colgando entre dos puntos).
• Física: Aparecen en campos como la teoría electromagnética, la transferencia de calor, el movimiento de fluidos y la relatividad especial.

¿Cómo se relacionan con las funciones trigonométricas?

Las funciones trigonométricas (seno, coseno) se relacionan con un círculo unitario (un círculo con radio 1). Si tomas un punto en este círculo, sus coordenadas (x, y) pueden ser (cos t, sen t), donde t es un ángulo.

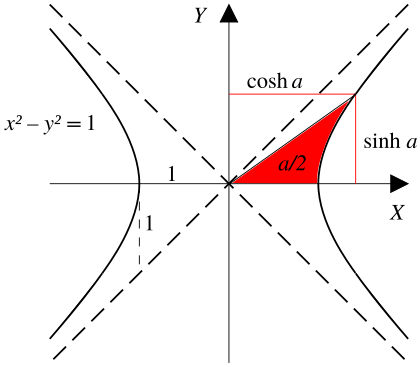
De manera similar, las funciones hiperbólicas (cosh, sinh) se relacionan con una hipérbola unitaria (una hipérbola especial). Los puntos de la mitad derecha de esta hipérbola se pueden describir como (cosh t, sinh t).

Una diferencia interesante es cómo cambian estas funciones. La derivada de sen(t) es cos(t), y la de cos(t) es -sen(t). En cambio, la derivada de sinh(t) es cosh(t), y la de cosh(t) es ¡+sinh(t)! Esto las hace únicas.

Un rayo a través de la hipérbola unitaria x² - y² = 1 en el punto (cosh a, sinh a). El valor a es el doble del área entre el rayo, la hipérbola y el eje x.

Animación de la representación del seno hiperbólico.

Historia de las funciones hiperbólicas

Las funciones hiperbólicas fueron estudiadas por primera vez en la década de 1760 por dos matemáticos, Vincenzo Riccati y Johann Heinrich Lambert, cada uno por su cuenta. Riccati usó las abreviaturas Sh. y Ch. para seno y coseno hiperbólico, mientras que Lambert adoptó los nombres pero cambió las abreviaturas a las que usamos hoy en día: sinh y cosh.

Funciones hiperbólicas inversas

Así como existen funciones inversas para las operaciones matemáticas (como la resta es la inversa de la suma), también existen funciones inversas para las funciones hiperbólicas. Estas se llaman funciones hiperbólicas inversas. Por ejemplo, si tienes un valor de seno hiperbólico, la función inversa te dirá cuál fue el "ángulo hiperbólico" que lo produjo.

Se les suele llamar "seno hiperbólico de área" (arsinh o sinh^-1), "coseno hiperbólico de área" (arcosh o cosh^-1), y así sucesivamente para las demás.

Galería de imágenes

• 

  Curvas de las funciones hiperbólicas

• 

  Curvas de las funciones hiperbólicas

• 

  Un rayo a través de la hipérbola unitaria x² - y^{2 = 1 en el punto (cosh a, sinh a). El valor a es el doble del área entre el rayo, la hipérbola y el eje x.}

• 

  ^{Animación de la representación del seno hiperbólico.}

^{Véase también}

^{En inglés: Hyperbolic functions Facts for Kids}