Diagrama de Venn para niños
Los diagramas de Venn son dibujos que nos ayudan a entender cómo se relacionan diferentes grupos de cosas, llamados conjuntos. Se usan mucho en matemáticas, lógica y para resolver problemas. Estos diagramas muestran los conjuntos usando líneas cerradas, como círculos u óvalos. La línea más grande que los rodea a todos representa el conjunto universal, que incluye todo lo que estamos estudiando.
Estos diagramas fueron creados alrededor de 1880 por un matemático llamado John Venn.
Contenido
- ¿Qué son los diagramas de Venn y para qué sirven?
- ¿Quién inventó los diagramas de Venn?
- Tipos de diagramas de Venn: con elementos o conceptos
- ¿Cuántas regiones tienen los diagramas de Venn?
- ¿Qué otras representaciones se parecen a los diagramas de Venn?
- ¿Para qué se usan los diagramas de Venn en la vida real?
- Galería de imágenes
- Véase también
¿Qué son los diagramas de Venn y para qué sirven?
Los diagramas de Venn nos permiten ver cómo se conectan los conjuntos. Podemos mostrar si tienen elementos en común (intersección), si un conjunto está dentro de otro (inclusión) o si no tienen nada en común (disyunción). Todo esto se ve sin cambiar la posición de los círculos.
¿Cómo se muestra la intersección en un diagrama de Venn?
Cuando dos conjuntos tienen elementos que son iguales, las áreas de sus círculos se superponen. Los elementos que están en esa zona donde se cruzan pertenecen a ambos conjuntos al mismo tiempo. A esa parte se le llama la intersección.
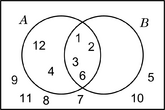
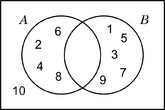
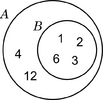
| A = {1; 2; 3; 4; 6; 12} B = {1; 3; 5; 15} U = {1; 2; 3; 4; 5; 6; 12; 15} |
 |
| A = {x | x es divisor natural de 12} B = {x | x es divisor natural de 15} U = {x | x es natural menor o igual que 15} |
 |
En este ejemplo, la intersección de A y B es {1, 3}.
¿Cómo se representa la inclusión en un diagrama de Venn?
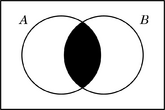
Si todos los elementos de un conjunto también están dentro de otro conjunto, decimos que el primer conjunto es un subconjunto del segundo, o que está incluido en él. En los diagramas de Venn, esto se muestra dibujando un círculo completamente dentro de otro. Si una parte del diagrama no tiene elementos, se suele colorear de un modo diferente para indicarlo.
| A = {1; 2; 3; 4; 6; 12} B = {1; 2; 3; 6} U = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12} |
 |
| A = {x | x es divisor natural de 12} B = {x | x es divisor natural de 6} U = {x | x es natural menor o igual que 12} |
 |
¿Qué significa la disyunción en un diagrama de Venn?
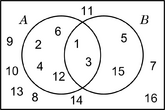
Cuando dos conjuntos no tienen ningún elemento en común, se dice que son disjuntos. En un diagrama de Venn, esto se ve cuando los círculos no se tocan ni se superponen. La zona donde se cruzarían queda vacía.
| A = {2; 4; 6; 8} B = {1; 3; 5; 7; 9} U = {1; 2; 3; 4; 5; 6; 7; 8; 9} |
 |
| A = {x | x es par y de una cifra} B = {x | x es impar y de una cifra} U = {x | x es natural menor que 10} |
 |
A la izquierda de los diagramas, los conjuntos se definen de dos maneras: listando sus elementos o describiendo una característica común.
¿Quién inventó los diagramas de Venn?
Los diagramas de Venn llevan el nombre de su creador, John Venn, un matemático y filósofo de Gran Bretaña. Él estudió y luego enseñó en el Caius College de la Universidad de Cambridge. Allí desarrolló todas sus ideas.
Los diagramas que usamos hoy fueron presentados en julio de 1880 en un trabajo que se hizo muy famoso en el mundo de la lógica. Antes de Venn, otros pensadores como Gottfried Leibniz y Leonhard Euler también usaron dibujos para representar ideas lógicas. Los diagramas de Euler son parecidos, pero no muestran las regiones vacías ni el conjunto universal.
 |
| Diagrama de Euler |
Los diagramas de Venn se volvieron el estándar para representar operaciones lógicas. El concepto de "conjunto universal" se le atribuye a Charles Dodgson, más conocido como Lewis Carroll, el autor de cuentos para niños.
El primer registro escrito de la frase "diagrama de Venn" es de 1918, en un libro de Clarence Irving Lewis.
Tipos de diagramas de Venn: con elementos o conceptos
Los diagramas de Venn pueden mostrar elementos específicos o ideas más generales. Hay dos tipos principales:
- Los que muestran elementos dentro de las líneas cerradas.
- Los que representan solo ideas o conceptos. Estos últimos son más útiles para pensar de forma abstracta y llegar a conclusiones más amplias.
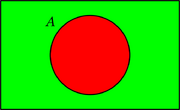
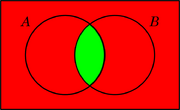
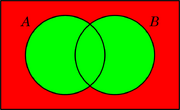
Los siguientes diagramas muestran cuatro operaciones básicas con conjuntos usando un código de dos colores (como un semáforo).
 |
 |
 |
 |
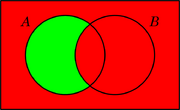| ¬A (No A) | A ∧ B (A y B) | A ∨ B (A o B) | A – B (A menos B) |
Con las dos primeras operaciones (negación y conjunción), se pueden crear las otras dos (disyunción y sustracción). Los colores se pueden interpretar como números binarios (rojo = 0, verde = 1), convirtiendo las operaciones con conjuntos en operaciones con números.
¿Cuántas regiones tienen los diagramas de Venn?
La cantidad de regiones en un diagrama de Venn depende de cuántos conjuntos se estén comparando.
 |
 |
 |
| 1 conjunto (2 regiones) | 2 conjuntos (4 regiones) | 3 conjuntos (8 regiones) |
El color gris en los diagramas representa los elementos que no pertenecen a ninguno de los conjuntos definidos.
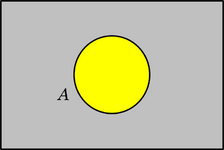
Diagrama de un conjunto
Este diagrama tiene solo 2 regiones: una para los elementos que cumplen la característica del conjunto A, y otra para los que no la cumplen.
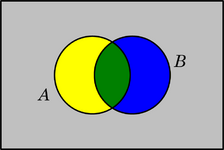
Diagrama de dos conjuntos
Este diagrama tiene 4 regiones. Por ejemplo, si el conjunto A son los animales con dos patas y el conjunto B son los animales que pueden volar:
- A (regiones amarilla y verde): animales con dos patas.
- B (regiones azul y verde): animales que pueden volar.
- A y B (región verde): animales con dos patas que pueden volar (como los loros).
- A y no B (región amarilla): animales con dos patas que no pueden volar (como los pingüinos).
- No A y B (región azul): animales sin dos patas que pueden volar (como los mosquitos).
- No A y no B (región gris): animales sin dos patas que no pueden volar (como las ballenas).
- A o B (regiones amarilla, azul y verde): animales con dos patas o que pueden volar.
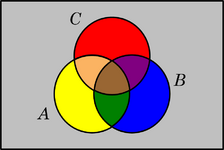
Diagrama de tres conjuntos
Estos diagramas tienen 8 regiones. John Venn los usó mucho. Un ejemplo podría ser: un grupo de personas, donde A son las personas de género masculino, B son las mayores de 18 años y C son las que trabajan. La región verde, por ejemplo, representaría a las personas de género masculino, mayores de 18 años, que no trabajan.
Diagramas con más de tres conjuntos
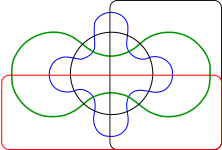
Representar más de tres conjuntos es más difícil. Venn disfrutaba diseñando estos diagramas complejos. Creó varias formas usando elipses y dio ideas para construir diagramas con muchas curvas.
Diagramas de Edwards
Anthony William Fairbank Edwards propuso diagramas para más de tres conjuntos. Los imaginó proyectados sobre una esfera. Luego, estos se pueden dibujar en un plano, pareciendo engranajes con muchos dientes. Edwards los ideó mientras diseñaba un vitral en honor a Venn en el Caius College.
 |
 |
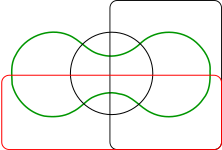| 3 conjuntos | 4 conjuntos |
 |
 |
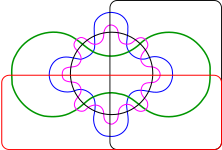| 5 conjuntos | 6 conjuntos |
Otros tipos de diagramas
Otros matemáticos como Branko Grünbaum y Phillip Smith también crearon diagramas para muchos conjuntos. Lewis Carroll diseñó un diagrama para cinco conjuntos.
¿Qué otras representaciones se parecen a los diagramas de Venn?
Existen otras formas de representar ideas lógicas que se relacionan con los diagramas de Venn.
Líneas de Leibniz
Fueron las primeras representaciones de conceptos lógicos. Aunque Leibniz también usó círculos, prefería las líneas.
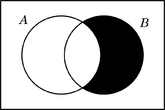
Círculos de Euler
Los círculos de Euler son anteriores a los diagramas de Venn y todavía se usan en algunas ocasiones. La principal diferencia es que los diagramas de Euler no muestran las regiones vacías y no representan el conjunto universal.
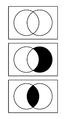
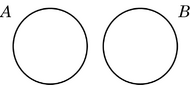
| Inclusión | Disyunción | |
| Leibniz |  |
 |
| Euler |  |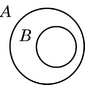
 |
| Venn |  |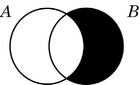
 |
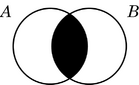Los diagramas de Venn muestran la relación entre los conjuntos sin moverlos, pero añaden la regla de sombrear las regiones que están vacías.
Mapas de Karnaugh
Los mapas de Karnaugh son una forma visual de representar expresiones del álgebra de Boole, que es un tipo de lógica matemática.
Gráficos de Peirce
Los gráficos de Charles Sanders Peirce son una extensión de los diagramas de Venn que incluyen más tipos de información, como afirmaciones de existencia o de probabilidad.
¿Para qué se usan los diagramas de Venn en la vida real?
Los diagramas de Venn son muy útiles en muchas áreas, como las matemáticas, la estadística, la lógica y la informática. Aquí te mostramos algunas de sus aplicaciones más comunes:
Aplicaciones generales
- Análisis de datos: Ayudan a analizar datos y encontrar patrones en grandes grupos de información. Por ejemplo, para comparar los resultados de diferentes encuestas.
- Probabilidad: Se usan en la teoría de la probabilidad para representar eventos y cómo se superponen. Por ejemplo, para visualizar la probabilidad de que algo ocurra si ya ha ocurrido otra cosa.
- Lógica: Son comunes en la lógica para representar ideas y sus relaciones. Por ejemplo, para mostrar la relación entre "todos los perros son mamíferos" y "todos los mamíferos tienen pelo".
- Estadística: Sirven para mostrar relaciones entre diferentes grupos de datos. Por ejemplo, para ver la intersección entre pacientes que recibieron distintos tratamientos.
- Informática: En la informática, se usan para visualizar relaciones entre conjuntos de datos en bases de datos y algoritmos de búsqueda. Por ejemplo, para ver cómo se relacionan los datos en diferentes tablas de una base de datos.
En el trabajo
- Análisis de habilidades: Ayudan a identificar las habilidades necesarias para un puesto. Se pueden dibujar círculos para habilidades como liderazgo o experiencia en ventas, y la intersección muestra las habilidades clave.
- Roles y responsabilidades: Permiten visualizar las tareas de los miembros de un equipo. Los círculos pueden representar roles (gerente, diseñador) y las superposiciones muestran responsabilidades compartidas.
- Identificación de problemas: Se usan para encontrar las causas de un problema en un equipo o proyecto. Los círculos pueden ser áreas como presupuesto o personal, y las superposiciones muestran dónde se juntan los problemas.
- Planificación de proyectos: Ayudan a planificar y visualizar las etapas de un proyecto. Los círculos pueden ser fases (investigación, planificación) y las superposiciones muestran cómo se conectan.
En la educación
- Enseñanza de conjuntos: Son una herramienta excelente para enseñar la teoría de conjuntos, ya que permiten ver la relación entre diferentes conjuntos y sus elementos.
- Comparación de temas: Se usan para comparar y contrastar diferentes temas o conceptos. Por ejemplo, para ver similitudes y diferencias entre periodos históricos.
- Identificación de ideas clave: Ayudan a identificar los conceptos más importantes en un texto o tema. Los estudiantes pueden ver dónde se superponen las ideas principales.
- Análisis de datos: Se utilizan para analizar y visualizar datos en estadística y matemáticas. Por ejemplo, para mostrar la relación entre diferentes categorías de datos.
- Desarrollo del pensamiento crítico: Fomentan el pensamiento crítico al hacer que los estudiantes comparen y contrasten ideas para llegar a conclusiones más informadas.
Galería de imágenes
-
Diagramas de Venn que corresponden respectivamente a las relaciones topológicas de unión, inclusión y disyunción entre dos conjuntos
Véase también
En inglés: Venn diagram Facts for Kids
- Diagramas
- Teoría de conjuntos
- Círculos de Euler
- Mapas de Karnaugh
- Cartas de Smith
- Diagramas de Carroll
- Gráficos existenciales
- Razonamiento diagramático
- Álgebra de Boole
- Vesica piscis
