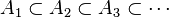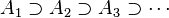Emmy Noether para niños

Datos para niños Emmy Noether
Amalie Emmy Noether
Información personal
Nombre de nacimiento	Amalie Emmy Noether
Nacimiento	23 de marzo de 1882 Erlangen, Baviera, Alemania
Fallecimiento	14 de abril de 1935 (53 años) Bryn Mawr (Pensilvania, Estados Unidos)
Causa de muerte	Quiste ovárico
Sepultura	Old Library
Nacionalidad	Alemana (1882-1933) Estadounidense (1933-35)
Familia
Padres	Ida Amalia Kaufmann Max Noether
Educación
Educación	doctorado y habilitación universitaria
Educada en	Universidad de Erlangen-Núremberg
Supervisor doctoral	Paul Gordan
Información profesional
Área	Matemáticas y física
Conocida por	Álgebra abstracta, física teórica, Teorema de Noether
Empleador	Universidad de Gotinga Bryn Mawr College
Estudiantes doctorales	Max Deuring Hans Fitting Grete Hermann Zeng Jiongzhi Hans Reichenbach
Alumnos	Bartel Leendert van der Waerden
Obras notables	teorema de Noether
Partido político	Partido Socialdemócrata Independiente de Alemania (1919-1922) Partido Socialdemócrata de Alemania (1922-1924)
Miembro de	Deutsche Mathematiker-Vereinigung (desde 1909)
Distinciones	Ackermann-Teubner-Gedächtnispreis (1932)

Amalie Emmy Noether (pronunciado en alemán [ˈnøːtɐ]; Erlangen, Baviera, Alemania, 23 de marzo de 1882 - Bryn Mawr, Pensilvania, Estados Unidos, 14 de abril de 1935) fue una matemática alemana, de ascendencia judía, especialista en la teoría de invariantes y conocida por sus contribuciones de fundamental importancia en los campos de la física teórica y el álgebra abstracta. Considerada por David Hilbert, Albert Einstein y otros personajes como la mujer más importante en la historia de la matemática, revolucionó la teoría de anillos, teoría de cuerpos y la de K-álgebras. En física, el teorema de Noether explica la conexión fundamental entre la simetría en física y las leyes de conservación. A pesar de ello, se le negó la posibilidad de un puesto digno en la universidad por el hecho de ser mujer.

Trayectoria vital

Emmy Noether nació en una familia judía en la ciudad bávara de Erlangen; su padre era el matemático Max Noether, descendiente de una familia de comerciantes al por mayor de Alemania. El padre, en gran medida autodidacta, recibió el doctorado de la Universidad de Heidelberg en 1868, y tras desempeñar su labor docente durante siete años, obtuvo un puesto en la ciudad bávara de Erlangen, donde conoció y posteriormente se casó con Ida Amalia Kaufmann; madre de Emmy.

Emmy Noether nació en el seno de esa familia siendo la primogénita de los cuatro hermanos. Su primer nombre era Amalie, por su madre y abuela materna, pero comenzó a usar su segundo nombre cuando era joven. Emmy era miope y hablaba con un leve sigmatismo (llamado coloquialmente "ceceo") durante la infancia. Un amigo de la familia contó años más tarde una anécdota sobre la joven Emmy, quien resolvió con rapidez un acertijo en una fiesta infantil, dejando ya traslucir su capacidad para la lógica a temprana edad. A Emmy le enseñaron a cocinar y limpiar - como era costumbre en su época - y recibió lecciones de piano. No se apasionó mucho por ninguna estas actividades, aunque le gustaba bailar.

De sus tres hermanos solo a Fritz Noether, nacido en 1884, se le recuerda por sus logros académicos. Tras estudiar en Múnich se creó una reputación en el campo de la matemática aplicada. Su hermano mayor, Alfred, quien nació en 1883, obtuvo un doctorado en química por la Universidad de Erlangen-Núremberg en 1909, pero murió nueve años después. El menor de sus hermanos, Gustav Robert, nació en 1889. Se sabe muy poco sobre su vida. Sufría una enfermedad crónica y falleció en 1928.

Estudios y trayectoria profesional

Emmy Noether no mostró de niña una capacidad especial para las matemáticas, interesándose más por la música y el baile. Estudió el bachillerato en un colegio para chicas donde las matemáticas no tenían gran peso. En abril de 1900 aprobó los exámenes estatales de francés e inglés con calificación de sehr gut (sobresaliente), lo cual la capacitaba para enseñar idiomas en escuelas femeninas. Pero en 1903 se permitió por primera vez que las mujeres estudiaran en las universidades de Baviera; dos años antes, el senado académico de la universidad había declarado que la coeducación podría "subvertir todo el orden académico". Emmy optó por acudir al Realgymnasium de Nuremberg para obtener allí, como alumna libre, el Abitur (título de bachillerato que da acceso a la universidad). Durante el semestre de invierno 1903-04 estudió en la Universidad de Gotinga, asistiendo como oyente a clases impartidas por el astrónomo Karl Schwarzschild y los matemáticos Hermann Minkowski, Otto Blumenthal, Felix Klein y David Hilbert. Posteriormente pudo matricularse en la Universidad de Erlangen, donde impartía clases su padre. En 1907, bajo la supervisión de Paul Gordan, escribió su tesis Über die Bildung des Formensystems der ternären biquadratischen Form (Sobre la construcción del sistema formal de la forma ternaria bicuadrática). Aunque fue bien acogida, Noether describió posteriormente su tesis como bazofia. Se había convertido en la segunda mujer alemana que obtenía el doctorado en matemáticas en una universidad alemana. En 1908 se asoció al Circolo Matematico di Palermo y al año siguiente se afilió a la Deutschen Mathematiker-Vereinigung (Asociación alemana de matemáticos).

Durante los años 1908-1915 impartió clases en el Instituto matemático de la Universidad de Erlangen sin percibir emolumentos, sustituyendo ocasionalmente a su padre cuando se encontraba demasiado postrado para dar clase. En 1910 y 1911 publicó una ampliación de su tesis doctoral generalizando el caso de 3 variables a n variables.

El Kollegienhaus de Erlangen, uno de los edificios de la antigua universidad donde se graduó y dio sus primeras lecciones Emmy Noether.

En la Universidad de Gotinga

En la primavera de 1915, Noether fue invitada a regresar a la Universidad de Gotinga, que en ese momento era un centro de investigación matemática de fama mundial por David Hilbert y Felix Klein. No obstante, sus esfuerzos por reclutarla fueron bloqueados por los filólogos e historiadores de la Facultad de Filosofía, con el argumento, según ellos, de que las mujeres no debían acceder a la condición de privatdozent (profesor asociado). Uno de los miembros de la facultad protestó diciendo "¿qué pensarán nuestros soldados cuando vuelvan a la universidad y encuentren que se les pide que aprendan poniéndose a los pies de una mujer?" Hilbert respondió con indignación, espetando: "No veo por qué el sexo de un candidato pueda ser un argumento en contra de su admisión como privatdozent. Después de todo, somos una universidad, no un establecimiento de baños."

Noether se fue a Gotinga a finales de abril. Dos semanas más tarde su madre murió de repente. Previamente había recibido un tratamiento por una afección ocular, pero se desconoce su naturaleza y el impacto que sobre ella tuvo la desaparición de su madre. Por esas fechas el padre de Emmy se jubiló y su hermano se alistó en el ejército de Alemania para combatir en la Primera Guerra Mundial. Regresó a Erlangen durante algunas semanas, principalmente para ocuparse de su anciano padre.

Durante los primeros años como profesora en Gotinga no tuvo una plaza oficial ni percibía retribución. Su familia le pagaba el alojamiento y manutención, sufragando de ese modo su labor académica. Frecuentemente sus clases se anunciaban con el nombre de Hilbert y tenía la consideración de "ayudante".

No obstante, poco después de llegar a Gotinga mostró su capacidad probando el teorema que hoy en día lleva su nombre, que muestra que toda ley de conservación en un sistema físico proviene de alguna simetría diferenciable del mismo. El físico estadounidense Leon M. Lederman y Christopher T. Hill argumentan en su libro Symmetry and the Beautiful Universe que el teorema de Noether es "ciertamente uno de los más importantes teoremas matemáticos jamás probados que guiaron el desarrollo de la física moderna, posiblemente al mismo nivel que el teorema de Pitágoras".

El departamento de matemáticas de la Universidad de Gotinga permitió la habilitación de Noether en 1919, cuatro años después de que hubiera comenzado a dar clases en su facultad.

Cuando finalizó la primera guerra mundial, la Revolución de Noviembre trajo un cambio significativo en los usos sociales, lo que se tradujo en más derechos para las mujeres. En 1919 la Universidad de Gotinga permitió a Noether optar a su habilitación (capacidad de ejercer como profesora). El examen oral tuvo lugar a finales de mayo, y la lección de habilitación la pronunció con éxito en junio.

Tres años después recibió una carta del Ministerio prusiano de Ciencia, Arte y Educación Pública en el que se le confería el título de nicht beamteter ausserordentlicher Professorin (Profesora no funcionaria extraordinaria, es decir, con derechos y funciones administrativas limitadas).). Este cargo era un profesorado "extraordinario" sin paga, no correspondiente al profesorado titular u ordinario, que conllevaba la condición de funcionario público. Aunque se reconocía la importancia de su trabajo, el puesto aún no implicaba la percepción de un salario. Noether no fue retribuida por sus clases hasta que fue designada para su puesto especial de Lehrauftrag für Algebra (catedrática de álgebra) un año después.

Continuó siendo uno de los miembros más importantes del departamento de matemáticas de Gotinga hasta 1933; sus alumnos a veces eran conocidos como "los chicos de Noether". En 1924 el matemático holandés B. L. van der Waerden se unió a su círculo y pronto comenzó a ser el principal expositor de las ideas de Noether: su trabajo fue el fundamento del segundo volumen de su influyente libro de texto, publicado en 1931, Moderne Algebra. Cuando pronunció su alocución en la sesión plenaria de 1932 del Congreso Internacional de Matemáticos en Zúrich, su acervo algebraico ya era mundialmente reconocido. En los siguientes años, el gobierno nazi de Alemania expulsó a los judíos que ocupaban puestos en las universidades, y Noether tuvo que emigrar a Estados Unidos para ocupar una plaza en el Bryn Mawr College de Pensilvania. En 1935 sufrió una operación de quiste ovárico y, a pesar de los signos de recuperación, falleció cuatro días después, a la edad de 53 años.

El trabajo de Noether en matemáticas se divide en tres épocas: En la primera (1908-1919), efectuó contribuciones significativas a la teoría de los invariantes y de los cuerpos numéricos. Su trabajo sobre los invariantes diferenciales en el cálculo de variaciones, el llamado teorema de Noether ha sido calificado "uno de los teoremas matemáticos más importantes jamás probados de entre los que guían el desarrollo de la física moderna". En su segunda época (1920-1926), comenzó trabajos que "cambiaron la faz del álgebra [abstracta]". En su artículo clásico Idealtheorie in Ringbereichen (La teoría de ideales en los anillos, 1921) Noether transformó la teoría de ideales en los anillos conmutativos en una poderosa herramienta matemática con aplicaciones muy variadas. Efectuó un uso elegante de la condición de la cadena ascendente, y los objetos que la satisfacen se denominan noetherianos en su honor. En la tercera época (1927-1935), publicó sus principales obras sobre álgebras no conmutativas y números hipercomplejos y unió la teoría de la representación de los grupos con la teoría de módulos e ideales.

Además de sus propias publicaciones, Noether fue generosa con sus ideas y se le atribuye el origen de varias líneas de investigación publicadas por otros matemáticos, incluso en campos muy distantes de su trabajo principal, como la topología algebraica.

Trabajos determinantes para el álgebra abstracta

Aunque el teorema de Noether tiene un profundo efecto sobre la física, entre los matemáticos es célebre por ser uno de los que iniciaron el campo del álgebra abstracta. Como dice Nathan Jacobson en su introducción a los Collected Papers (Artículos reunidos) de Noether:

El desarrollo del álgebra abstracta, que es una de las más importantes innovaciones de las matemáticas del siglo XX, se debe en gran medida a ella - por sus publicaciones, clases e influencia personal sobre sus contemporáneos.

La obra fundamental para el álgebra de Noether comenzó en 1920. Cuando pudo contar con la colaboración de W. Schmeidler publicó un artículo sobre la teoría de ideales en la que definía los ideales por la izquierda y por la derecha en un anillo. Los años siguientes publicó un artículo que se convirtió en un hito, titulado Idealtheorie in Ringbereichen, analizando la condición de la cadena ascendente al respecto de los ideales. Un notable algebrista, Irving Kaplansky, calificó su trabajo de "revolucionario", y su publicación dio lugar al término anillo noetheriano. También otros objetos matemáticos fueron renombrados como "noetherianos".

En 1924, un joven matemático holandés, B. L. van der Waerden, llegó a la Universidad de Gotinga. Inmediatamente comenzó a trabajar con Noether, quien le proporcionó métodos de incalculable valor en la conceptualización abstracta. Van der Waerden dijo posteriormente que su originalidad estaba "absolutamente más allá de cualquier comparación". En 1931 publicó Moderne Algebra, un texto central para este campo. Su segundo volumen está enormemente influenciado por el trabajo de Noether. Aunque Emmy no buscaba el reconocimiento, Bartel incluyó como nota en su séptima edición la observación "basado en parte en las clases de E. Artin y E. Noether". En ocasiones permitió que sus colegas y alumnos recibieran la atribución de sus ideas, ayudándoles a desarrollar sus carreras a expensas de ella misma.

Las visitas de Van der Waerden eran parte de una convergencia de los matemáticos de todo el mundo hacia Gotinga, que se convirtió en el centro más importante de contacto entre la investigación en física y matemáticas. De 1926 a 1930 el topólogo ruso Pavel Alexandrov dio una clase en la universidad. Noether y él rápidamente se convirtieron en buenos amigos. Comenzó a referirse a ella como der Noether (el Noether), utilizando el artículo nominativo masculino singular alemán como apelativo cariñoso para mostrar su respeto hacia ella. Ella intentó buscar la manera de obtener un puesto para él en Gotinga como profesor regular, pero solo fue capaz de ayudarle a asegurarse una beca de la Fundación Rockefeller. Ambos se encontraban con regularidad y disfrutaban discutiendo sobre los puntos en común del álgebra y la topología. En su alocución en el homenaje que recibió en 1935, Alexandrov se refirió a Emmy Noether como "el más grande matemático de todos los tiempos".

Docencia y alumnado

En Gotinga, Noether supervisó más de una docena de doctorados. El primero fue Grete Hermann, quien defendió su tesis en febrero de 1925. Posteriormente habló reverentemente de su "madrina de tesis". Noether también dirigió la tesis de Max Deuring, quien se distinguió como estudiante de grado y continuó contribuyendo significativamente en el campo del álgebra aritmética. Hans Fitting, a quien se conoce por el teorema de Fitting y el lema de Fitting. Zeng Jiongzhi, quien probó el teorema de Tsen. También trabajó estrechamente con Wolfgang Krull, quien hizo avanzar grandemente el álgebra conmutativa con su Hauptidealsatz (teorema del ideal principal) y su teoría de la dimensión en el álgebra conmutativa, para anillos conmutativos.

Además de su instinto para las matemáticas, Noether fue respetada por su consideración hacia los demás. Aunque algunas veces se comportó duramente contra los que le contradecían, se ganó reputación por su solicitud y paciencia con los alumnos nuevos. Su lealtad a la precisión matemática hizo que un colega la calificara como una "crítica severa", pero combinó su exigencia de precisión con una actitud casi maternal. Un colega posteriormente la describió de este modo: "completamente desprendida de cualquier egoísmo y libre de vanidad, jamás pidió nada para sí, sino que promovió el trabajo de sus alumnos por encima de todo".

Su estilo de vida frugal se debía a que se le negaron los emolumentos por su trabajo. No obstante, a pesar de que la universidad comenzó a retribuirle con un pequeño salario en 1923, continuó viviendo de forma modesta. Se le retribuyó de forma más generosa al final de su vida, pero ahorraba la mitad de su salario para ayudar a su sobrino, Gottfried E. Noether.

Mayormente despreocupada por su aspecto y modales, se centró exclusivamente en sus estudios hasta el punto de excluir la posibilidad de una relación romántica o de seguir la moda. Una importante algebrista, Olga Taussky-Todd, describió un refrigerio para mujeres, en el que Noether, totalmente metida en una discusión matemática, "escupía su comida constantemente y se limpiaba en su vestido, sin que esto le afectase lo más mínimo". Los alumnos más preocupados por las apariencias no soportaban que usase la blusa de moquero y se desentendiese de su pelo, cada vez más revuelto a medida que avanzaba la clase. Dos alumnas se acercaron a ella en una ocasión en el descanso de una clase de dos horas para expresar sus preocupaciones, pero fueron incapaces de meter baza en la enérgica discusión matemática que estaba manteniendo con otros alumnos en ese momento.

De acuerdo con el obituario pronunciado por van der Waerden tras la muerte de Emmy Noether, ella no seguía un programa preestablecido en sus clases, lo cual frustraba a algunos alumnos. Sus clases eran un tiempo de discusión espontánea con sus alumnos, para pensar y clarificar los problemas más avanzados del momento en matemáticas. Algunos de los resultados más importantes se desarrollaron en estas clases, y los apuntes de los estudiantes acabaron formando la base de varios textos importantes, como los de van der Waerden y Deuring.

Varios de sus colegas asistían a sus clases, y ella permitía que algunas de sus ideas, como la del "producto cruzado" (verschränktes Produkt en alemán) de álgebras asociativas fueran publicadas por otros. Existe un registro en el que figura Noether como profesora de cursos que duraron al menos cinco semestres en Gotinga:

• Invierno de 1924/25: Gruppentheorie und hyperkomplexe Zahlen (Teoría de grupo y números hipercomplejos)
• Invierno de 1927/28: Hyperkomplexe Grössen und Darstellungstheorie (Cantidades hipercomplejas y teoría de la representación)
• Verano de 1928: Nichtkommutative Algebra (Álgebra no conmutativa)
• Verano de 1929: Nichtkommutative Arithmetik (Aritmética no conmutativa)
• Invierno de 1929/30: Algebra der hyperkomplexen Grössen (Álgebra de cantidades hipercomplejas)

Estos cursos con frecuencia precedían a publicaciones importantes en estas áreas. Noether hablaba muy rápido —reflejando la rapidez de sus pensamientos, según decían muchos— y pedía gran concentración a sus alumnos. Aquellos a los que les desagradaba su estilo, se sentían a menudo alienados. Uno de ellos escribió en un cuaderno con respecto a una clase que terminó a la 1:00 p. m.: "Son las 12:50, ¡gracias a Dios!" Algunos alumnos pensaban que se basaba demasiado en discusiones espontáneas. Sin embargo, sus alumnos más aplicados se solazaban en el entusiasmo con que transmitía las matemáticas, especialmente porque sus clases con frecuencia se hacían sobre los trabajos más recientes que habían elaborado juntos.

Desarrolló un círculo cerrado de colegas y estudiantes que pensaban de forma similar y tendían a excluir a quienes no lo hacían así. Los "outsiders" que ocasionalmente visitaban las clases de Noether solían pasar solo 30 minutos en el aula antes de abandonarla envueltos en la frustración o la confusión. Uno de sus estudiantes habituales anotó así uno de estos incidentes: "El enemigo ha sido derrotado; se ha ido."

La devoción de Noether por su profesión y sus alumnos no entendía de horas lectivas. Una vez que el edificio de la universidad estaba cerrado por vacaciones, reunió a su clase en las escaleras de la entrada, la llevó por el bosque y les dio clase en una cafetería local. Más tarde, al ser relegada por el Tercer Reich, habría de invitar a sus alumnos a su casa para discutir sus futuros planes y conceptos matemáticos.

En Moscú

Noether enseñó en la Universidad Estatal de Moscú en el invierno de 1928-29.

En el invierno de 1928-29 Noether aceptó una invitación de la Universidad Estatal de Moscú, donde continuó trabajando con P. S. Alexandrov. Además de continuar con sus investigaciones, impartió clases de álgebra abstracta y geometría algebraica. Trabajó con los topólogos Lev Pontryagin y Nikolai Chebotaryov, quienes más tarde agradecieron su contribución al desarrollo de la teoría de Galois.

Aunque la política no fue central en su vida, Noether se tomó cierto interés en asuntos políticos, y según Alexandrov, mostró un considerable apoyo a la revolución rusa de 1917. Emmy se sentía especialmente feliz por ver los avances soviéticos en los campos de la ciencia y las matemáticas, que consideraba indicativos de las nuevas oportunidades que brindaba el proyecto bolchevique. Esta actitud le trajo problemas en Alemania, culminando en el desalojo de la pensión donde vivía a causa de las protestas de los cabecillas estudiantiles que se quejaban por vivir con una "judía marxista".-

Noether planeó volver a Moscú, un empeño en el que recibió el apoyo de Alexandrov. Después de que dejara Alemania en 1933, intentó obtener una cátedra en la Universidad Estatal de Moscú a través del Narkompros. Aunque su esfuerzo no tuvo éxito, mantuvo correspondencia frecuente durante los años 1930 y en 1935 hizo planes para volver a la Unión Soviética. Mientras tanto su hermano Fritz había aceptado un puesto en el Instituto para la Investigación en Matemáticas y Mecánica de Tomsk, Rusia, tras perder su empleo en Alemania.

Reconocimiento

En 1932 Emmy Noether y Emil Artin recibieron el Premio Ackermann-Teubner Memorial por su contribución a las matemáticas. El premio conllevaba una recompensa en metálico de 500 Reichsmarks y fue visto como un reconocimiento oficial largo tiempo demorado por sus considerables trabajos en el campo. No obstante, sus colegas expresaron frustración por el hecho de que no fuera elegida para la Academia de Ciencias de Gotinga y jamás fue promovida al puesto de Ordentlicher Professor (catedrática).

Noether visitó Zúrich en 1932 para dirigirse al plenario del Congreso Internacional de Matemáticos.

Los colegas de Noether celebraron su cincuenta cumpleaños en 1932 al modo típico de los matemáticos: Helmut Hasse le dedicó un artículo en los Mathematische Annalen, donde confirmó su sospecha de que algunos aspectos de la álgebra no conmutativa son más simples que los de la conmutativa probando una ley de reciprocidad no conmutativa. Esto complació inmensamente a Noether. Hasse también le envió un acertijo matemático, el "acertijo de sílabas mμν", que resolvió inmediatamente. El acertijo se ha perdido.

En septiembre del mismo año Noether pronunció una alocución (großer Vortrag) al plenario del Congreso Internacional de Matemáticos de Zúrich sobre los "Sistemas hipercomplejos en sus relaciones con el álgebra conmutativa y la teoría de números". Al congreso asistieron ochocientas personas, entre ellas los colegas de Noether Hermann Weyl, Edmund Landau y Wolfgang Krull. Había cuatrocientos veinte participantes oficiales y se presentaron veintiuna alocuciones al plenario. Aparentemente, la posición prominente de Noether como conferenciante era un reconocimiento de la importancia de su contribución a la matemática. El congreso de 1932 se describe en ocasiones como el punto álgido de su carrera.

Expulsión de Gotinga

Cuando Adolf Hitler se convirtió en Reichskanzler en enero de 1933, el activismo nazi en el país se incrementó dramáticamente. En la Universidad de Gotinga la Asociación de Estudiantes de Alemania llevó a cabo un ataque contra lo que para ellos suponía el "espíritu antialemán" y en ello fueron auxiliados por un privatdozent llamado Werner Weber, antiguo alumno de Emmy Noether. Las actitudes antisemitas crearon un clima hostil para los profesores judíos. Se recuerda la historia de un joven manifestante que entre sus demandas hablaba de que "los estudiantes arios querían matemáticos arios y no matemáticos judíos."

Una de las primeras acciones del gobierno de Hitler fue la Ley para la Restauración del Servicio Civil Profesional que cesó de su puesto a los funcionarios judíos y políticamente sospechosos — a menos de que hubieran demostrado su lealtad a Alemania sirviendo en la primera guerra mundial. En abril de 1933 Noether recibió una notificación del Ministerio Prusiano de Ciencias, Arte y Educación pública que le comunicaba que "En base al párrafo 3 del Código del Servicio Civil del 7 de abril de 1933, por la presente le retiro el derecho de enseñar en la Universidad de Gotinga." A algunos de los colegas de Noether, incluyendo Max Born y Richard Courant, también les fueron revocados sus puestos. Noether aceptó la decisión con calma, apoyando a otros durante aquellos difíciles momentos. Hermann Weyl escribió posteriormente que "Emmy Noether —su valor, franqueza, su despreocupación por su propio destino, su espíritu conciliador, a pesar de la desolación que nos rodeaba, era un alivio moral." Como era de esperar, Noether continuó concentrada en las matemáticas, reuniendo a los alumnos en su apartamento para discutir sobre la teoría de los cuerpos de clases. Cuando uno de sus estudiantes apareció vestido con el uniforme de la organización paramilitar nazi Sturmabteilung (SA), no mostró ningún signo de preocupación y, según se dijo, incluso le sonrió más tarde.

Bryn Mawr

El Bryn Mawr College dio un hogar acogedor a Noether durante los dos últimos años de su vida.

Como docenas de profesores que se habían quedado sin empleo comenzaron a buscar puestos docentes fuera de Alemania, sus colegas de los Estados Unidos le buscaron asistencia y oportunidades laborales. Albert Einstein y Hermann Weyl fueron elegidos por el Instituto de Estudios Avanzados de Princeton mientras que otros trabajaron para encontrar el patrocinador que se precisaba en los trámites de inmigración. Noether fue contactada por representantes de dos instituciones educativas, el Bryn Mawr College en Estados Unidos y el Somerville College en la Universidad de Oxford, Inglaterra. Tras una serie de negociaciones con la fundación Rockefeller, se aprobó la concesión de una beca para Noether en Bryn Mawr y obtuvo un puesto allí, comenzando a finales de 1933.

En Bryn Mawr, Noether conoció y trabó amistad con Anna Wheeler, quien había estudiado en Gotinga justo antes de que Noether llegara allí. Otra fuente de apoyo en el College fue la presidenta de Bryn Mawr, Marion Edwards Park, quien invitó con entusiasmo a los matemáticos locales para que vieran a la "doctora Noether en acción". Noether y un pequeño grupo de estudiantes trabajaron rápidamente con el libro de 1930 de van der Waerden Álgebra Moderna I y partes de la Theorie der algebraischen Zahlen de Erich Hecke (Teoría de números algebraicos, 1908).

En 1934, Noether comenzó a dar clases en el Instituto de Estudios Avanzados de Princeton por invitación de Abraham Flexner y Oswald Veblen. También trabajó y supervisó a Abraham Albert y Harry Vandiver. No obstante, sobre la Universidad de Princeton (vinculada, pero distinta del Instituto de Estudios Avanzados de Princeton) observó que no fue bien recibida en "una universidad de hombres, donde no se admitía a ninguna mujer". Sus días en los Estados Unidos fueron placenteros, rodeada como estaba de colegas que le apoyaban y absorbían con sus temas favoritos. En el verano de 1934 retornó por un corto tiempo a Alemania para encontrarse con Emil Artin y su hermano Fritz antes de dirigirse a Tomsk. Aunque muchos de sus anteriores colegas habían sido obligados a abandonar la universidad, pudo usar la biblioteca como "investigadora invitada extranjera".

Fallecimiento

Los restos mortales de Emmy Noether se encuentran en el pasaje que rodea el claustro de la Biblioteca M. Carey Thomas.

En abril de 1935 los médicos le descubrieron un tumor pélvico. Preocupados por las posibles complicaciones de la cirugía, le ordenaron dos días de reposo en cama antes de proceder a la intervención. Durante la misma descubrieron un quiste ovárico "del tamaño de un melón". Dos tumores uterinos más pequeños parecían ser benignos y no fueron extirpados para evitar que se prolongara la operación. Durante tres días parecía que la convalecencia seguía un curso normal, y se recobró rápidamente de un colapso circulatorio que se produjo el cuarto día. El 14 de abril perdió la consciencia, su temperatura se elevó a 42,5 °C y finalmente falleció. "No es fácil decir qué le sucedió a la Doctora Noether", escribió uno de los facultativos, "es posible que hubiera algún tipo inusual y violento de infección que afectó a la base del cerebro, que es donde se supone que se localizan los centros termorreguladores."

Unos días después de la muerte de Noether, sus amigos y allegados en Bryan Mawr celebraron un servicio en su memoria en la President Park's house. Hermann Weyl y Richard Brauer viajaron desde Princeton y hablaron con Wheeler y Taussky sobre su colega desaparecida. En los meses que siguieron, comenzaron a aparecer homenajes por escrito por todo el mundo: Al de Albert Einstein se unió el de van der Waerden, Weyl y Pavel Alexandrov para presentar sus respetos. Su cuerpo fue incinerado y las cenizas enterradas en el claustro de la biblioteca M. Carey Thomas Library en Bryn Mawr.

Contribución a la matemática y la física

En primer lugar y ante todo, Noether es recordada en las matemáticas como algebrista y por sus trabajos en la topología. Los físicos la aprecian más por el famoso teorema que lleva su nombre puesto que tiene consecuencias de gran alcance para el estudio de las partículas subatómicas y la dinámica de sistemas. Mostró una aguda propensión para el pensamiento abstracto, lo que le permitía acercarse a problemas matemáticos de una forma original. Su amigo y colega Hermann Weyl describió su trabajo como autoridad en tres épocas claramente distintas:

(1) Periodo de relativa dependencia, 1907-1919;

(2) Las investigaciones agrupadas en torno a la teoría general de ideales 1920-1926;

(3) El estudio de álgebras no conmutativas, sus representaciones mediante transformaciones lineales y sus aplicaciones al estudio de los cuerpos no conmutativos y sus aritméticas. (Weyl, 1935)

En la primera época (1908-19), Noether se ocupó en primer lugar de los invariantes diferenciales y algebraicos, comenzando con la defensa de su tesis bajo la dirección de Paul Albert Gordan. Sus horizontes matemáticos se ampliaron, y su trabajo comenzó a hacerse más general y abstracto a medida que se fue familiarizando con el trabajo de David Hilbert, gracias a estrechas interacciones con el sucesor de Gordan, Ernst Sigismund Fischer. Después de su traslado a Gotinga en 1915, elaboró el trabajo que posteriormente se mostró de capital importancia para la física, el teorema de Noether.

En la segunda época (1920-26), Noether se dedicó al desarrollo de la teoría de anillos.

En su tercera época (1927-35), Noether se centró en el álgebra no conmutativa, transformaciones lineales y cuerpos conmutativos numéricos.

Contexto histórico

En el siglo transcurrido desde 1832 hasta el fallecimiento de Noether en 1935, el campo de las mátemáticas —específicamente el álgebra— sufrió una profunda revolución, cuyos ecos aún se sienten. Los matemáticos de los siglos anteriores trabajaron en métodos prácticos para resolver tipos específicos de ecuaciones, por ejemplo las ecuaciones cúbicas, y de cuarto y quinto grado, así como problemas relacionados con la construcción de polígonos regulares con regla y compás. Comenzando con la prueba efectuada por Carl Friedrich Gauss en 1829 de que un número primo como cinco podía ser factorizado en enteros de Gauss, la introducción por parte de Évariste Galois del concepto de grupo en 1832, y el descubrimiento por parte de William Rowan Hamilton de los cuaterniones en 1843, las investigaciones matemáticas iban determinando las propiedades de sistemas cada vez más abstractos definidos por reglas cada vez más universales. Las contribuciones más importantes de Noether a las matemáticas vinieron por el desarrollo de este nuevo campo, el álgebra abstracta.

Álgebra abstracta y begriffliche Mathematik (matemática conceptual)

Dos de los dos objetos más básicos en el álgebra abstracta son los grupos y los anillos.

Un grupo consiste en un conjunto dotado de una operación que combina dos elementos cualesquiera y da un tercero. La operación debe satisfacer ciertas condiciones para ser un grupo: debe ser cerrada (cuando se aplica a cualquier par de elementos, el elemento generado debe pertenecer también al conjunto), debe ser asociativa, debe tener un elemento neutro (un elemento que combinado mediante la operación con cualquier otro da como resultado el elemento original, como sumar cero o multiplicar por uno), y para cada elemento debe existir un elemento inverso.

Un anillo es un conjunto dotado de dos operaciones. La primera da al conjunto estructura de grupo, y la segunda operación es asociativa y distributiva con respecto a la primera operación. Puede o no ser conmutativa. Si cada elemento distinto de cero tiene un inverso multiplicativo (un elemento x tal que ax = xa = 1), el anillo se llama anillo de división. Un cuerpo se define como un anillo de división conmutativo.

Los grupos se estudian frecuentemente mediante representaciones de grupo. En su forma más general, estas consisten en tomar un valor del grupo, un conjunto, y una acción del grupo sobre el conjunto, esto es, una operación externa que toma un elemento del grupo y un elemento del conjunto, y da un elemento del conjunto. Con frecuencia, el conjunto es un espacio vectorial y el grupo está representado por simetrías del espacio vectorial. Por ejemplo, hay grupos que pueden representarse mediante rotaciones del espacio. Noether consideró este tipo de simetrías en su trabajo sobre los invariantes en física.

Una forma poderosa de estudiar los anillos es a través de sus módulos. Un módulo consiste en un valor de un anillo, otro conjunto, normalmente distinto del conjunto subyacente llamado el conjunto subyacente del módulo, una operación sobre pares de elementos del conjunto subyacente del módulo y una operación que toma un elemento del anillo y un elemento del módulo y da un elemento del módulo. El conjunto subyacente del módulo y su operación deben formar un grupo. Un módulo es una versión de la teoría de anillos de una representación de grupo: ignorando la segunda operación del anillo y la operación sobre pares de elementos del módulo determina una representación de grupo. La utilidad real de los módulos es que los tipos de módulos que existen y sus interacciones se revela la estructura del anillo de formas que no son evidentes a partir del propio anillo. Un caso especial importante de esto es un álgebra. La palabra álgebra significa tanto un tema dentro de las matemáticas como un objeto más específico estudiado dentro de la propia álgebra. En esta segunda acepción consiste en una elección de dos anillos y una operación que toma un elemento de cada anillo y da un elemento del segundo anillo. Esta operación la efectúa el segundo anillo en un módulo sobre el primero. Con frecuencia el primer anillo es un cuerpo.

Palabras como "elemento" y "operación de combinación" son demasiado generales y se pueden aplicar a muchas situaciones abstractas y del mundo real. Cualquier conjunto de cosas que obedezcan las reglas de una (o dos) operaciones es, por definición, un grupo (o anillo), y obedece a todos los teoremas sobre grupos (o anillos). Los números eneteros y las operaciones de adición y multiplicación son solo un ejemplo. Por ejemplo, los elementos pueden ser datos de computación en palabras, en la que la primera operación de combinación es la disyunción exclusiva y la segunda es una conjunción lógica. Los teoremas del álgebra abstracta son potentes porque son generales. Gobiernan muchos sistemas. Se puede imaginar que poco se puede concluir sobre objetos definidos con tan pocas propiedades, pero precisamente en esto radica el legado de Noether: descubrir lo máximo que se pueda concluir a partir de un conjunto dado de propiedades, o dicho de otro modo, identificar el mínimo de las propiedades esenciales de una observación en particular. A diferencia de la mayor parte de los matemáticos, no realizó abstracciones generalizando a partir de ejemplos conocidos. En lugar de ello trabajó directamente con las abstracciones. Como recordó van der Waerden en el obituario de Emmy:

La máxima por la que se guiaba Emmy Noether a lo largo de su obra podría ser formulada como sigue: «Cualquier relación entre números, funciones y operaciones se hace transparente, generalmente aplicable y completamente productiva solo si ha sido aislada a partir de objetos particulares y formulada como conceptos universalmente válidos».

Esto es la llamada begriffliche Mathematik (matemática conceptual) que es característica de Noether. Este estilo de matemáticas fue adoptado por otros matemáticos, y tras su muerte floreció en nuevas formas como la teoría de categorías.

Enteros como ejemplo de un anillo

Los enteros forman un anillo conmutativo cuyos elementos son los enteros, y las operaciones de combinación son la adición y la multiplicación. Cualquier par de enteros pueden ser sumados o multiplicados, lo cual resulta siempre en otro entero, y la primera operación, la adición, es conmutativa, p. ej. para cualquier elemento a y b del anillo, a + b = b + a. La segunda operación, la multiplicación, también es conmutativa, pero eso no necesita ser cierto para otros anillos, lo que significa que a combinada con b puede ser diferente de b combinada con a. Ejemplos de anillos no conmutativos serían las matrices y los cuaterniones. Los enteros no forman un anillo de división, porque la segunda operación no siempre puede ser invertida: no existe un entero a tal que 3 × a = 1.

Los enteros tienen propiedades adicionales que no se generalizan a todos los anillos conmutativos. Un ejemplo importante es el teorema fundamental de la aritmética, que dice que cada entero positivo puede ser factorizado únicamente en números primos. Las factorizaciones únicas no siempre existen en otros anillos, pero Noether encontró un único teorema de factorización, conocido actualmente como el teorema de Lasker-Noether theorem, para ideales de muchos anillos. Gran parte del trabajo de Noether se centra en determinar qué propiedades corresponden a todos los anillos, en diseñar nuevos análogos de los viejos teoremas sobre los enteros y en determinar el mínimo conjunto de premisas necesarias para obtener ciertas propiedades de los anillos.

Primera época (1908-19)

Teoría de la invariante algebraica

Tabla 2 de la tesis doctoral de Noether sobre la teoría de los invariantes. Esta tabla recoge 202 de las 303 invariantes en formas ternarias bicuadráticas. Estas formas se gradúan en dos variables x y u. La dirección horizontal de la tabla lista los invariantes con grado progresivamente mayor en x, mientras la dirección vertical lista las mismas con grados progresivamente mayores en u.

Gran parte del trabajo de Noether en la primera época de su carrera estaba asociado con la teoría de los invariantes, principalmente la teoría de las invariantes algebraicas. La teoría de los invariantes trata de las expresiones que permanecen constantes (invariantes) bajo grupos de transformaciones. Como ejemplo cotidiano, si una vara de medir rígida se somete a rotación, las coordenadas (x, y, z) de sus extremos cambian, pero su longitud L dada por la fórmula L² = Δx² + Δy² + Δz² permanece constante. La teoría de invariantes fue un área de investigación activa a finales del siglo XIX, promovida en parte por el programa de Erlangen de Felix Klein, de acuerdo con el cual los distintos tipos de geometría deberían ser caracterizadas por sus invariantes bajo transformaciones, por ejemplo, la razón anarmónica de la geometría proyectiva. El ejemplo arquetípico de una invariante es el discriminante B² − 4AC de una forma binaria cuadrática de Ax² + Bxy + Cy². A esta se le llama invariante porque no cambia por substituciones lineales x→ax + by, y→cx + dy con determinante ad − bc = 1. Estas substituciones forman el grupo lineal especial SL₂. (No hay invariantes bajo el grupo lineal general de todas las transformaciones lineales invertibles porque estas transformaciones pueden ser multiplicación por un factor escalar. Para remediarlo, la teoría clásica de los invariantes también considera invariantes relativas, que eran formas de invariancia salvo un factor escalar). Puede preguntarse por todos los polinomios en A, B, and C que no cambien por la acción de SL₂; a estos se les llama invariantes de las formas cuadráticas, y resultan ser los polinomios del discriminante. De modo más general, se puede preguntar por los invariantes de los polinomios homogéneos A₀x^ry⁰ + ... + A_rx⁰y^r de grado superior, que serán ciertos polinomios en los coeficientes A₀, ... , A_r, y de forma aún más general, se pueden plantear cuestiones similares sobre las polinomios homogéneos en más de dos variables.

Una de las principales metas de la teoría de los invariantes es resolver el "problema de base finita". La suma o producto de dos invariantes cualesquiera es un invariante, y el problema de la base finita planteaba si era posible obtener todos los invariantes comenzando por una lista finita de invariantes, llamados generadores, y después añadir o multiplicar los generadores entre sí. Por ejemplo, el discriminante ofrece una base finita (con un elemento) para los invariantes de las formas binarias cuadráticas. El director de tesis de Noether, Paul Albert Gordan, fue conocido como el "rey de la teoría de los invariantes", y su principal contribución a las matemáticas fue su solución en 1870 del problema de la base finita para invariantes de polinomios homogéneos en dos variables. Probó la existencia de una base finita mediante un método constructivo para encontrar todos los invariantes y sus generadores, pero no fue capaz de desarrollar este enfoque constructivo para invariantes de polinomios en tres o más variables. En 1890 David Hilbert probó un planteamiento similar para los invariantes de polinomios homogéneos en cualquier número de variables. Es más, este método funcionaba no solo para el grupo especial lineal, sino también para alguno de sus subgrupos como el grupo especial ortogonal. Su primera prueba produjo cierta controversia porque no proporcionaba un método para construir los generadores, aunque en trabajos posteriores hizo que su método fuera constructivo. Para su tesis Noether amplió la prueba computacional de Gordan a polinomios homogéneos en tres variables. La aproximación constructiva de Noether hizo posible estudiar las relaciones entre los invariantes. Posteriormente, tras volverse hacia métodos más abstractos, dijo de su tesis que era Mist (bazofia) y Formelngestrüpp (un revoltijo de ecuaciones).

Teoría de Galois

La teoría de Galois trata de las transformaciones de cuerpos numéricos que permutan las raíces de una ecuación. Considérese una ecuación polinómica de una variable x de grado n, en el que los coeficientes pertenecen a algún «cuerpo base», que podría ser, por ejemplo, el cuerpo de los números reales, el de los números racionales o el de los enteros módulo  7. Pueden existir o no valores de x que anulen este polinomio. Estos valores, si existen, se llaman raíces. Si el polinomio es x² + 1 y el cuerpo es el de los números reales, entonces el polinomio no tiene raíces, porque cualquier valor de x hace que el polinomio sea mayor o igual que uno. No obstante, si el cuerpo se extiende, entonces el polinomio puede tener raíces, y si se le extiende lo suficiente, tendrá un número de raíces igual a su grado. Continuando con el ejemplo previo, si el cuerpo se extiende a los números complejos, entonces el polinomio tiene dos raíces, i y −i, dondei es la unidad imaginaria, esto es, i ² = −1. De modo más general, la extensión del cuerpo en el que un polinomio puede factorizarse en sus raíces se conoce como cuerpo de descomposición del polinomio.

El grupo de Galois de un polinomio es el conjunto de todas las maneras de transformar el cuerpo de descomposición sin cambiar ni el cuerpo base ni las raíces del polinomio (en la jerga matemática, esas transformaciones se denominan automorfismos). El grupo de Galois de x² + 1 consta de dos elementos: La transformación identidad, que envía cada número complejo a sí mismo, y la conjugación, que hace corresponder i a −i. Ya que el grupo de Galois no cambia el cuerpo base, deja los coeficientes del polinomio inalterados, de modo que debe también dejar inalterado el conjunto de todas las raíces. Sin embargo, cada raíz puede transformarse en otra raíz, de modo que la transformación determina una permutación de n raíces entre sí mismas. La importancia del grupo de Galois viene del teorema fundamental de la teoría de Galois, que prueba que los cuerpos que están entre el cuerpo base y el cuerpo de descomposición están en correspondencia biunívoca con los subgrupos del grupo de Galois.

En 1918, Noether publicó un artículo de gran importancia sobre el problema inverso de Galois. En lugar de determinar el grupo de Galois de transformaciones de un cuerpo dado y su extensión, Noether se preguntó si, dado un cuerpo y un grupo, siempre es posible encontrar una extensión del cuerpo que tenga al grupo dado como su grupo de Galois. Redujo esto al llamado problema de Noether, que pregunta si el cuerpo fijo de un subrupo G del grupo de permutaciones S_n actuando sobre el cuerpo k(x₁, ... , x_n) es siempre una extensión trascendente pura del cuerpo k. (Mencionó esto por primera vez en un artículo de 1913, donde atribuía el problema a su colega Fischer.) Mostró que esto era cierto para n = 2, 3, o 4. En 1969, R. G. Swan encontró un contraejemplo para el problema de Noether siendo n = 47 y G un grupo cíclico de orden 47 (aunque este grupo puede realizarse como un grupo de Galois sobre los números racionales por otros métodos). El problema inverso de Galois continúa sin resolverse.

Física

Noether fue invitada a Gotinga en 1915 por David Hilbert y Felix Klein, quienes necesitaban de su experiencia en la teoría de invariantes para ayudarles a comprender la relatividad general, una teoría geométrica de la gravitación desarrollada principalmente por Albert Einstein. Hilbert había observado que la conservación de la energía parecía ser violada en la relatividad general, debido al hecho de que la energía gravitacional podía a su vez ejercer atracción gravitacional. Noether desmontó esta paradoja y creó una herramienta fundamental para la física teórica con su primer teorema de Noether, que demostró en 1915, pero que no publicó hasta 1918. Resolvió el problema no solo para la relatividad general, sino que determinó las cantidades conservadas para cualquier sistema de leyes físicas que posea algún tipo de simetría continua. Tras recibir su trabajo, Einstein escribió a Hilbert estas palabras: "Ayer recibí de la señorita Noether un artículo muy interesante sobre los invariantes. Me ha impresionado que este tipo de cosas puedan ser comprendidas de un modo tan general. ¡La vieja guardia de Gotinga debería tomar algunas lecciones de la señorita Noether! Parece que sabe lo que hace."

Para ilustrar la importancia de este teorema, si un sistema físico se comporta con independencia de su orientación en el espacio, se dice que las leyes físicas que lo gobiernan tienen simetría de rotación. A partir de esta simetría, el teorema de Noether muestra que el momento angular del sistema se debe conservar. El propio sistema físico no necesita ser simétrico. Un asteroide de superficie irregular que gira caóticamente en el espacio conserva su momento angular a pesar de su falta de simetría. Es la simetría de las leyes físicas que gobiernan el sistema la que es responsable de la ley de la conservación. Otros ejemplos: si un experimento físico da el mismo resultado en cualquier lugar y en cualquier momento, entonces sus leyes son simétricas bajo traslaciones (continuas) en el espacio y el tiempo. En virtud del teorema de Noether, estas simetrías explican las leyes de conservación del momento lineal y la energía de este sistema, respectivamente.

El teorema de Noether se ha convertido en una herramienta fundamental en la moderna física teórica, tanto por la perspectiva que da sobre las leyes de conservación como por ser una herramienta práctica de cálculo. El teorema permite a los investigadores determinar las cantidades conservadas a partir de las simetrías observadas en un sistema físico. Recíprocamente, facilita la descripción de un sistema físico basándose en leyes físicas hipotéticas. Para ilustrar este punto, supóngase que se descubre un nuevo fenómeno físico. Entonces los modelos teóricos que se propongan para el fenómeno deben satisfacer el teorema de Noether: si la teoría tiene una simetría continua, entonces el teorema de Noether garantiza que la teoría tiene una cantidad conservada, y para que la teoría sea correcta, esta conservación debe ser observable en experimentos.

Segunda época (1920-26)

Aunque los resultados de la primera época de Noether fueron impresionantes y útiles, su fama como matemática descansa más en el trabajo fundamental que efectuó en su segunda y tercera épocas, como advierten Hermann Weyl y B. L. van der Waerden en el obituario de Emmy.

En estas épocas no estaba aplicando meramente las ideas y métodos de los primeros matemáticos. En lugar de ello estaba elaborando nuevos sistemas de definiciones matemáticas que serían usados por futuros matemáticos. En particular, desarrolló una teoría completamente nueva de los ideales en los anillos, que generalizaba los primeros trabajos de Richard Dedekind. También es conocida por descubrir las condiciones de la cadena ascendente, una condición simple de finitud que en sus manos dio poderosos resultados. Estas condiciones y la teoría de los ideales permitieron a Noether generalizar muchos resultados antiguos y tratar viejos problemas desde nuevas perspectivas, como la teoría de la eliminación y las variedades algebraicas, que había estudiado su padre.

Condiciones ascendentes y descendentes de cadena

En esta época, Noether se hizo famosa por su destreza en el uso de las condiciones ascendentes (Teilerkettensatz) o descendentes (Vielfachenkettensatz) de cadena. Se dice que una sucesión de subconjuntos no vacíos A₁, A₂, A₃, etc. de un conjunto S es estrictamente ascendente si cada uno es un subconjunto del siguiente

La condición de cadena ascendente requiere que estas sucesiones se descompongan después de un número finito de pasos. En otras palabras, todas estas sucesiones deben ser finitas. A la inversa, con una sucesión de subconjuntos estrictamente descendente:

la condición de la cadena descendente requiere que tales sucesiones se descompongan después de un número finito.

Las condiciones ascendentes y descendentes de cadena son generales, es decir, se pueden aplicar a muchos tipos distintos de objetos matemáticos, y a primera vista no parecen muy potentes. Sin embargo Noether mostró cómo explotar esas condiciones para obtener las máximas ventajas: por ejemplo, utilizándolas para mostrar que todo conjunto de sub-objetos tiene un elemento maximal o minimal, o que un objeto complejo puede generarse a partir de un número menor de elementos. Estas conclusiones a menudo son pasos cruciales en una demostración.

Muchos tipos de objetos en un álgebra abstracta pueden satisfacer las condiciones de cadena, y habitualmente si satisfacen una condición ascendente de cadena se llaman noetherianos en su honor. Por definición, un anillo noetheriano satisface una condición ascendente de cadena en sus ideales izquierdo y derecho, mientras que un grupo noetheriano se define como un grupo en el que toda cadena estrictamente ascendente de subgrupos es finita. Un módulo noetheriano es un módulo en el que toda cadena estrictamente ascendente de submódulos se descompone después de un número finito. Un espacio noetheriano es un espacio topológico en el que toda cadena estrictamente ascendente de subespacios abiertos se descompone después de un número finito de términos. Esta definición se establece de tal manera que el espectro de un anillo noetheriano es un espacio topológico noetheriano.

La condición de la cadena frecuentemente es "heredada" por los subobjetos. Por ejemplo, todos los subespacios de un espacio noetheriano son a su vez noetherianos. Todos los subgrupos y grupos cociente de un grupo noetheriano son del mismo modo noetherianos, y mutatis mutandis, lo mismo se predica de los submódulos y cocientes de módulos de un módulo noetheriano. Todos los anillos cociente de un anillo noetheriano son noetherianos, pero eso no es necesariamente válido para sus subanillos. La condición de cadena también puede heredarse por combinaciones o extensiones de un objeto noetheriano. Por ejemplo, las sumas finitas directas anillos noetherianos son noetherianas, así como el anillo de series de potencias formales sobre un anillo noetheriano.

Otra aplicación de estas condiciones de cadena es la inducción noetheriana —también conocida como orden bien fundamentado— que es una generalización de la inducción matemática. Frecuentemente se usa para reducir proposiciones generales sobre colecciones de objetos a proposiciones sobre objetos en particular de esa colección. Supóngase que S es un conjunto parcialmente ordenado. Una forma de probar una afirmación sobre los objetos de S es suponer la existencia de un contraejemplo y deducir una contradicción, probando de ese modo la contrapuesta de la afirmación original. La premisa básica de la inducción noetheriana es que todo subconjunto no vacío de S contiene un elemento minimal. En particular, el conjunto de todos los contraejemplos contiene un elemento minimal, el contraejemplo minimal. Para probar la afirmación original, por tanto, es suficiente probar algo aparentemente mucho más débil: por cada contraejemplo existe un contraejemplo menor.

Anillos conmutativos, ideales y módulos

El artículo de Noether, Idealtheorie in Ringbereichen (Teoría de ideales en dominios de integridad, 1921), es el fundamento de la teoría general de anillos conmutativos y da una de las primeras definiciones generales de un anillo conmutativo. Antes de su artículo, muchos de los resultados en el álgebra conmutativa se restringían a ejemplos especiales de anillos conmutativos, como los anillos polinómicos sobre cuerpos o anillos de enteros algebraicos. Noether probó que en un anillo que satisface la condición de cadena ascendente sobre un ideal, todos los ideales se generan de forma finita. En 1943 el matemático francés Claude Chevalley acuñó el término, anillo noetheriano, para describir esta propiedad. Una de las consecuencias principales del artículo de Noether de 1921 es el teorema de Lasker-Noether, que amplía el teorema de Lasker sobre la descomposición primaria de ideales en anillos polinómicos a todos los anillos noetherianos. El teorema de Lasker-Noether se puede contemplar como una generalización del teorema fundamental de la aritmética que afirma que cualquier entero positivo se puede expresar como un producto de números primos y que dicha descomposición es única.

El trabajo de Noether Abstrakter Aufbau der Idealtheorie in algebraischen Zahl- und Funktionenkörpern (Estructura abstracta de la teoría de ideales en cuerpos de números algebraicos y de funciones, 1927) caracterizó los anillos en los que los ideales tienen una factorización única en ideales primos como los dominios de Dedekind: los dominios integrales que son noetherianos, 0 o 1-dimensionales, y cerrados integralmente en sus cuerpos cocientes. Este artículo también contiene lo que actualmente se conoce como los teoremas de isomorfismo, que describen algunos isomorfismos naturales y otros resultados básicos acerca de los módulos noetherianos y artinianos.

Teoría de la eliminación

En 1923-24, Noether aplicó su teoría de ideales a la teoría de la eliminación—en una formulación que se atribuye a su alumno, Kurt Hentzelt — mostrando que los teoremas fundamentales de la factorización de polinomios podían trasladarse directamente. Tradicionalmente, la teoría de la eliminación se ocupa de la eliminación de una o más variables de un sistema de ecuaciones polinómicas, habitualmente mediante el método de las resultantes. Para ilustrar este punto, un sistema de ecuaciones frecuentemente puede escribirse como el producto de una matriz M (cuyos elementos son los coeficientes) por un vector v (cuyas componentes son las potencias sucesivas de x) que se iguala al vector cero, M•v = 0. Como consecuencia, el determinante de la matriz M debe ser igual a cero, lo que da lugar a una nueva ecuación en la que la variable x ha sido eliminada.

Teoría de los invariantes de grupos finitos

Técnicas como la solución no constructiva original de Hilbert al problema de la base finita no podían aplicarse para obtener información cuantitativa sobre los invariantes de una acción de grupo, y ni siquiera podían aplicarse a todas las acciones de grupo. En su artículo de 1915, Noether resolvió el problema de base finita para un grupo finito de transformaciones G que actúa sobre un espacio vectorial finito-dimensional sobre un cuerpo de característica cero. Su solución muestra que el anillo de las invariantes se genera por invariantes homogéneos cuyo grado es menor o igual al orden del grupo finito. A esto se le llama cota de Noether. Su artículo daba dos demostraciones de la cota de Noether, que permanecen válidas cuando la característica del cuerpo es coprima con |G|!, el factorial de orden |G| del grupo G. El número de generadores necesarios no satisface necesariamente la cota de Noether cuando la característica del cuerpo divide a |G|, pero Noether no fue capaz de determinar si la cota era correcta cuando la característica del cuerpo divide a |G|! pero no a |G|. Durante muchos años, determinar la verdad o falsedad de la cota en este caso fue un problema abierto conocido como la "laguna de Noether". Finalmente se resolvió de forma independiente por Fleischmann en 2000 y Fogarty en 2001, demostrando ambos que la cota sigue siendo válida.

En su artículo de 1926, Noether extendió el teorema de Hilbert a representaciones de un grupo finito sobre un cuerpo cualquiera. El nuevo caso que no se seguía de la obra de Hilbert era cuando la característica del cuerpo divide al orden del grupo. El resultado de Noether fue ampliado posteriormente por William Haboush a todos los grupos reductivos mediante su demostración de la conjetura de Mumford. En este artículo Noether también introduce el lema de la normalización de Noether, que muestra que un dominio A generado finitamente sobre un cuerpo K tiene un conjunto x₁, ... , x_n de elementos algebraicamente independientes tales que A es la clausura integral sobre K[x₁, ... , x_n].

Contribuciones a la topología

Una deformación continua (homotopía) de una taza de café en una dona (toro) y a la inversa.

Como dijeron Pavel Alexandrov y Hermann Weyl en sus obituarios a Emmy, las contribuciones de Noether a la topología ilustran su generosidad con las ideas y cómo sus intuiciones podían transformar campos completos de la matemática. En topología los matemáticos estudian las propiedades de los objetos que permanecen invariantes incluso bajo deformación continua, propiedades como su conexidad. Hay un conocido chiste que dice que un topólogo es alguien que no distingue un donut de una taza de café, porque pueden transformarse de manera continua (que en este ejemplo significa sin cerrar ni abrir nuevos agujeros) el uno en el otro.

A Noether se le atribuyen las ideas fundamentales que condujeron al desarrollo de la topología algebraica a partir de la primitiva topología combinatoria, en concreto la idea de grupos de homología. De acuerdo con lo que dice Alexandrov, Noether asistía a clases impartidas por Heinz Hopf y él mismo en los veranos de 1926 y 1927, donde "estaba continuamente haciendo observaciones, que frecuentemente eran profundas y sutiles", y continúa diciendo que:

Cuando ... en principio quedó satisfecha con una construcción sistemática de la topología combinatoria, observó inmediatamente que merecería la pena estudiar directamente el grupo de complejos algebraicos y ciclos de un poliedro dado y el subgrupo del grupo cíclico que consta de ciclos homólogos a cero. En lugar de la definición habitual de los números de Betti, sugirió inmediatamente definir el grupo de Betti como el cociente del grupo de todos los ciclos por el subgrupo de ciclos homólogos a cero. Esta observación ahora parece obvia. Pero en aquellos años (1925-1928) fue un punto de vista completamente nuevo.

La sugerencia de Noether de que la topología debía estudiarse algebraicamente fue adoptada inmediatamente por Hopf, Alexandrov, y otros, y se convirtió en un tema de discusión frecuente entre los matemáticos de Gotinga. Noether observó que su idea de grupo de Betti hace que la fórmula Euler-Poincaré sea fácil de comprender, y el propio trabajo de Hopf sobre esta materia "lleva la impronta de estas observaciones de Emmy Noether". Noether menciona sus propias ideas sobre la topología solo marginalmente en una publicación de 1926, donde las cita como una aplicación de la teoría de grupos.

La aproximación algebraica a la topología se desarrolló independientemente en Austria. En un curso impartido en 1926-27 en Viena, Leopold Vietoris define "grupo de homología". Walther Mayer dio una definición axiomática del mismo en 1928.

Helmut Hasse trabajó con Noether y otros para encontrar la teoría de las álgebras centrales simples.

Tercera época (1927-35)

Números hipercomplejos y teoría de la representación

Se habían llevado a cabo muchos trabajos sobre los números hipercomplejos y representaciones de grupo a principios del siglo XX, pero seguían siendo dispares. Noether unificó los resultados y dio la primera representación general de la teoría de grupos y álgebras. En resumen, Noether subsumió la teoría estructural del álgebra asociativa y de la representación de grupos en una única teoría aritmética de módulos e ideales que satisfacen las condiciones ascendentes de cadena. Este único trabajo de Noether es de fundamental importancia para el desarrollo del álgebra moderna.

Álgebra no conmutativa

Noether también fue responsable de otros avances en el campo del álgebra. Con Emil Artin, Richard Brauer, y Helmut Hasse, fundó la teoría de las álgebras centrales simples.

Un artículo muy influyente publicado por Noether, Helmut Hasse, y Richard Brauer trató de las álgebras de división, que son aquellos sistemas algebraicos en los que es posible la división. Probaron dos teoremas importantes; un teorema local-global que afirma que si un álgebra de división finita dimensional central sobre un cuerpo numérico algebraico se descompone localmente en cualquier elemento, entonces se descompone también globalmente (con lo que es trivial), y de esto dedujeron su teorema principal (Hauptsatz): todo álgebra de división central finito-dimensional sobre un cuerpo numérico algebraico F se descompone sobre una extensión cíclica ciclotómica. Estos teoremas permiten clasificar todas las álgebras de división finito dimensionales y centrales sobre un cuerpo numérico dado. Un artículo posterior mostró, como un caso especial de un teorema más general, que todos los subcuerpos maximales de un álgebra de división D son cuerpos de descomposición. Este artículo también contiene el teorema de Skolem-Noether que afirma que dos inclusiones de una extensión de un cuerpo K en un álgebra simple central finito-dimensional sobre K, son conjugados. El teorema de Brauer-Noether ofrece una caracterización de los cuerpos de descomposición de un álgebra de división central sobre un cuerpo.

Valoración, reconocimiento y homenajes

El Campus de Emmy Noether en la Universidad de Siegen es la sede del departamento de física y matemáticas. Fotografía de Bob Ionescu.

El trabajo de Noether continúa siendo relevante para el desarrollo de la física teórica y las matemáticas y nunca se la ha dejado de considerar como uno de los más grandes matemáticos del siglo XX. En su obituario, el algebrista B. L. van der Waerden dijo que su originalidad matemática estaba "absolutamente más allá de cualquier comparación", y Herman Weyl que Noether "cambió la faz del álgebra abstracta" con sus trabajos. Ya durante su vida y hasta hoy, se ha mantenido que ha sido la más grande matemática de la historia por, por ejemplo, los matemáticos Pavel Alexandrov, Hermann Weyl, y Jean Dieudonné. En una carta al The New York Times, Albert Einstein escribió:

Si se hubiera de juzgar la labor de los matemáticos vivos más competentes, la señorita Noether ha sido de lejos el genio matemático más significativo producido desde que comenzó la educación superior de las mujeres. En el reino del álgebra, en el cual los más dotados matemáticos han estado ocupados durante siglos, descubrió métodos que se han mostrado de enorme importancia para la actual generación de jóvenes matemáticos.

El 2 de enero de 1935, unos pocos meses después de su fallecimiento, el matemático Norbert Wiener escribió que:

La señorita Noether es ... la más grande matemática que jamás haya existido; y la más grande científica contemporánea de cualquier especialidad, y una autoridad como poco al mismo nivel que Madame Curie.

En la Exposición Universal de 1964 bajo el lema Matemáticas: más allá del mundo de los números, Noether fue la única mujer entre los matemáticos notables del mundo moderno.

Noether ha sido honrada en varios homenajes:

• La Association for Women in Mathematics celebra cada año sus Conferencias Noether para honrar a las mujeres matemáticas. En el folleto editado para el evento en 2005, la asociación caracteriza a Nother como "uno de los matemáticos más importantes de su tiempo, alguien que trabajó y sufrió por aquello en lo que creía y amaba. Su vida y obra serán para nosotras una gran inspiración".
• En consistencia con su dedicación a sus alumnos, la Universidad de Siegen ha reunido sus facultades de matemáticas y física en el llamado "Campus Emmy Noether".
• La Sociedad Alemana para la Investigación Científica (Deutsche Forschungsgemeinschaft) lleva a cabo el Emmy Noether Programm, una beca posdoctoral para apoyar la investigación y la docencia de jóvenes prometedores.
• Una calle de su ciudad natal, Erlangen, lleva el nombre Emmy Noether y Max Noether (su padre).
• La escuela secundaria sucesora de aquella a la que asistió en Erlangen ha sido rebautizada como the Emmy Noether School.

Y, más lejos...

• El cráter Nöther en la cara oculta de la Luna fue nombrado así en su honor.
• El asteroide (7001) Noether también debe su nombre a Emmy Noether.

Lista de doctorados

Véase también

En inglés: Emmy Noether Facts for Kids