Teoría de Galois para niños
En matemáticas, la teoría de Galois es un conjunto de ideas que conectan dos ramas importantes de las matemáticas: la teoría de cuerpos y la teoría de grupos. Gracias a esta teoría, algunos problemas difíciles sobre ecuaciones se pueden transformar en problemas más sencillos de la teoría de grupos. La teoría de Galois lleva el nombre de un brillante matemático francés llamado Évariste Galois.
Galois creó esta teoría para entender mejor las raíces de los polinomios. Un polinomio es una expresión matemática con sumas, restas y multiplicaciones de variables elevadas a potencias, como x² + 3x - 5. Con su teoría, Galois pudo saber qué ecuaciones polinómicas se pueden resolver usando solo sumas, restas, multiplicaciones, divisiones y raíces (como la raíz cuadrada o la raíz cúbica). A estas ecuaciones se les llama "resolubles por radicales".
La teoría de Galois nos ayuda a entender por qué no existe una fórmula general para resolver ecuaciones polinómicas de quinto grado o más, usando solo radicales. Esto es una generalización del teorema de Abel-Ruffini, que ya había dicho que un polinomio general de grado cinco o más no se puede resolver así.
La teoría de Galois también ha servido para resolver problemas muy antiguos, como demostrar que no se puede "doblar el cubo" (construir un cubo con el doble de volumen de otro usando solo regla y compás) ni "trisecar el ángulo" (dividir un ángulo en tres partes iguales con regla y compás). También ayudó a describir qué polígonos regulares se pueden construir con regla y compás.
El trabajo de Galois fue publicado por Joseph Liouville catorce años después de su muerte. La teoría tardó un tiempo en ser comprendida y aceptada por otros matemáticos.
Contenido
Teoría de Galois: Descubriendo los Secretos de las Ecuaciones
La teoría de Galois es una herramienta poderosa en matemáticas. Nos ayuda a entender la estructura de las ecuaciones y sus soluciones. Es especialmente útil para saber si una ecuación se puede resolver de una manera específica.
¿Quién fue Évariste Galois?
Évariste Galois fue un matemático francés que vivió en el siglo XIX. Nació en 1811 y murió muy joven, en 1832, a los 20 años. A pesar de su corta vida, sus ideas revolucionaron las matemáticas. Sus trabajos sobre la teoría de grupos y la teoría de cuerpos sentaron las bases de lo que hoy conocemos como la teoría de Galois. Su obra fue tan avanzada que tardó años en ser completamente entendida por otros matemáticos.
¿Para qué Sirve la Teoría de Galois?
La teoría de Galois tiene varias aplicaciones importantes. Nos ayuda a responder preguntas que han intrigado a los matemáticos durante siglos.
Resolviendo Ecuaciones Polinómicas
Una de las principales razones por las que nació la teoría de Galois fue para responder a una pregunta clave: ¿Por qué no hay una fórmula general para resolver ecuaciones polinómicas de quinto grado o más, usando solo sumas, restas, multiplicaciones, divisiones y raíces?
El teorema de Abel-Ruffini, que es parte de la teoría de Galois, nos da la respuesta. Esta teoría no solo explica por qué no existe esa fórmula para grados altos, sino que también nos dice por qué sí es posible resolver ecuaciones de segundo, tercer y cuarto grado con fórmulas que usan radicales.
Problemas Clásicos de Geometría
Además de las ecuaciones, la teoría de Galois también resuelve problemas clásicos de geometría que involucran construcciones con regla y compás. Nos dice cuándo es posible construir ciertas figuras o longitudes. Por ejemplo, puede responder a estas preguntas:
- ¿Qué polígonos regulares se pueden construir usando solo regla y compás?
- ¿Por qué no es posible dividir un ángulo en tres partes iguales (trisecar un ángulo) usando solo regla y compás?
¿Cómo Funciona la Teoría de Galois? (Una Idea Sencilla)
La idea principal de la teoría de Galois es estudiar las "simetrías" de las raíces de un polinomio. Imagina que tienes las soluciones de una ecuación. La teoría de Galois mira cómo puedes "reordenar" o "permutar" esas soluciones de tal manera que las relaciones matemáticas entre ellas sigan siendo válidas.
El conjunto de todas estas permutaciones forma un "grupo de Galois". Este grupo nos da mucha información sobre la ecuación.
Ejemplo 1: Ecuaciones Cuadráticas
Tomemos una ecuación sencilla como: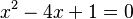 
Sus soluciones son: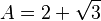 
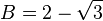Si sumamos A y B, obtenemos 4. Si los multiplicamos, obtenemos 1. Estas relaciones son ciertas. Si intercambiamos A y B, las relaciones siguen siendo válidas. Por ejemplo, B+A también es 4. El grupo de Galois para esta ecuación tiene dos "movimientos": dejar A y B como están, o intercambiarlos. Esto es como un grupo muy simple.
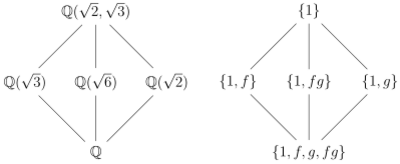
Ejemplo 2: Un Polinomio de Cuarto Grado
Consideremos el polinomio: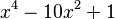 
Este polinomio tiene cuatro soluciones: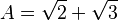 
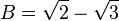
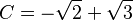Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): D = -\sqrt{2} - \sqrt{3} Hay muchas maneras de reordenar estas cuatro soluciones (24 en total). Pero el grupo de Galois solo incluye las permutaciones que mantienen válidas todas las relaciones matemáticas entre A, B, C y D. Por ejemplo, sabemos que A + D = 0. Si una permutación cambia esto, no es parte del grupo de Galois.
Al analizar todas las relaciones, se descubre que solo hay unas pocas permutaciones que cumplen la condición. Estas permutaciones forman el grupo de Galois para este polinomio.
Grupos Solubles y Soluciones por Radicales
Un concepto clave en la teoría de Galois es el de "grupo resoluble" (o soluble). La teoría de Galois nos dice que una ecuación polinómica se puede resolver usando radicales (es decir, con fórmulas que incluyen raíces) si y solo si su grupo de Galois es un grupo resoluble.
Los grupos de Galois de los polinomios de grado cuatro o menos siempre son resolubles. Por eso, siempre podemos encontrar una fórmula con radicales para ellos. Sin embargo, para polinomios de grado cinco o más, el grupo de Galois no siempre es resoluble. Esto explica por qué no hay una fórmula general para resolverlos.
El Problema Inverso de Galois
Existe un problema abierto en matemáticas llamado el "problema inverso de Galois". La pregunta es si cualquier grupo finito puede ser el grupo de Galois de alguna ecuación con números racionales como coeficientes. Este problema fue propuesto por David Hilbert en el siglo XIX y aún no tiene una respuesta definitiva.
Véase también
En inglés: Galois theory Facts for Kids
- teoría de ecuaciones
