Raíz de una función para niños
Si buscas la raíz enésima de un número, ve a Función raíz.
En matemática, una raíz de un polinomio o un cero de una función es un valor especial. Imagina que tienes una función, como una máquina matemática que toma un número y te da otro. Una raíz es el número que, cuando lo pones en esa máquina, hace que el resultado sea cero.
Se escribe así:
.
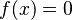Aquí, f(x) representa la función, y x es el valor que estamos buscando.
Por ejemplo, si tenemos la función:
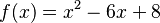
Para encontrar sus raíces, necesitamos saber qué valor de x hace que f(x) sea igual a cero. Esto se convierte en una ecuación:
Si pruebas con los números 2 y 4, verás que ambos hacen que la ecuación sea cierta:
- Si x = 2, entonces f(2) = 2² - 6(2) + 8 = 4 - 12 + 8 = 0.
- Si x = 4, entonces f(4) = 4² - 6(4) + 8 = 16 - 24 + 8 = 0.
Así, 2 y 4 son las raíces de esta función.
Contenido
¿Cómo encontrar las raíces de una función?
La conexión entre raíces y gráficos
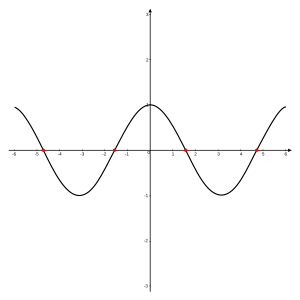
Cuando dibujas el gráfico de una función en un plano de coordenadas cartesianas, las raíces son los puntos donde el gráfico cruza o toca el eje horizontal (el eje de las abscisas). Es como si el gráfico "cortara" el eje justo en esos valores de x donde la función vale cero.
El Teorema Fundamental del Álgebra
Hay un teorema muy importante en matemáticas llamado el teorema fundamental del álgebra. Este teorema nos dice que cualquier polinomio (una expresión matemática con sumas y restas de términos con potencias de una variable, como x² + 3x - 5) de grado n (donde n es la potencia más alta de la variable) tiene exactamente n raíces. Algunas de estas raíces pueden ser números "normales" (reales), y otras pueden ser números "imaginarios" o "complejos".
Por ejemplo, un polinomio de grado 2 (como x² - 6x + 8) tendrá 2 raíces. Un polinomio de grado 3 tendrá 3 raíces, y así sucesivamente.
Raíces en funciones especiales
Algunas funciones pueden tener muchas raíces, incluso infinitas. Por ejemplo, la función seno (escrita como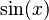 
) tiene infinitas raíces. Esto significa que cruza el eje horizontal una y otra vez.
Por otro lado, hay funciones que nunca tienen raíces. Por ejemplo, la función exponencial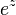 
nunca es igual a cero, sin importar qué valor le des a z.
Métodos para buscar raíces de forma aproximada
A veces, encontrar las raíces exactas de una función es muy difícil o imposible. En esos casos, los matemáticos y científicos usan métodos numéricos para encontrar raíces de forma aproximada. Estos métodos son como "recetas" paso a paso que nos ayudan a acercarnos cada vez más al valor real de la raíz. Algunos de estos métodos son:
- Método de Newton-Raphson
- Método de la secante
- Método de bisección del intervalo
Raíces simples y múltiples
Cuando una función tiene una raíz, podemos escribir la función de una manera especial. Si r es una raíz de la función f, podemos escribir f(x) como:
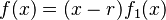
Aquí, f_1(x) es otra función.
- Una raíz es simple si, al reemplazar x por r en f_1(x), el resultado no es cero (
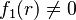). Esto significa que el gráfico de la función cruza el eje horizontal en ese punto. - Una raíz es múltiple si, al reemplazar x por r en f_1(x), el resultado es cero (
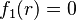). Esto significa que el gráfico de la función toca el eje horizontal en ese punto, pero no lo cruza, o lo cruza de una manera especial. Si una raíz es múltiple, se dice que tiene un "orden". Por ejemplo, una raíz de orden 2 significa que el factor (x-r) aparece dos veces en la función.
Galería de imágenes
-
Las raíces de la función ƒ(x)=cosx en el gráfico están marcadas en rojo. Son los puntos donde la línea azul cruza el eje horizontal (eje x).
Véase también
En inglés: Zero of a function Facts for Kids
