Grupo (matemática) para niños

En álgebra abstracta, un grupo es un concepto matemático que nos ayuda a entender cómo funcionan ciertas colecciones de cosas cuando las combinamos de una manera específica. Imagina un conjunto de elementos y una forma de unirlos, como sumar números o girar un objeto. Si esa forma de unirlos cumple con ciertas reglas, entonces tenemos un grupo.

Los grupos son muy importantes en las matemáticas y en otras ciencias. Nos ayudan a describir patrones y simetrías en muchos lugares, desde la forma en que se mueven los objetos hasta las leyes de la física.

¿Qué es un grupo? Un ejemplo sencillo

El grupo de los números enteros con la suma

Uno de los ejemplos más fáciles de entender es el de los números enteros (..., -3, -2, -1, 0, 1, 2, 3, ...). Si usamos la suma como nuestra forma de combinar los números, veremos que cumplen las reglas de un grupo:

• Cerrado: Si sumas dos números enteros, el resultado siempre es otro número entero. Por ejemplo, 3 + 5 = 8.
• Asociativo: No importa cómo agrupes los números al sumar. Por ejemplo, (2 + 3) + 4 es lo mismo que 2 + (3 + 4). El resultado siempre es 9.
• Elemento neutro: Existe un número especial, el cero (0), que al sumarlo a cualquier otro número, no lo cambia. Por ejemplo, 7 + 0 = 7.
• Elemento inverso: Para cada número entero, existe otro número que, al sumarlo, da como resultado el cero. Por ejemplo, el inverso de 5 es -5, porque 5 + (-5) = 0.

Estas cuatro reglas son la base para definir un grupo. La teoría de grupos es la rama de las matemáticas que estudia estas estructuras.

Definición formal de un grupo

Para que un conjunto 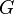con una operación 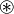sea un grupo, debe cumplir estas reglas (llamadas axiomas):

1. Operación interna: Cuando combinas dos elementos de 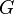usando 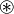, el resultado siempre debe estar también en .
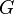2. Asociatividad: Si tienes tres elementos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g, h, k en 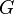, no importa cómo los agrupes: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (g \circledast h) \circledast k = g \circledast (h \circledast k) .
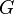3. Elemento neutro: Debe existir un elemento especial, llamado (o identidad), en que, al combinarlo con cualquier otro elemento 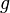, no lo cambia: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e \circledast g = g \circledast e = g .
4. Elemento inverso: Para cada elemento 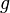en 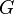, debe existir otro elemento 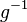(su inverso) en 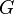tal que al combinarlos, el resultado sea el elemento neutro: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g \circledast g^{-1} = g^{-1} \circledast g = e .

Si además de estas reglas, el orden en que combinas los elementos no importa (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g \circledast h = h \circledast g ), se dice que el grupo es abeliano o conmutativo. El grupo de los números enteros con la suma es un grupo abeliano.

Historia y desarrollo de los grupos

El estudio de los grupos comenzó en el siglo XIX, con matemáticos como Évariste Galois. Él los usó para entender las soluciones de ecuaciones complicadas. Más tarde, otros matemáticos como Ferdinand Georg Frobenius definieron los grupos de forma más general, usando los axiomas que conocemos hoy.

La teoría de grupos moderna es un campo muy activo. Los matemáticos buscan entender cómo se comportan los grupos, dividiéndolos en partes más pequeñas y estudiando sus propiedades. También investigan cómo los grupos se pueden usar para describir cosas reales, como las simetrías.

Los grupos y las simetrías: aplicaciones

La idea de grupo está muy relacionada con la simetría. Un grupo de simetría nos dice qué transformaciones (como rotaciones o reflejos) dejan un objeto sin cambios.

• En física, los grupos ayudan a entender las leyes fundamentales, como las de la relatividad y la física de partículas.
• En química, se usan para estudiar la simetría molecular y atómica.
• En geología, son importantes en la cristalografía, que estudia la estructura de los cristales.

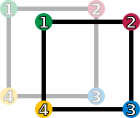
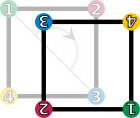
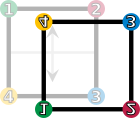
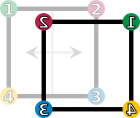
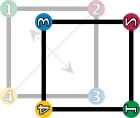
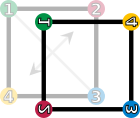
Un grupo de simetría: el cuadrado

Las simetrías de un cuadrado forman un grupo llamado grupo diédrico, 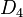. Un cuadrado tiene ocho simetrías:

id (no se mueve)	r1 (rotación de 90° a la derecha)	r2 (rotación de 180° a la derecha)	r3 (rotación de 270° a la derecha)
fv (voltear verticalmente)	fh (voltear horizontalmente)	fd (voltear por diagonal)	fc (voltear por contra diagonal)
Los elementos del grupo de simetría del cuadrado (). Los vértices están marcados para ver los movimientos.

• La operación identidad (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \text{id} ) deja el cuadrado exactamente como estaba.
• Las rotaciones (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): r_1, r_2, r_3 ) giran el cuadrado 90°, 180° o 270° a la derecha.
• Las reflexiones (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f_v, f_h, f_d, f_c ) son como voltear el cuadrado por una línea (eje vertical, horizontal o diagonal).

Si combinas cualquiera de estas operaciones (por ejemplo, girar 90° y luego voltear verticalmente), el resultado es otra de las ocho simetrías. Esto demuestra que forman un grupo.

Cómo se escriben los grupos

En matemáticas, se usan símbolos especiales para hablar de los grupos:

• El conjunto se suele llamar 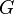(de Grupo).
• La operación se puede representar con símbolos com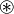o , o .
• Los elementos del grupo se escriben con letras minúsculas (a, b, c).
• El elemento neutro se llama (o 0 si es una suma, o 1 si es una multiplicación).
• El elemento inverso de se escribe 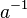(o 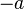si es una suma).

Conceptos importantes de los grupos

Propiedades básicas

De las reglas de los grupos, podemos deducir algunas cosas importantes:

• El elemento neutro de un grupo es único. Solo hay uno.
• Cada elemento de un grupo tiene un elemento inverso único.
• Si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ac = bc o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ab = ac en un grupo, entonces podemos "cancelar" y decir que o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b=c .

Subgrupos

Un subgrupo es un conjunto más pequeño dentro de un grupo grande que también cumple todas las reglas para ser un grupo con la misma operación. Es como una "mini-grupo" dentro del grupo principal.

Orden de un grupo y sus elementos

• El orden de un grupo es la cantidad de elementos que tiene. Si tiene un número finito de elementos, es un grupo finito.
• El orden de un elemento es el número de veces que tienes que combinarlo consigo mismo para obtener el elemento neutro. Si nunca lo obtienes, el elemento tiene orden infinito.

Un teorema importante, el teorema de Lagrange, dice que el orden de cualquier subgrupo de un grupo finito siempre divide al orden del grupo.

Homomorfismos de grupos

Un homomorfismo es una función que "conecta" dos grupos de una manera especial. Si tienes dos grupos, 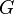y 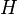, un homomorfismo 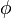es una función de 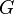a 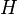que mantiene la estructura. Esto significa que si combinas dos elementos en 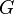y luego aplicas 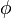, es lo mismo que aplicar 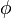a cada elemento por separado y luego combinarlos en .

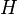Si un homomorfismo es "perfecto" (es decir, cada elemento de 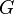se conecta con un único elemento de 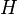y viceversa), se llama isomorfismo. Dos grupos que son isomorfos son, en esencia, el mismo grupo, solo que sus elementos pueden tener nombres diferentes.

Ejemplos de grupos importantes

Además del grupo de los números enteros con la suma, hay muchos otros grupos:

• Los grupos de la suma de números racionales, números reales y números complejos.
• Los grupos de la suma de vectores.
• Los grupos de la suma de matrices.
• Los grupos de las horas en un reloj (por ejemplo, en un reloj de 12 horas, 12 es el elemento neutro, y 12 + 1 = 1).
• Los grupos de la multiplicación de números racionales, reales y complejos (sin incluir el cero, porque no tiene inverso multiplicativo).
• Las matrices cuadradas que se pueden invertir forman un grupo con la multiplicación de matrices. Este grupo no es conmutativo.
• El Cubo de Rubik es un ejemplo de un grupo. Cada movimiento que haces en el cubo es un elemento del grupo, y combinar movimientos es la operación.

Las posibles manipulaciones del Cubo de Rubik forman un grupo.

Tipos de grupos

Los grupos se pueden clasificar de muchas maneras:

• Grupos finitos: Tienen un número limitado de elementos.
• Grupos infinitos: Tienen un número ilimitado de elementos.
• Grupos cíclicos: Son grupos que pueden ser generados por un solo elemento. Es decir, si tomas ese elemento y lo combinas consigo mismo repetidamente, puedes obtener todos los demás elementos del grupo. El grupo de los números enteros con la suma es cíclico, generado por el 1 (o el -1).
• Grupos abelianos (o conmutativos): Aquellos en los que el orden de la operación no importa (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a \circledast b = b \circledast a ).
• Grupos topológicos: Son grupos que también tienen una estructura de espacio, donde las operaciones son "suaves" o continuas.
• Grupos de Lie: Son un tipo especial de grupos topológicos que son muy importantes en física y geometría.
• Grupos simples: Son grupos que no tienen subgrupos "normales" propios. Son como los "bloques de construcción" más básicos de los grupos.

Galería de imágenes

• 

  Construcción de estructuras algebraicas: desde un magma hasta un grupo, añadiendo propiedades como asociatividad, elemento neutro e inversos.

Véase también

En inglés: Group (mathematics) Facts for Kids