Multiplicación para niños
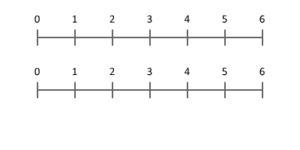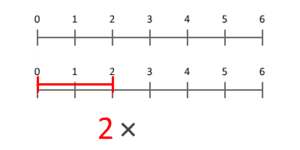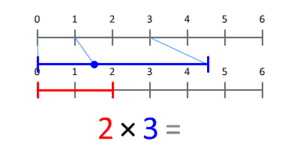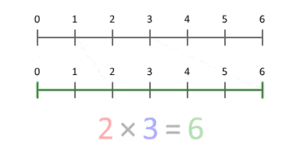
La multiplicación es una operación matemática fundamental. Es como una forma rápida de hacer una suma repetida. Imagina que tienes 3 grupos de 4 manzanas. En lugar de sumar 4 + 4 + 4, puedes multiplicar 3 × 4 para obtener el total de 12 manzanas.
Es una de las cuatro operaciones básicas en aritmética, junto con la suma, la resta y la división. La multiplicación es la operación opuesta a la división. Por ejemplo, si 5 × 2 = 10, entonces 10 ÷ 2 = 5 y 10 ÷ 5 = 2.
Contenido
¿Qué es la Multiplicación?
La multiplicación consiste en sumar una cantidad varias veces, según lo indique otro número. Por ejemplo, 4 × 3 significa sumar el número 4, tres veces: 4 + 4 + 4, lo que da 12. También puedes verlo como 3 filas de 4 objetos, o 4 filas de 3 objetos.
Los números que multiplicamos se llaman factores. El resultado de la multiplicación se llama producto. En el ejemplo 4 × 3 = 12, el 4 y el 3 son los factores, y el 12 es el producto.
La multiplicación también nos ayuda a calcular el área de un rectángulo. Si multiplicas el largo por el ancho, obtendrás la superficie que cubre.
Puedes multiplicar dos o más números. El orden en que los multipliques no cambia el resultado. Por ejemplo:
- 3 × 4 × 5 = 60
- 5 × 3 × 4 = 60
- 4 × 5 × 3 = 60
Potenciación: Multiplicación Especial
La potenciación es un tipo especial de multiplicación. Aquí, un número se multiplica por sí mismo varias veces. El número que se multiplica se llama base, y la cantidad de veces que se multiplica se llama exponente.
Por ejemplo, 26 significa 2 multiplicado por sí mismo 6 veces: 2 × 2 × 2 × 2 × 2 × 2 = 64. En este caso, 2 es la base y 6 es el exponente.
¿Cómo se escribe la Multiplicación?
Existen varias formas de escribir una multiplicación:
- El signo "×" (una cruz). Por ejemplo, 3 × 4.
- Un punto medio "•". Por ejemplo, 3 • 4.
- En álgebra, cuando usamos letras (variables), a menudo se omite el signo. Por ejemplo, "3ab" significa 3 multiplicado por "a" y por "b". "xy" significa "x" multiplicado por "y".
- También se pueden usar paréntesis para agrupar números, especialmente con números negativos. Por ejemplo, (3)(4) o 3(4).
Notación con Puntos Suspensivos
Cuando tienes una lista larga de números para multiplicar, puedes usar puntos suspensivos (...) para mostrar que hay números intermedios. Por ejemplo, el producto de todos los números del 1 al 100 se puede escribir: 1 • 2 • ... • 99 • 100
El Símbolo Productorio
Para productos muy largos o con una regla específica, se usa el símbolo productorio, que es la letra griega Pi mayúscula (Π). Se ve así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \prod_{i=m}^{n} x_{i} Esto significa que multiplicas todos los valores de  desde un valor inicial (
desde un valor inicial (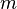 ) hasta un valor final (
) hasta un valor final ( ).
).
Multiplicación de Diferentes Tipos de Números
La multiplicación funciona de manera similar para diferentes tipos de números:
Multiplicación de Números Enteros
Los números enteros incluyen los números positivos, negativos y el cero.
- Si ambos factores son positivos (como 3 × 5), el resultado es positivo (15).
- Si ambos factores son negativos (como -3 × -5), el resultado es positivo (15).
- Si un factor es positivo y el otro es negativo (como -3 × 5 o 3 × -5), el resultado es negativo (-15).
- Si uno de los factores es cero (como 3 × 0 o -5 × 0), el resultado siempre es cero.
Multiplicación de Fracciones
Para multiplicar fracciones, multiplicas los números de arriba (numeradores) entre sí y los números de abajo (denominadores) entre sí.
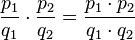
Multiplicación de Raíces
Una propiedad importante de las raíces es que la raíz de un producto es igual al producto de las raíces. ![\sqrt[n]{{a} \cdot {b}} = \sqrt[n]{a} \cdot \sqrt[n]{b}](/images/math/6/2/f/62ff232d8ae597f13efb5db26edc04cb.png)
Propiedades Importantes de la Multiplicación
La multiplicación tiene varias propiedades que la hacen predecible y útil:
Propiedad de Cerradura
Cuando multiplicas dos números naturales, el resultado siempre será otro número natural.
- Ejemplo: 3 × 2 = 6 (3, 2 y 6 son números naturales).
Propiedad Conmutativa
El orden de los factores no cambia el producto. Puedes cambiar el orden y el resultado será el mismo.
- Ejemplo: 3 × 4 = 12 y 4 × 3 = 12.
Propiedad Asociativa
Si tienes tres o más números multiplicándose, no importa cómo los agrupes con paréntesis, el resultado será el mismo.
- Ejemplo: (2 × 3) × 4 = 6 × 4 = 24. También 2 × (3 × 4) = 2 × 12 = 24.
Propiedad Distributiva
Esta propiedad conecta la multiplicación con la suma. Si multiplicas un número por una suma, es lo mismo que multiplicar el número por cada parte de la suma y luego sumar los resultados.
- Ejemplo: 2 × (3 + 4) = 2 × 7 = 14.
- También: (2 × 3) + (2 × 4) = 6 + 8 = 14.
Elemento Identidad (Neutro)
El número 1 es el elemento identidad de la multiplicación. Cualquier número multiplicado por 1 es igual a sí mismo.
- Ejemplo: 7 × 1 = 7.
Elemento Cero (Absorbente)
El número 0 es el elemento absorbente. Cualquier número multiplicado por 0 da como producto 0.
- Ejemplo: 5 × 0 = 0.
Negación
- Multiplicar cualquier número por -1 da como resultado el opuesto de ese número.
* Ejemplo: (-1) × 5 = -5.
- Multiplicar -1 por -1 da como resultado 1.
* Ejemplo: (-1) × (-1) = 1.
Elemento Inverso
Para cualquier número x (excepto el cero), existe un inverso multiplicativo (también llamado recíproco), que es 1 dividido por ese número ( ). Cuando multiplicas un número por su inverso, el resultado es 1.
). Cuando multiplicas un número por su inverso, el resultado es 1.
- Ejemplo: 5 × Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1}{5} = 1.
Conexión con la Geometría
La multiplicación tiene una relación directa con la geometría.
- Multiplicar dos valores (como largo por ancho) nos da un área.
- Multiplicar tres valores (como largo por ancho por alto) nos da un volumen.
Véase también
 En inglés: Multiplication Facts for Kids
En inglés: Multiplication Facts for Kids