Adición (matemática) para niños
La adición o suma es una operación matemática fundamental. Consiste en combinar o añadir dos o más números para obtener una cantidad final, que llamamos el total. Imagina que tienes dos grupos de objetos y los juntas todos en uno solo; la suma te dice cuántos objetos tienes en total. Sumar "uno" repetidamente es la forma más básica de contar.
La suma se usa con diferentes tipos de números, como los números naturales (1, 2, 3...), los números enteros (..., -1, 0, 1, ...), los números racionales (fracciones), los números reales (con decimales) y los números complejos. También se aplica en otras áreas de las matemáticas, como cuando sumamos matrices o vectores.
Contenido
Historia de la Suma
¿Desde cuándo sumamos?
Los seres humanos han sumado desde hace mucho tiempo. Incluso el hombre del neolítico (una etapa antigua de la humanidad) ya realizaba cálculos básicos. Aunque no lo creas, es posible que primero entendieran la idea de "restar", porque veían cómo sus alimentos disminuían con el tiempo.
La suma a través de las civilizaciones
- Los egipcios fueron capaces de sumar números naturales y también fracciones.
- Los babilonios sumaban los cuadrados de los números.
- En China y la India, se empezó a trabajar con los números negativos.
- Durante el Renacimiento, con el crecimiento del comercio y la banca, se hizo muy importante sumar decimales. También se usaban los logaritmos para simplificar multiplicaciones grandes en áreas como el comercio y la navegación.
Con el tiempo, la suma se adaptó a diferentes tipos de números, como los números reales (con decimales) y los números complejos.
Propiedades Clave de la Suma
La suma tiene algunas reglas o propiedades que siempre se cumplen, especialmente con los números naturales, números enteros, números racionales y números reales.
Propiedad Conmutativa
Esta propiedad significa que el orden en que sumas los números no cambia el resultado.
- Ejemplo: 2 + 3 es lo mismo que 3 + 2. Ambos dan 5.
- En matemáticas:
 .
.
Propiedad Asociativa
Cuando sumas tres o más números, puedes agruparlos de diferentes maneras y el resultado será el mismo.
- Ejemplo: (2 + 3) + 4 es lo mismo que 2 + (3 + 4).
* (2 + 3) + 4 = 5 + 4 = 9 * 2 + (3 + 4) = 2 + 7 = 9
- En matemáticas:
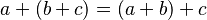 .
.
Propiedad Distributiva
Esta propiedad relaciona la suma con la multiplicación. Si sumas dos números y luego multiplicas el resultado por un tercer número, es lo mismo que multiplicar cada uno de los dos primeros números por el tercero y luego sumar esos productos.
- Ejemplo: (3 + 4) × 6 = 3 × 6 + 4 × 6
* (3 + 4) × 6 = 7 × 6 = 42 * 3 × 6 + 4 × 6 = 18 + 24 = 42
- En matemáticas: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (a+b)\cdot c=a\cdot c+b\cdot c .
Elemento Neutro (Cero)
El cero es el "elemento neutro" de la suma. Esto significa que cualquier número sumado con cero da como resultado el mismo número.
- Ejemplo: 5 + 0 = 5.
- En matemáticas:
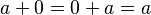 .
.
Elemento Opuesto (Inverso Aditivo)
Para cada número, existe otro número (su opuesto) que, al sumarse, da como resultado cero. Esto es especialmente útil con los números enteros (positivos y negativos).
- Ejemplo: 7 + (-7) = 0.
- En matemáticas: Si
 es un número, existe
es un número, existe 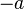 tal que
tal que 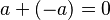 .
.
El Símbolo de Suma (Sumatorio)
Sumas con el signo "+"
Cuando sumamos pocos números, usamos el símbolo "+" (leído "más").
- Ejemplo: 1 + 2 + 4 = 7.
También usamos el "+" cuando hay muchos números, pero se entiende cuáles son los que faltan, usando puntos suspensivos (...).
- Ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1+2+3+\cdots+100 es la suma de los primeros cien números naturales.
El símbolo "Σ" (Sigma)
Para sumas muy largas o infinitas, usamos un símbolo especial llamado "sumatorio", que es la letra griega sigma mayúscula (Σ).
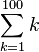 significa "sumar todos los números desde k=1 hasta k=100". Es lo mismo que 1 + 2 + 3 + ... + 100.
significa "sumar todos los números desde k=1 hasta k=100". Es lo mismo que 1 + 2 + 3 + ... + 100.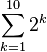 significa "sumar las potencias de 2 desde k=1 hasta k=10". Es lo mismo que 2¹ + 2² + ... + 2¹⁰.
significa "sumar las potencias de 2 desde k=1 hasta k=10". Es lo mismo que 2¹ + 2² + ... + 2¹⁰.
Cómo Realizar una Suma Larga
Para sumar varios números grandes, los colocamos uno debajo del otro, alineando las cifras por su valor posicional: unidades (U), decenas (D), centenas (C), millares (M), etc., empezando por la derecha.
Veamos un ejemplo: 750 + 1583 + 69.
1. Alinear los números:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{rrrrr} & M & C & D & U \\ & & 7 & 5 & 0 \\ & 1 & 5 & 8 & 3 \\ + & & & 6 & 9 \\ \hline \end{array} \begin{array}{l} \\ \longleftarrow 1^{\circ} \; \textrm{sumando}\\ \longleftarrow 2^{\circ} \; \textrm{sumando}\\ \longleftarrow 3^{\circ} \; \textrm{sumando}\\ \end{array}
2. Sumar las unidades: Sumamos los números de la columna de las unidades (derecha). * 0 + 3 + 9 = 12. * Escribimos el "2" debajo de la columna de unidades y "llevamos" el "1" (de las decenas) a la siguiente columna.
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{rrrrr} & & & 1 & \\ & M & C & D & U \\ & & 7 & 5 & 0 \\ & 1 & 5 & 8 & 3 \\ + & & & 6 & 9 \\ \hline & & & & 2 \\ \end{array} \begin{array}{l} { \color{Red}\longleftarrow \textrm{acarreo} }\\ \\ \longleftarrow 1^{\circ} \; \textrm{sumando}\\ \longleftarrow 2^{\circ} \; \textrm{sumando}\\ \longleftarrow 3^{\circ} \; \textrm{sumando}\\ \\ \end{array}
3. Sumar las decenas: Sumamos los números de la columna de las decenas, incluyendo el "1" que llevamos. * 1 (acarreo) + 5 + 8 + 6 = 20. * Escribimos el "0" debajo de la columna de decenas y "llevamos" el "2" a la siguiente columna.
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{rrrrr} & & 2 & 1 & \\ & M & C & D & U \\ & & 7 & 5 & 0 \\ & 1 & 5 & 8 & 3 \\ + & & & 6 & 9 \\ \hline & & & 0 & 2 \\ \end{array} \begin{array}{l} { \color{Red}\longleftarrow \textrm{acarreo} }\\ \\ \longleftarrow 1^{\circ} \; \textrm{sumando}\\ \longleftarrow 2^{\circ} \; \textrm{sumando}\\ \longleftarrow 3^{\circ} \; \textrm{sumando}\\ \\ \end{array}
4. Sumar las centenas: Sumamos los números de la columna de las centenas, incluyendo el "2" que llevamos. * 2 (acarreo) + 7 + 5 = 14. * Escribimos el "4" debajo de la columna de centenas y "llevamos" el "1" a la siguiente columna.
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{rrrrr} & 1 & 2 & 1 & \\ & M & C & D & U \\ & & 7 & 5 & 0 \\ & 1 & 5 & 8 & 3 \\ + & & & 6 & 9 \\ \hline & & 4 & 0 & 2 \\ \end{array} \begin{array}{l} { \color{Red}\longleftarrow \textrm{acarreo} }\\ \\ \longleftarrow 1^{\circ} \; \textrm{sumando}\\ \longleftarrow 2^{\circ} \; \textrm{sumando}\\ \longleftarrow 3^{\circ} \; \textrm{sumando}\\ \\ \end{array}
5. Sumar los millares: Sumamos los números de la columna de los millares, incluyendo el "1" que llevamos. * 1 (acarreo) + 1 = 2. * Escribimos el "2" debajo de la columna de millares. Como no hay más columnas, este es el resultado final.
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{rrrrr} & 1 & 2 & 1 & \\ & M & C & D & U \\ & & 7 & 5 & 0 \\ & 1 & 5 & 8 & 3 \\ + & & & 6 & 9 \\ \hline & 2 & 4 & 0 & 2 \\ \end{array} \begin{array}{l} { \color{Red}\longleftarrow \textrm{acarreo} }\\ \\ \longleftarrow 1^{\circ} \; \textrm{sumando}\\ \longleftarrow 2^{\circ} \; \textrm{sumando}\\ \longleftarrow 3^{\circ} \; \textrm{sumando}\\ \longleftarrow \textrm{total}\\ \end{array}
El resultado de 750 + 1583 + 69 es 2402.
Suma con Diferentes Tipos de Números
Suma de Números Enteros
- Si los números tienen el mismo signo (ambos positivos o ambos negativos), sumas sus valores y mantienes el signo.
* Ejemplo: 3 + 5 = 8. * Ejemplo: (-3) + (-5) = -8.
- Si los números tienen signos diferentes (uno positivo y uno negativo), restas el valor más pequeño del valor más grande. El resultado tendrá el signo del número con el valor más grande.
* Ejemplo: 8 + (-3) = 5 (porque 8 es mayor que 3 y 8 es positivo). * Ejemplo: (-8) + 3 = -5 (porque 8 es mayor que 3 y -8 es negativo).
Suma de Números Racionales (Fracciones)
- Mismo denominador: Si las fracciones tienen el mismo número abajo (denominador), solo sumas los números de arriba (numeradores) y mantienes el mismo denominador.
* Ejemplo: 1/4 + 2/4 = 3/4.
- Diferentes denominadores: Si tienen denominadores diferentes, primero debes encontrar un denominador común para todas las fracciones. Luego, ajustas los numeradores y sumas como si tuvieran el mismo denominador.
* Ejemplo: 1/2 + 1/3. El denominador común es 6. * 1/2 se convierte en 3/6. * 1/3 se convierte en 2/6. * Entonces, 3/6 + 2/6 = 5/6.
Tablas de Sumar
Las tablas de sumar nos ayudan a recordar rápidamente los resultados de las sumas básicas.
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{c} \text{Tabla de sumar} \\ \\ \begin{array}{ccccc} \begin{array}{|c|} \hline \text{Tabla del 1} \\ \begin{array}{rcrcr} 0 & + & 1 & = & 1 \\ 1 & + & 1 & = & 2 \\ 2 & + & 1 & = & 3 \\ 3 & + & 1 & = & 4 \\ 4 & + & 1 & = & 5 \\ 5 & + & 1 & = & 6 \\ 6 & + & 1 & = & 7 \\ 7 & + & 1 & = & 8 \\ 8 & + & 1 & = & 9 \\ 9 & + & 1 & = & 10 \\ 10 & + & 1 & = & 11 \\ \end{array} \\ \hline \end{array} & \begin{array}{|c|} \hline \text{Tabla del 2} \\ \begin{array}{rcrcr} 0 & + & 2 & = & 2 \\ 1 & + & 2 & = & 3 \\ 2 & + & 2 & = & 4 \\ 3 & + & 2 & = & 5 \\ 4 & + & 2 & = & 6 \\ 5 & + & 2 & = & 7 \\ 6 & + & 2 & = & 8 \\ 7 & + & 2 & = & 9 \\ 8 & + & 2 & = & 10 \\ 9 & + & 2 & = & 11 \\ 10 & + & 2 & = & 12 \\ \end{array} \\ \hline \end{array} & \begin{array}{|c|} \hline \text{Tabla del 3} \\ \begin{array}{rcrcr} 0 & + & 3 & = & 3 \\ 1 & + & 3 & = & 4 \\ 2 & + & 3 & = & 5 \\ 3 & + & 3 & = & 6 \\ 4 & + & 3 & = & 7 \\ 5 & + & 3 & = & 8 \\ 6 & + & 3 & = & 9 \\ 7 & + & 3 & = & 10 \\ 8 & + & 3 & = & 11 \\ 9 & + & 3 & = & 12 \\ 10 & + & 3 & = & 13 \\ \end{array} \\ \hline \end{array} & \begin{array}{|c|} \hline \text{Tabla del 4} \\ \begin{array}{rcrcr} 0 & + & 4 & = & 4 \\ 1 & + & 4 & = & 5 \\ 2 & + & 4 & = & 6 \\ 3 & + & 4 & = & 7 \\ 4 & + & 4 & = & 8 \\ 5 & + & 4 & = & 9 \\ 6 & + & 4 & = & 10 \\ 7 & + & 4 & = & 11 \\ 8 & + & 4 & = & 12 \\ 9 & + & 4 & = & 13 \\ 10 & + & 4 & = & 14 \\ \end{array} \\ \hline \end{array} & \begin{array}{|c|} \hline \text{Tabla del 5} \\ \begin{array}{rcrcr} 0 & + & 5 & = & 5 \\ 1 & + & 5 & = & 6 \\ 2 & + & 5 & = & 7 \\ 3 & + & 5 & = & 8 \\ 4 & + & 5 & = & 9 \\ 5 & + & 5 & = & 10 \\ 6 & + & 5 & = & 11 \\ 7 & + & 5 & = & 12 \\ 8 & + & 5 & = & 13 \\ 9 & + & 5 & = & 14 \\ 10 & + & 5 & = & 15 \\ \end{array} \\ \hline \end{array} \\ \\ \begin{array}{|c|} \hline \text{Tabla del 6} \\ \begin{array}{rcrcr} 0 & + & 6 & = & 6 \\ 1 & + & 6 & = & 7 \\ 2 & + & 6 & = & 8 \\ 3 & + & 6 & = & 9 \\ 4 & + & 6 & = & 10 \\ 5 & + & 6 & = & 11 \\ 6 & + & 6 & = & 12 \\ 7 & + & 6 & = & 13 \\ 8 & + & 6 & = & 14 \\ 9 & + & 6 & = & 15 \\ 10 & + & 6 & = & 16 \\ \end{array} \\ \hline \end{array} & \begin{array}{|c|} \hline \text{Tabla del 7} \\ \begin{array}{rcrcr} 0 & + & 7 & = & 7 \\ 1 & + & 7 & = & 8 \\ 2 & + & 7 & = & 9 \\ 3 & + & 7 & = & 10 \\ 4 & + & 7 & = & 11 \\ 5 & + & 7 & = & 12 \\ 6 & + & 7 & = & 13 \\ 7 & + & 7 & = & 14 \\ 8 & + & 7 & = & 15 \\ 9 & + & 7 & = & 16 \\ 10 & + & 7 & = & 17 \\ \end{array} \\ \hline \end{array} & \begin{array}{|c|} \hline \text{Tabla del 8} \\ \begin{array}{rcrcr} 0 & + & 8 & = & 8 \\ 1 & + & 8 & = & 9 \\ 2 & + & 8 & = & 10 \\ 3 & + & 8 & = & 11 \\ 4 & + & 8 & = & 12 \\ 5 & + & 8 & = & 13 \\ 6 & + & 8 & = & 14 \\ 7 & + & 8 & = & 15 \\ 8 & + & 8 & = & 16 \\ 9 & + & 8 & = & 17 \\ 10 & + & 8 & = & 18 \\ \end{array} \\ \hline \end{array} & \begin{array}{|c|} \hline \text{Tabla del 9} \\ \begin{array}{rcrcr} 0 & + & 9 & = & 9 \\ 1 & + & 9 & = & 10 \\ 2 & + & 9 & = & 11 \\ 3 & + & 9 & = & 12 \\ 4 & + & 9 & = & 13 \\ 5 & + & 9 & = & 14 \\ 6 & + & 9 & = & 15 \\ 7 & + & 9 & = & 16 \\ 8 & + & 9 & = & 17 \\ 9 & + & 9 & = & 18 \\ 10 & + & 9 & = & 19 \\ \end{array} \\ \hline \end{array} & \begin{array}{|c|} \hline \text{Tabla del 10} \\ \begin{array}{rcrcr} 0 & + & 10 & = & 10 \\ 1 & + & 10 & = & 11 \\ 2 & + & 10 & = & 12 \\ 3 & + & 10 & = & 13 \\ 4 & + & 10 & = & 14 \\ 5 & + & 10 & = & 15 \\ 6 & + & 10 & = & 16 \\ 7 & + & 10 & = & 17 \\ 8 & + & 10 & = & 18 \\ 9 & + & 10 & = & 19 \\ 10 & + & 10 & = & 20 \\ \end{array} \\ \hline \end{array} \\ \end{array} \\ \end{array>
La Suma en la Educación
La suma es una de las primeras operaciones matemáticas que aprendemos. Es muy importante porque nos ayuda a entender el concepto de número y es la base para otras operaciones más complejas. Los niños aprenden a sumar a través de varias etapas:
- Etapa 1 (antes de los 3 años): Los niños manipulan objetos, los juntan y los agrupan. Por ejemplo, si hay cubos esparcidos, pueden reunirlos todos.
- Etapa 2 (3 años): La acción de juntar objetos se acompaña de palabras. Aunque aún no entienden el concepto de número de forma abstracta, cuentan mientras realizan la acción. Por ejemplo, en un juego, si se les dice "toma 1", lo hacen y lo cuentan.
- Etapa 3 (4 años): Los niños pueden describir la acción sin necesidad de tener los objetos. Pueden decir: "Tengo 1 juguete y mi mamá me regala 1, ahora tengo 2 juguetes".
- Etapa 4 (5 años): En esta etapa, los niños ya comprenden el concepto de suma y pueden hacer operaciones sin necesidad de ver o tocar los objetos.
Estas etapas ayudan a los niños a entender la suma de forma natural y concreta, basándose en la idea de "añadir" o "juntar" cantidades.
Véase también
 En inglés: Addition Facts for Kids
En inglés: Addition Facts for Kids


