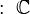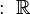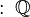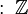Número racional para niños
Los números racionales son todos los números que se pueden escribir como una fracción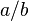 
. En esta fracción, 
es un número entero (puede ser positivo, negativo o cero) y 
es un número natural positivo (un número entero mayor que cero).
La palabra "racional" viene de "razón" o "cociente", que es el resultado de una división. El conjunto de los números racionales se representa con la letra Q (o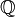 
), que viene de la palabra "cociente" en latín (quotiens).
Los números racionales incluyen a los números enteros (como -3, 0, 5) y son parte de los números reales.
Cuando escribimos un número racional en forma decimal, siempre obtenemos un número decimal que termina (finito) o un número decimal periódico (con cifras que se repiten sin fin). Por ejemplo, 1/2 es 0.5 (finito) y 1/3 es 0.333... (periódico).
Si un número real no es racional, se le llama número irracional. Los números irracionales tienen una parte decimal infinita que nunca se repite.
Contenido
Historia de los números racionales
¿Quiénes usaron las fracciones primero?
Los egipcios fueron de los primeros en usar fracciones para resolver problemas de la vida diaria. Ellos usaban fracciones donde el numerador era 1, como 1/2 o 1/3, para representar partes de un todo.
La idea de "conmensurable" en Grecia
Los matemáticos de la antigua Grecia, especialmente los pitagóricos, pensaban que todas las cantidades podían medirse con una unidad común. A esto lo llamaban "conmensurable". Creían que cualquier número podía ser una fracción de dos números enteros, es decir, un número racional.
El origen del nombre y el símbolo
La palabra "racional" viene del latín ratio, que significa "razón" o "cociente". Los matemáticos griegos usaban la palabra "logos" para referirse a estos números. El símbolo 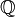para los números racionales fue propuesto por Giuseppe Peano en 1895, y viene de la palabra italiana quoziente (cociente).
Operaciones con números racionales
Los números racionales se pueden sumar, restar, multiplicar y dividir, igual que los números enteros.
Comparar números racionales
Para saber si una fracción es mayor, menor o igual que otra, podemos usar una regla sencilla:
- Si tenemos
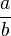y 
(con y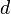 
positivos):
* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{a}{b} < \frac{c}{d} si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ad < bc * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{a}{b} > \frac{c}{d} si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ad > bc * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{a}{b} = \frac{c}{d} si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ad = bc
- Ejemplo: Compara Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{12}{4} y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{27}{3}
* Multiplicamos cruzado: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 12 \cdot 3 = 36 y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 4 \cdot 27 = 108 . * Como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 36 < 108 , entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{12}{4} < \frac{27}{3} .
- Si alguna fracción tiene un denominador negativo, primero la convertimos a una fracción equivalente con denominador positivo. Por ejemplo:
* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{a}{-b} = \frac{-a}{b} * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{-a}{-b} = \frac{a}{b}
Suma de números racionales
Para sumar dos fracciones, necesitamos que tengan el mismo denominador. Si no lo tienen, buscamos un denominador común:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{a}{b} + \frac{c}{d} = \frac{ad + bc}{bd}
Resta de números racionales
Restar es como sumar el número opuesto:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{a}{b} - \frac{c}{d} = \frac{ad - bc}{bd}
Multiplicación de números racionales
Para multiplicar fracciones, multiplicamos los numeradores entre sí y los denominadores entre sí:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d}
División de números racionales
Para dividir fracciones, multiplicamos la primera fracción por el inverso de la segunda:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} = \frac{a \cdot d}{b \cdot c} (recuerda que
no puede ser cero).
Inversos
- Inverso aditivo (opuesto): El inverso aditivo de 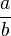es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): -\frac{a}{b} . Al sumarlos, el resultado es cero: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{a}{b} + (-\frac{a}{b}) = 0 .
- Inverso multiplicativo (recíproco): Si no es cero, el inverso multiplicativo de 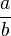es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{b}{a} . Al multiplicarlos, el resultado es uno: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{a}{b} \cdot \frac{b}{a} = 1 .
Cómo se escriben los números racionales en decimal
Todo número racional se puede escribir como un número decimal. Este decimal puede ser de tres tipos:
- Exacto: La parte decimal tiene un número limitado de cifras.
* Ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{8}{5} = 1,6
- Periódico puro: Toda la parte decimal se repite sin fin.
* Ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1}{7} = 0,142857142857\dots = 0,\overline{142857}
- Periódico mixto: Una parte de la sección decimal no se repite, y luego otra parte sí lo hace.
* Ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1}{60} = 0,01666\dots = 0,01\overline{6}
Si un número decimal es infinito y no es periódico, entonces no es un número racional. Por ejemplo, números como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 0,101001000100001\dots (donde se añade un cero más entre los unos cada vez) no son racionales. Los números como 
(pi) o 
son ejemplos de números irracionales, y por eso su parte decimal es infinita y no periódica.
Propiedades de los números racionales
Propiedades algebraicas
El conjunto de los números racionales 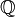tiene propiedades importantes con la suma y la multiplicación:
- Conmutativa: El orden de los números no cambia el resultado.
* Suma: 
* Multiplicación: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{a}{b}\times\frac{c}{d} = \frac{c}{d}\times\frac{a}{b}
- Asociativa: La forma en que agrupamos los números no cambia el resultado.
* Suma: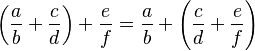 
* Multiplicación: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \left( \frac{a}{b}\times\frac{c}{d}\right ) \times\frac{e}{f} =\frac{a}{b}\times\left ( \frac{c}{d} \times\frac{e}{f} \right )
- Distributiva: La multiplicación se distribuye sobre la suma.
* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{a}{b} \times \left ( \frac{c}{d} +\frac{e}{f} \right )= \frac{a}{b} \times \frac{c}{d} + \frac{a}{b} \times \frac{e}{f}
- Elemento neutro:
* Para la suma, es el cero (0): Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{a}{b}+0= \frac{a}{b} . * Para la multiplicación, es el uno (1): Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{a}{b}\times 1 = \frac{a}{b} .
- Elemento simétrico (inverso):
* Para la suma, es el opuesto: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{a}{b}+ (-\frac{a}{b})= 0 . * Para la multiplicación, es el inverso multiplicativo (si el número no es cero): Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): q\times q^{-1} = 1 .
Propiedades de conjunto
El conjunto de los números racionales es "numerable". Esto significa que, aunque hay infinitos números racionales, podemos contarlos o ponerlos en una lista, uno por uno, si tuviéramos tiempo infinito. En cambio, los números reales (que incluyen a los irracionales) no son numerables; hay "más" números reales que racionales.
Propiedades de densidad
Los números racionales están "densamente" distribuidos en la recta numérica. Esto significa que entre dos números racionales cualesquiera, siempre puedes encontrar otro número racional. ¡Y entre esos dos, otro más, y así infinitamente! Esto hace que los racionales estén muy "juntos" en la recta numérica.
Véase también
En inglés: Rational number Facts for Kids
|
