Felix Klein para niños
Datos para niños Felix Klein |
||
|---|---|---|
 Felix Christian Klein, en imagen sin fecha.
|
||
| Información personal | ||
| Nombre de nacimiento | Felix Christian Klein | |
| Nacimiento | 25 de abril de 1849 Düsseldorf (Provincia del Rin, Reino de Prusia) |
|
| Fallecimiento | 22 de junio de 1925 Gotinga (Estado Libre de Prusia, República de Weimar) |
|
| Sepultura | Cementerio municipal de Gotinga y Gotinga | |
| Nacionalidad | Alemana (1871-1918, desde 1918) | |
| Familia | ||
| Cónyuge | Anna Klein | |
| Educación | ||
| Educado en | ||
| Supervisor doctoral | Julius Plücker y Rudolf Lipschitz | |
| Información profesional | ||
| Ocupación | Matemático, historiador de la matemática, profesor universitario, político y editor (desde 1872) | |
| Área | Geometría diferencial, teoría de grupos, geometría, matemáticas, function theory, educación y ecuación algebraica | |
| Cargos ocupados | Miembro de la Cámara de los Señores de Prusia (1908-1918) | |
| Empleador |
|
|
| Estudiantes doctorales | Carl Ferdinand von Lindemann, Carl Gustav Axel Harnack, Ludwig Bieberbach, Adolf Hurwitz, Grace Chisholm Young, Maxime Bôcher, Max Brückner, Friedrich Engel, Erwin Finlay-Freundlich, Robert Fricke, Edward Kasner, Alexander Ostrowski, Julio Rey Pastor, Victor Schlegel, Walther von Dyck y Karl Rohn | |
| Estudiantes | Walther von Dyck | |
| Obras notables |
|
|
| Conflictos | Guerra franco-prusiana | |
| Miembro de |
|
|
| Distinciones |
|
|
Felix Christian Klein (nacido en Düsseldorf el 25 de abril de 1849 y fallecido en Gotinga el 22 de junio de 1925) fue un matemático alemán muy importante. Él demostró que diferentes tipos de geometría, como la geometría euclidiana (la que aprendemos en la escuela) o las no euclidianas, son casos especiales de la geometría proyectiva.
En 1871, Klein presentó una forma innovadora de clasificar la geometría, conocida como el "programa de Erlangen". Este programa ayudó a unir diferentes ramas de la geometría. En su clasificación, el concepto de grupo (un conjunto de transformaciones que mantienen ciertas propiedades) es clave. Cada geometría se estudia a través del grupo de transformaciones que la define.
Al igual que otro matemático, Bernhard Riemann, Klein veía las funciones complejas como algo geométrico y aplicó estas ideas a la física. Sus estudios sobre las funciones modulares siguen siendo muy útiles para los investigadores de hoy.
Felix Klein fue profesor en la Universidad de Gotinga desde 1886. Fundó la Gran enciclopedia de las matemáticas en 1895. También fue un gran defensor de mejorar la enseñanza de las matemáticas en las escuelas secundarias. Klein era un excelente organizador de equipos científicos y de enseñanza. Gracias a él, Gotinga se convirtió en un centro muy importante para el desarrollo de las matemáticas en Europa.
Una superficie muy curiosa, la botella de Klein, lleva su nombre. Es una forma que tiene una sola cara.
Contenido
La vida académica de Felix Klein
Klein comenzó sus estudios en la Universidad de Bonn, donde fue alumno de Rudolf Lipschitz y Julius Plücker. Más tarde, trabajó como asistente de Plücker. Cuando Plücker falleció, Alfred Clebsch se encargó de terminar su trabajo, y Klein, que era muy talentoso, le ayudó mucho. En 1868, Klein obtuvo su doctorado con un trabajo sobre geometría aplicada a la mecánica.

En 1869, Klein estuvo en la Universidad de Berlín. Allí asistió a clases de Leopold Kronecker y participó en seminarios con Ernst Kummer y Karl Weierstrass. Fue en Berlín donde conoció a Sophus Lie, con quien se hizo amigo. En 1870, viajó a París con Lie para seguir estudiando. Sin embargo, tuvo que regresar a Alemania debido a un conflicto.
En 1871, Klein obtuvo el permiso para enseñar como profesor en Gotinga, gracias a la ayuda de Clebsch. Permaneció allí como profesor particular entre 1871 y 1872.
En 1872, Clebsch le ayudó a conseguir un puesto como profesor en Erlangen. Su carrera lo llevó en 1875 a la Universidad Técnica de Múnich. Ese mismo año, se casó con Anna Hegel, quien era nieta del famoso filósofo Georg Wilhelm Friedrich Hegel.
En 1880, Klein fue invitado a ser profesor de geometría en la Universidad de Leipzig. Esta etapa en Leipzig fue la más productiva de su carrera científica. Mantuvo correspondencia con Henri Poincaré y, al mismo tiempo, organizaba la enseñanza. Esta doble carga de trabajo le causó un gran agotamiento.
En 1886, aceptó un puesto en Gotinga, donde trabajó hasta su fallecimiento. Allí se dedicó intensamente a organizar la ciencia. Gracias a su gestión, David Hilbert fue invitado a Gotinga en 1895, lo que ayudó a que la ciudad se convirtiera en un centro mundial de las matemáticas. En 1914, Klein recibió el Premio Ackermann Teubner. Desde 1908, representó a la Universidad de Gotinga en el Parlamento de Prusia. En 1924, fue nombrado miembro honorario de la Sociedad Matemática Alemana (DMV), de la cual había sido presidente en 1897, 1903 y 1908.
Felix Klein falleció en Gotinga en 1925 y fue enterrado en el Cementerio de la ciudad.
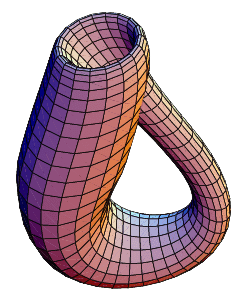
Las contribuciones de Felix Klein a las matemáticas
La tesis doctoral de Klein trataba sobre geometría lineal y cómo se aplica a la mecánica. En ella, clasificó ciertos tipos de complejos lineales usando la teoría de Karl Weierstrass.
Los primeros descubrimientos importantes de Klein en matemáticas ocurrieron en 1870. Junto con Sophus Lie, descubrió propiedades clave de las líneas asintóticas en la superficie de Kummer. Más tarde, estudiaron las curvas W, que son curvas que no cambian bajo ciertas transformaciones geométricas. Fue Lie quien le enseñó a Klein el concepto de grupo, que fue fundamental en sus trabajos posteriores. Klein también aprendió sobre grupos de Camille Jordan.
Klein ideó la "botella de Klein", una superficie cerrada que solo tiene un lado. No se puede dibujar en un espacio tridimensional sin que se cruce a sí misma, pero sí en un espacio de cuatro o más dimensiones. La botella de Klein se pensó como una banda de Möbius en tres dimensiones. Se puede construir uniendo los bordes de dos bandas de Möbius.
En la década de 1890, Klein se interesó más por la física matemática. Escribió sobre el giroscopio con Arnold Sommerfeld. En 1894, tuvo la idea de crear una enciclopedia de matemáticas que incluyera sus aplicaciones. Esta enciclopedia, llamada Encyklopädie der mathematischen Wissenschaften, se publicó hasta 1935 y se convirtió en una referencia muy importante.
El Programa de Erlangen: Una nueva visión de la geometría
En 1871, mientras estaba en Gotinga, Klein hizo descubrimientos muy importantes en geometría. Publicó dos artículos donde mostró que las geometrías euclidiana y no euclidiana podían verse como espacios métricos definidos por una métrica de Cayley-Klein. Esto significaba que la geometría no euclidiana era tan válida como la geometría euclidiana, poniendo fin a las discusiones sobre ella.
La forma en que Klein unió la geometría como el estudio de las propiedades de un espacio que no cambian bajo un grupo de transformaciones se conoce como el programa de Erlangen (1872). Este programa tuvo una gran influencia en cómo se desarrollaron las matemáticas. Klein presentó esta idea en su primera conferencia como profesor en Erlangen. El programa propuso un sistema unificado de geometría que hoy es el método aceptado. Klein demostró cómo las propiedades esenciales de una geometría se podían representar por el grupo de transformaciones que las conservan. Así, su definición de geometría incluía tanto la geometría euclidiana como la no euclidiana.
Hoy en día, la importancia de las ideas de Klein en geometría es muy clara. Se han integrado tanto en el pensamiento matemático que es difícil imaginar lo novedosas que fueron cuando se presentaron por primera vez.
El análisis complejo y las funciones
Klein consideraba su trabajo sobre análisis complejo como su mayor aporte a las matemáticas. Esto incluye su trabajo en:
- La conexión entre las ideas de Riemann y la teoría de invariantes.
- La teoría de números y el álgebra abstracta.
- La teoría de grupos.
- La geometría en más de 3 dimensiones y las ecuaciones diferenciales, especialmente las que él inventó y que son satisfechas por funciones modulares elípticas y funciones automórficas.
Klein demostró que el grupo modular mueve una región fundamental del plano complejo para cubrir todo el plano. En 1879, estudió la acción de un grupo matemático específico y obtuvo una representación de una superficie de Riemann que ahora se llama Cuártica de Klein. Demostró que era una curva compleja en el espacio proyectivo, y que su ecuación era x3y + y3z + z3x = 0. También mostró que su grupo de simetrías tenía un orden de 168. Su libro de 1882, Ueber Riemann's Theorie der algebraischen Funktionen und ihre Integrale, trata el análisis complejo de forma geométrica, uniendo la teoría del potencial y los mapeos conformes. Este trabajo se basó en ideas de la dinámica de fluidos.
Klein estudió ecuaciones de grado superior a 4 y le interesaba usar métodos especiales para resolver la ecuación general de quinto grado. Basándose en los métodos de Charles Hermite y Leopold Kronecker, obtuvo resultados similares a los de otros matemáticos y luego resolvió completamente el problema usando el grupo icosaédrico. Este trabajo le permitió escribir varios artículos sobre funciones modulares elípticas.
En su libro de 1884 sobre el icosaedro, Klein desarrolló una teoría de las funciones automórficas, conectando el álgebra y la geometría. Henri Poincaré había publicado un resumen de su teoría de las funciones automórficas en 1881, lo que llevó a una competencia amistosa entre los dos. Ambos intentaron formular y demostrar un gran teorema de uniformización que estableciera la nueva teoría de forma más completa. Klein logró formular dicho teorema y describir una estrategia para demostrarlo. Se le ocurrió su demostración durante un ataque de asma a las 2:30 de la madrugada del 23 de marzo de 1882.
Klein resumió su trabajo sobre funciones automórficas y funciones modulares elípticas en un tratado de cuatro volúmenes, escrito con Robert Fricke a lo largo de unos 20 años.
Gotinga: Un centro mundial de las matemáticas
El nombramiento de Klein en la Universidad de Gotinga fue impulsado por el director ministerial Friedrich Althoff. En los años siguientes, Althoff y Klein trabajaron juntos para convertir la Universidad de Gotinga en el centro matemático más importante del mundo. Esto duró hasta que muchos matemáticos alemanes fueron expulsados. Además de matemáticos importantes como David Hilbert, Richard Courant, Hermann Minkowski, Hermann Weyl y Emmy Noether, también llegaron a la universidad físicos destacados como Walther Nernst, Max Born, James Franck y Peter Debye. Las facultades de Matemáticas y Física de Gotinga se convirtieron en un modelo para muchas instituciones de investigación internacionales.
En 1893, Klein viajó por primera vez a los Estados Unidos de América. Este viaje y otros posteriores le dieron una gran influencia entre los matemáticos estadounidenses, muchos de los cuales fueron a estudiar a Gotinga. En Estados Unidos, se inspiró para orientar las matemáticas de la universidad más hacia la aplicación práctica. Klein implementó en Gotinga lo que había visto en Estados Unidos. Buscó contacto con ingenieros y encontró socios en Carl von Linde y Henry Theodore Böttinger, quienes le conectaron con la industria. Esto permitió crear un departamento de física técnica con financiación de la industria. En 1898, se fundó la Göttinger Vereinigung zur Förderung der angewandten Physik, la primera organización en Alemania que unía la industria y la universidad. Otras actividades en los años siguientes llevaron a la fundación de más institutos en Gotinga dedicados a la aplicación de la física o las matemáticas.
Otros científicos importantes llegaron a Gotinga, como el experto en hidrodinámica Ludwig Prandtl y el matemático aplicado Carl Runge.
Existía un contraste entre las escuelas de matemáticos de Berlín (como Karl Weierstrass, Leopold Kronecker, Ernst Eduard Kummer), que ponían énfasis en el rigor matemático, y la escuela de Felix Klein (y sus maestros, Alfred Clebsch y Julius Plücker), que prefería las investigaciones geométricas y físicas. Esto es importante para entender el papel de Klein en las matemáticas alemanas de finales del siglo XIX. Esta diferencia llegó a ser una hostilidad abierta en ocasiones. El contraste entre los matemáticos de Berlín y Gotinga como escuelas dominantes en Alemania continuó en la primera mitad del siglo XX.
Reconocimientos y honores
Felix Klein fue elegido miembro extranjero de la Royal Society el 10 de diciembre de 1885.
La Sociedad Matemática de Londres le otorgó la Medalla De Morgan en 1893.
En 1908, durante el Congreso Internacional de Matemáticos en Roma, Klein fue elegido presidente de la Comisión Internacional de Instrucción Matemática (ICMI).
Recibió la Medalla Copley en 1912.
Un asteroide del cinturón principal, descubierto el 30 de marzo de 1997, lleva su nombre: (12045) Klein.
El legado de Felix Klein
En 2008, la Unión Matemática Internacional y la Comisión Internacional de Educación Matemática lanzaron el “Proyecto Klein”. Este proyecto busca publicar una obra general sobre matemáticas, que era una ambición de Klein. El proyecto publicó su libro Matemáticas elementales desde un punto de vista superior, cuyo primer volumen trata sobre aritmética, álgebra y análisis, y el segundo sobre geometría. Un tercer y último volumen, Matemáticas de precisión y aproximación, se publicó en 1928, después de su muerte. Este texto tuvo un gran impacto en Alemania y en toda Europa.
Felix Klein era una persona trabajadora, organizada y sistemática. Una de las colecciones más impresionantes de Gotinga es la de los Protocolos de Seminario de Felix Klein. Es un registro detallado de más de 8.000 páginas manuscritas, reunidas en 29 volúmenes. Contiene cuarenta años de seminarios, conferencias y cursos impartidos por Klein, sus colegas, sus estudiantes y visitantes. Los Protocolos comenzaron en 1872 y continuaron hasta su jubilación en 1913. Ahora se pueden ver digitalmente gracias a un proyecto del Instituto Clay de Matemáticas.
El proyecto editorial más ambicioso de Felix Klein fue la edición de una enciclopedia sobre matemáticas y sus aplicaciones (Encyclopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen). La inclusión de aplicaciones se debe a su convicción de que son esenciales para entender mejor las matemáticas. El primer volumen apareció en 1898 y el último en 1933. En total, fueron seis volúmenes, distribuidos en unos treinta libros, que suman más de 20.000 páginas. El jefe del proyecto fue Walther von Dyck, pero Klein participó activamente en la creación del plan general, por lo que la obra a veces se llama "Enciclopedia de Klein".
Galería de imágenes
-
Esquema de una botella de Klein
Véase también
 En inglés: Felix Klein Facts for Kids
En inglés: Felix Klein Facts for Kids
- Botella de Klein
- j-invariante
- Cuártica de Klein
- Grupo de Klein
- Enciclopedia de Klein
- Homomorfismo