Operación (matemática) para niños

Enciclopedia para niños

Una operación matemática es como una regla o un proceso que toma uno o más números (o elementos) y los transforma en un único resultado. Imagina que tienes una máquina: le metes unos ingredientes (los números) y, siguiendo unas instrucciones, la máquina te da un producto final.

Para que algo sea una operación matemática, debe cumplir dos cosas importantes:

Siempre debe dar un resultado. No puede haber casos en los que la operación "no sepa qué hacer".
Siempre debe dar un único resultado. Si metes los mismos números, el resultado siempre será el mismo.

La cantidad de números que necesita una operación se llama aridad. Por ejemplo, la suma o la multiplicación necesitan dos números, por eso se llaman operaciones binarias.

En el álgebra y la aritmética, usamos operaciones como la suma, la resta, la multiplicación y la división. Estas operaciones toman números de un conjunto (por ejemplo, los números enteros) y los relacionan para obtener otro número.

Contenido

Propiedades de las operaciones básicas
Tipos de operaciones según la cantidad de elementos
Galería de imágenes
Véase también

Propiedades de las operaciones básicas

Las operaciones matemáticas tienen propiedades que nos ayudan a entender cómo funcionan.

La suma (+)

Se escribe como $\, a + b$ .
Es conmutativa: El orden de los números no cambia el resultado. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, 2 + 3 = 5 y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, 3 + 2 = 5 . Esto se escribe como $\, a + b = b + a$ .
Es asociativa: Si sumas tres o más números, no importa cómo los agrupes. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, (2 + 3) + 4 = 5 + 4 = 9 y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, 2 + (3 + 4) = 2 + 7 = 9 . Esto se escribe como $\, (a + b) + c = a +(b + c)$ .
Tiene una operación inversa llamada sustracción (resta): Si sumas un número y luego lo restas, vuelves al inicio. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, (5 + 3) - 3 = 5 .
Tiene un elemento neutro que es el 0: Sumar 0 a cualquier número no lo cambia. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, 7 + 0 = 7 . Esto se escribe como $\, a + 0 = a$ .

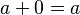La multiplicación (×)

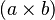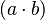Se escribe como $\, (a \times b)$ o $\,( a \cdot b )$ .
Es una suma repetida: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a \times n significa sumar 'a' 'n' veces.
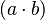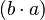Es conmutativa: El orden de los números no cambia el resultado. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, 2 \times 3 = 6 y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, 3 \times 2 = 6 . Esto se escribe como $\, (a \cdot b )$ = $\, (b \cdot a)$ .
Es asociativa: Si multiplicas tres o más números, no importa cómo los agrupes. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, (2 \times 3) \times 4 = 6 \times 4 = 24 y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, 2 \times (3 \times 4) = 2 \times 12 = 24 . Esto se escribe como $\, (a \cdot b) \cdot c = a \cdot (b \cdot c)$ .
Tiene una operación inversa llamada división (para números que no son cero): Si multiplicas un número y luego lo divides por el mismo número, vuelves al inicio. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{(5 \times 3)}{3} = 5 .
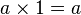Tiene un elemento neutro que es el 1: Multiplicar por 1 no cambia el número. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 7 \times 1 = 7 . Esto se escribe como $a \times 1 = a$ .
Es distributiva respecto a la suma: Puedes multiplicar un número por una suma, o multiplicar el número por cada parte de la suma y luego sumar los resultados. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, (2 + 3) \cdot 4 = 5 \cdot 4 = 20 y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, (2 \cdot 4) + (3 \cdot 4) = 8 + 12 = 20 . 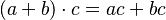Esto se escribe como $\, (a + b) \cdot c = ac + bc$ .

La potenciación

Se escribe como $\, a^{b}$ .
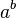Es una multiplicación repetida: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a^{n} significa multiplicar 'a' por sí mismo 'n' veces. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2^3 = 2 \times 2 \times 2 = 8 .
No es conmutativa ni asociativa: El orden o la agrupación sí importan. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, 2^{3} = 8 pero Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, 3^{2} = 9 .
Tiene operaciones inversas llamadas logaritmación y radicación (raíces).
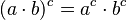Es distributiva con respecto a la multiplicación: $\, (a \cdot b)^{c} = a^{c} \cdot b^{c}$ .
Tiene propiedades como: 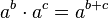$\ {a^{b}} \cdot {a^{c}} = a^{b + c}$ (cuando multiplicas potencias con la misma base, sumas los exponentes).
Y también: 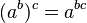$\, (a^{b})^{c} = a^{bc}$ (cuando elevas una potencia a otra potencia, multiplicas los exponentes).

Orden de las operaciones

Cuando tienes una expresión con varias operaciones, es muy importante saber en qué orden resolverlas. Esto se conoce como el orden de prioridad o precedencia de las operaciones. Una forma común de recordarlo es con el acrónimo PEMDAS (Paréntesis, Exponentes, Multiplicación y División, Adición y Sustracción).

1. Primero, resuelve las operaciones dentro de los paréntesis (o corchetes, llaves). 2. Luego, calcula las exponentes (potencias y raíces). 3. Después, haz las multiplicaciones y divisiones de izquierda a derecha. 4. Finalmente, realiza las sumas y restas de izquierda a derecha.

Propiedades de la igualdad

La relación de igualdad (=) significa que dos cosas tienen el mismo valor. Tiene estas propiedades:

Reflexiva: Cualquier cosa es igual a sí misma. $\, a = a$ .
Simétrica: Si 'a' es igual a 'b', entonces 'b' es igual a 'a'. Si $\, a = b$ entonces $\, b = a$ .
Transitiva: Si 'a' es igual a 'b', y 'b' es igual a 'c', entonces 'a' es igual a 'c'. Si $\, a = b$ y $\, b = c$ entonces $\, a = c$ .

Leyes de la igualdad

Estas son reglas que se cumplen con la igualdad:

Si sumas o multiplicas la misma cantidad a ambos lados de una igualdad, la igualdad se mantiene. Si $\, a = b$ entonces $\, a + c = b + c$ .
Si dos símbolos son iguales, puedes reemplazar uno por el otro en cualquier expresión.
Si $\, a + c = b + c$ , entonces $\, a = b$ .
Si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, a \cdot c = b \cdot c y 'c' no es cero, entonces $\, a = b$ .

Leyes de la desigualdad

La relación de desigualdad (<, >, ≤, ≥) significa que un valor es mayor o menor que otro.

Transitiva: Si 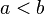$\, a < b$ y $\, b < c$ , entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, a < c .
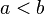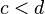Si sumas la misma cantidad a ambos lados de una desigualdad, la desigualdad se mantiene. Si $\, a < b$ y $\, c < d$ entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, a + c < b + d .
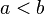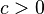Si multiplicas ambos lados de una desigualdad por un número positivo, la desigualdad se mantiene. Si $\, a < b$ y $\, c > 0$ entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, ac < bc .
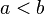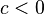Si multiplicas ambos lados de una desigualdad por un número negativo, la dirección de la desigualdad cambia. Si $\, a < b$ y $\, c < 0$ entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, bc < ac .

Regla de los signos

Cuando multiplicas o divides números positivos (+) y negativos (-), se siguen estas reglas:

$\begin{cases} + \cdot - = - \\ + \cdot + = + \\ - \cdot - = + \\ - \cdot + = - \\ \end{cases}$

En resumen:

Signos iguales (ambos positivos o ambos negativos) dan resultado positivo.
Signos diferentes (uno positivo y uno negativo) dan resultado negativo.

Tipos de operaciones según la cantidad de elementos

Las operaciones se pueden clasificar según cuántos elementos necesitan para funcionar.

Operación binaria

Una operación es binaria cuando necesita dos elementos para dar un resultado. La suma y la multiplicación son ejemplos de operaciones binarias. Por ejemplo, en los números naturales, la suma 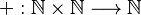$+: \mathbb{N} \times \mathbb{N} \longrightarrow \mathbb{N}$ toma dos números naturales (como 3 y 5) y da como resultado otro número natural (8).

Operación unaria

Una operación unaria necesita solo un elemento para dar un resultado. A menudo se les llama funciones. Un ejemplo es la operación de "incremento" o "siguiente" en los números naturales, donde a un número le sumas 1. Si tienes el número 5, la operación de incremento te da 6. Otro ejemplo es la operación "opuesto" en los números enteros. Si tienes el número 7, su opuesto es -7.

Operación 0-aria

Una operación 0-aria no necesita ningún elemento de entrada. Simplemente devuelve un valor fijo, como una constante. Un ejemplo es la operación que devuelve el valor de pi (aproximadamente 3.14159...). No necesitas darle ningún número para que te dé pi.

Operación externa

A veces, una operación combina elementos de dos conjuntos diferentes para producir un resultado que pertenece a uno de esos conjuntos (o a un tercero). Un ejemplo es la multiplicación de un número real por un vector. Si tienes un vector (que tiene dirección y magnitud) y lo multiplicas por un número, obtienes un nuevo vector. Por ejemplo, si multiplicas el vector (3,6) por el número 3, obtienes el vector (9,18). El número y el vector son de tipos diferentes, pero el resultado es un vector.

Otro ejemplo es el Producto escalar de dos vectores. Aquí, tomas dos vectores y el resultado es un número real. Por ejemplo, si multiplicas los vectores (3,6) y (5,2), el resultado es el número 27.

Galería de imágenes

Una operación binaria toma dos elementos (a y b) y los combina para producir un resultado (c).

Véase también

En inglés: Operation (mathematics) Facts for Kids

Relación matemática
Correspondencia matemática
Función matemática
Propiedades de las operaciones binarias

Obtenido de «https://ninos.kiddle.co/index.php?title=Operación_(matemática)&oldid=4909917»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Operación (matemática) para Niños. Enciclopedia Kiddle.