Mecánica clásica para niños

La mecánica clásica es una parte de la física que estudia cómo se mueven los objetos grandes, como pelotas, coches o planetas, y cómo las fuerzas afectan ese movimiento. Se enfoca en objetos que no son extremadamente pequeños (como los átomos) y que no se mueven a velocidades cercanas a la de la velocidad de la luz.

Esta rama de la física nos ayuda a entender por qué las cosas se mueven, se detienen o cambian de dirección. Es la base de muchas cosas que vemos y usamos todos los días.

Esta sección es un extracto de Anexo:Cronología de la mecánica clásica § Cronología de la mecánica clásica.

En la tabla que sigue solamente en la primera aparición de un autor se recoge el nombre completo y las fechas de nacimiento y fallecimiento; en las siguientes, solamente el enlace con el apellido.

Cronología de la mecánica clásica

Año	País	Autor	Acontecimiento	Época
ca. siglo IV a. C.		Aristóteles (384-322 a. C.)	Aristóteles concibe el sistema de la física aristotélica, que luego es ampliamente refutado.	Mecánica temprana
siglo IV a. C.			astrónomos babilónicos calculan la posición de Júpiter utilizando el teorema de la velocidad media.
260 a. C.		Arquímedes	Demuestra matemáticamente el principio de la palanca y descubrió el principio que lleva su nombre y que relaciona el peso con la flotabilidad.
60 a. C.		Herón de Alejandría (c. 10-70 d. C.)	Escribe Metrica, Mechanics (sobre levantar objetos pesados) y Pneumatics (sobre máquinas que trabajan a presión).
350		Temistio (ca. 317-ca. 388)	Afirma que la fricción estática es mayor que la fricción cinética.
1.ª mitad del siglo XIX		Juan Filópono (490-566)	Introduce los conceptos de "ímpetu" (el moderno momento) y "fuerza motriz". Según su teoría, la acción inicial realizada sobre la piedra le comunica un ímpetu, y era ese ímpetu el que sostenía el movimiento. El ímpetu perdía gradualmente su fuerza debido a la penetración de la piedra en el medio aéreo, y una vez que ese impulso se agotaba, la piedra asumía su movimiento natural y caía. Los proyectiles continuaban avanzando por el efecto de una fuerza impulsora transmitida por el lanzador (y no por el empuje del aire). El aire era un obstáculo para el movimiento de los proyectiles. El vacío existía y el movimiento en el vacío era posible. También señala que por observación, dos bolas de pesos muy diferentes caerán casi a la misma velocidad, una prueba del principio de equivalencia.
1000-1030		Abū Rayhān al-Bīrūnī (973-1050)	Introduce el método científico experimental en la estática y en la dinámica, y las unifica en la ciencia de la mecánica; también combina los dominios de la hidrostática con la dinámica de crear el campo de la hidrodinámica, que él ayudó a matematizar.
1000-1030		Alhazen (965-1040) y Avicena (980-1037)	Desarrollan los conceptos de inercia y de la cantidad de movimiento.
1021		Al-Biruni	Usa tres coordenadas ortogonales para describir un punto en el espacio.
1100-1138		Avempace (c.1085-1138)	Desarrolla el concepto de fatiga, que según Shlomo Pines es precursor de la idea leibniziana de fuerza de reacción.
1100-1165		Hibat Allah Abu'l-Barakat al-Baghdaadi (c. 1080-1165)	Descubre que la fuerza es proporcional a la aceleración en lugar de a la velocidad, ley fundamental en la mecánica clásica.
1121		Al-Jazini (c. 1077-1155)	Publica The Book of the Balance of Wisdom, en la que se desarrolla los conceptos de energía potencial gravitatoria y de gravedad remota
1340-1358		Jean Buridan (c. 1300 - c. 1358)	Desarrolla la teoría del ímpetu.
1490		Leonardo da Vinci	Describe la capilaridad.
Siglo XIV			Los calculadores de Oxford y colaboradores franceses prueban el teorema de la velocidad media.
Siglo XIV		Nicole Oresme (c.1323-1382)	Deriva la ley del cuadrado de los tiempos para el cambio uniformemente acelerado. Oresme, sin embargo, consideró este descubrimiento como un ejercicio puramente intelectual que no tenía relevancia para la descripción de ningún fenómeno natural y, en consecuencia, no reconoció ninguna conexión con el movimiento de los cuerpos en aceleración.
Siglo XVI		Francesco Beato y Luca Ghini (1490-1566)	Experimentalmente, contradicen la visión aristotélica sobre la caída libre.
Siglo XVI		Domingo de Soto (1494-1560)	Sugiere que los cuerpos que caen a través de un medio homogéneo se aceleran uniformemente. Sin embargo, no anticipó muchas de las calificaciones y refinamientos contenidos en la teoría de la caída de los cuerpos de Galileo. Por ejemplo, no reconoció, como sí hizo Galileo, que un cuerpo caería con una aceleración estrictamente uniforme solo en el vacío, alcanzando, de otro modo, finalmente una velocidad terminal uniforme.
1500-1528		Al-Birjandi (?-1525/28)	Desarrolla la teoría de la «inercia circular» para explicar la rotación de la Tierra
1581		Galileo Galilei (1564-1642)	Destaca la propiedad del isócronismo del péndulo.
1589		Galileo	Utiliza bolas rodando por planos inclinados para mostrar que diferentes pesos caen con la misma aceleración.
1638		Galileo	Publica el Discorsi e dimostrazioni matematiche, intorno à due nuove scienze (que eran la ciencia de los materiales y la cinemática) donde desarrolla, entre otras cosas, la transformación galileana.
1644		René Descartes (1596-1650)	Sugiere una forma temprana de la ley de conservación del impulso.
1645		Ismaël Bullialdus (1605-1694)	Argumenta que la «gravedad» se debilita como el inverso del cuadrado de la distancia.
1651		Giovanni Battista Riccioli y Francesco Maria Grimaldi	Descubren el efecto Coriolis
1658		Christian Huygens (1629-1695)	Descubre experimentalmente que bolas colocadas en cualquier lugar en el interior de un cicloide invertido llegan al punto más bajo de este cicloide simultáneamente y, por tanto, muestra que la cicloide es la curva tautócrona (o isócrona).
1668		John Wallis (1616-1703)	Sugiere la ley de conservación de la cantidad de movimiento.
1673		Huygens	Publica su Horologium Oscillatorium. Huygens describe en este trabajo las dos primeras leyes del movimiento. El libro es también el primer tratado moderno en el que un problema físico (el movimiento acelerado de un cuerpo que cae) se idealiza mediante un conjunto de parámetros y luego se analiza matemáticamente.
1676-1689		Leibniz (1646-1716)	Desarrolla el concepto de vis viva, una teoría limitada de la conservación de energía.
1677		Baruch Spinoza (1632-1677)	Presenta una noción primitiva de la primera ley de Newton.
1687		Isaac Newton (1642/43-1727)	Publica sus Philosophiae Naturalis Principia Mathematica, en la que formula las leyes del movimiento de Newton y la ley de la gravitación universal.	Formación de la mecánica newtoniana
1690		Jakob Bernoulli (1654-1705)	Demuestra que el cicloide es la solución del problema tautócrono.
1691		Johann Bernoulli (1667-1748)	Muestra que una cadena libremente suspendida entre dos puntos formará una catenaria.
1691		Bernoulli, Jak.	Demuestra que la curva de la catenaria tiene el centro de gravedad más bajo que cualquier cadena que cuelgue entre dos puntos pueda tener.
1696		Bernoulli, Joh.	Demuestra que la cicloide es la solución del problema de la braquistócrona.
1707		Gottfried Leibniz (1646-1716)	Probablemente desarrolla el principio de mínima acción.
1710		Jakob Hermann (1678-1733)	muestra que el vector de Laplace-Runge-Lenz se conserva para un caso de fuerza central del cuadrado inversos.
1714		Brook Taylor (1685-1731)	Calcula la frecuencia fundamental de una cuerda vibrante estirada en función de su tensión y de su masa por unidad de longitud resolviendo una ecuación diferencial ordinaria.
1733		Daniel Bernoulli (1000-1782)	Calcula la frecuencia fundamental y los armónicos de una cadena colgante esolviendo una ecuación diferencial ordinaria.
1734		Bernoulli, D.	Resuelve una ecuación diferencial ordinaria para las vibraciones de una barra elástica empotrada en un extremo (viga en voladizo).
1738		Bernoulli, D.	Calcula el flujo de un fluido en hidrodinámica (teorema de Bernoulli).
1739		Leonhard Euler (1707-1783)	Resuelve la ecuación diferencial ordinaria de un oscilador armónico forzado y nota el fenómeno de la resonancia (mecánica).
1742		Colin Maclaurin (1698-1746)	Descubre su esferoide de Clairaute auto-gravitante en rotación uniforme.
1743		Jean le Rond d'Alembert (1717-1783)	Publica su Traite de Dynamique, en el que introduce el concepto de fuerzas generalizadas y el principio de d'Alembert.
1747		D'Alembert y Alexis Clairaut	Publican las primeras soluciones aproximadas al problema de los tres cuerpos.
1747		Pierre Louis Moreau de Maupertuis (1698-1759)	Aplica el principio de mínima acción a la mecánica.
1749		Euler	Deriva la ecuación para la aceleración de Coriolis
1759		Euler	Resuelve la ecuación en derivadas parciales de la vibración de un tambor rectangular.
1764		Euler	Estudia la ecuación en derivadas parciales de la vibración de un tambor circular y encuentra una de las soluciones (función de Bessel).
1776		John Smeaton (1724-1792)	Publica en un artículo con experimentos que vinculan la potencia, el trabajo, la cantidad de movimiento y la energía cinética, y apoya la teoría de la conservación de la energía.
1788		Joseph-Louis Lagrange (1736-1813)	Presenta las ecuaciones del movimiento de Lagrange en su libro Mécanique Analytique.
1789		Antoine Lavoisier (1743-1794)	Establece la ley de la conservación de la masa.
1803		Louis Poinsot (1777-1859)	Desarrolla la idea de la conservación del momento angular (este resultado se conocía anteriormente solo en el caso de la conservación de la velocidad areolar).
1813		Peter Ewart (1767-1842)	Sostiene la idea de la conservación de energía en su artículo On the measure of moving force.
1821		William Hamilton (1805-1865)	Comienza el análisis de la función característica de Hamilton y de la Ecuación de Hamilton-Jacobi.
1829		Carl Friedrich Gauss (1777-1855)	Introduce el principio de mínima restricción de Gauss
1834		Poinsot	observa un ejemplo del teorema del eje intermedio.
1834		Charles Jacobi (1804-1851)	Descubre sus elipsoides auto-gravitantes en rotación uniforme.
1834		John Russell (1808-1882)	Observa una onda solitaria persistente (soliton) en el Canal de la Unión cerca de Edimburgo y utiliza un recipiente lleno de agua para estudiar la dependencia de la velocidad de la ola solitaria a la amplitud de la onda y a la profundidad del agua.
1835		Hamilton	Establece las ecuaciones canónicas del movimiento de Hamilton.
1835		Gaspard Coriolis (1792-1843)	Analiza teóricamente el rendimiento mecánico de los molinos de agua y descubre la fuerza de Coriolis.
1838		Joseph Liouville (1809-1882)	Comienza a trabajar en el teorema de Liouville .
1.ª mitad del XIX		Augustin Louis Cauchy (1789-1857))	Desarrolla su ecuación de cantidad de movimiento y su tensor de tensión.
1841		Julius Robert von Mayer (1814-1878)	Meyer, científico aficionado, escribe un artículo sobre la conservación de energía, pero su falta de formación científica conduce a su rechazo.
1842		Christian Doppler (1803-1853)	Descubre el efecto Doppler
1847		Hermann von Helmholtz (1821-1894)	Establece formalmente la ley de conservación de la energía.
1851		Léon Foucault (1819-1868)	Prueba la rotación de la Tierra con un péndulo gigantesco (péndulo de Foucault).
1870		Rudolf Clausius (1822-1888)	Deduce el teorema del virial, quee relaciona la energía cinética total promedio de un sistema con su energía potencial promedio.
1902		James Jeans (1877-1946)	Calcula la longitud característica necesaria para que las perturbaciones gravitacionales crezcan en un medio estático casi homogéneo.
1915		Emmy Noether (1882-1935)	demuestra el teorema de Noether, del cual se deducen las leyes de conservación.
1952		Parker	Desarrolla una forma de tensor del teorema del virial.
1978		Vladimir Arnold (1937-2010)	Establece la forma precisa del `teorema de Liouville-Arnold.
1983		Mordehai Milgrom	Propone la dinámica newtoniana modificada
1992		Firdaus E. Udwadia y Robert E. Kalaba	Crean la ecuación Udwadia–Kalaba, un método para derivar las ecuaciones de movimiento de un sistema mecánico restringido.

¿Qué es la Mecánica Clásica?

La mecánica clásica es la parte de la física que estudia el movimiento de los cuerpos. Se aplica a objetos que podemos ver y tocar, y que se mueven a velocidades normales, no extremadamente rápidas. Nos ayuda a predecir dónde estará un objeto y cómo se moverá en el futuro.

En la mecánica clásica, se considera que el tiempo es igual para todos. Además, las leyes que rigen el movimiento son deterministas, lo que significa que si conocemos el estado actual de un objeto, podemos saber cómo se moverá después.

Historia de la Mecánica Clásica

El estudio del movimiento es muy antiguo. Desde la Antigua Grecia, filósofos como Aristóteles intentaron explicar cómo se movían las cosas.

Primeros Pasos y Observaciones

• En el siglo XI, científicos como al-Biruni y Alhazen en el mundo islámico hicieron importantes avances. Unificaron el estudio de los objetos en reposo (estática) y en movimiento (dinámica). También desarrollaron ideas sobre la inercia y la cantidad de movimiento.
• Galileo Galilei (1564-1642) fue clave. Realizó experimentos, como dejar caer objetos desde alturas, para entender cómo caen. Descubrió que los objetos caen con la misma aceleración sin importar su peso, si no hay resistencia del aire. Sus ideas sobre el movimiento acelerado son fundamentales.
• Johannes Kepler (1571-1630) estudió el movimiento de los planetas. Descubrió que los planetas se mueven en elipses alrededor del Sol, no en círculos perfectos.

La Era de Isaac Newton

Sir Isaac Newton (1643-1727), una figura muy importante en la historia de la física.

Isaac Newton (1642-1727) fue una figura central. En 1687, publicó su libro Philosophiæ naturalis principia mathematica, donde presentó sus famosas tres leyes del movimiento y la ley de la gravitación universal.

Las leyes de Newton explican:

• Por qué un objeto en movimiento sigue moviéndose o uno en reposo se queda quieto, a menos que una fuerza actúe sobre él (Ley de la Inercia).
• Cómo una fuerza causa que un objeto acelere (Segunda Ley).
• Que por cada acción hay una reacción igual y opuesta (Tercera Ley).

Newton también explicó la gravedad, mostrando que estas leyes se aplican tanto a objetos en la Tierra como a los planetas en el espacio. Sus ideas fueron tan precisas que pudieron explicar las leyes de Kepler sobre el movimiento planetario.

Desarrollos Posteriores

Después de Newton, otros científicos como Joseph-Louis Lagrange y William Rowan Hamilton desarrollaron formas más avanzadas de la mecánica clásica. Estas nuevas formas, llamadas mecánica lagrangiana y mecánica hamiltoniana, usaban matemáticas más complejas para resolver problemas de movimiento de manera más general.

Ramas Principales de la Mecánica Clásica

La mecánica clásica se divide en varias áreas para estudiar diferentes aspectos del movimiento:

• Estática: Estudia los objetos que están en equilibrio, es decir, que no se mueven o se mueven a velocidad constante.
• Dinámica: Se enfoca en el movimiento de los objetos y cómo las fuerzas causan esos movimientos.
• Cinemática: Describe el movimiento de los objetos sin preocuparse por las fuerzas que lo causan. Por ejemplo, solo describe la velocidad y la posición.

También se puede dividir por el tipo de aplicación:

• Mecánica celeste: Estudia el movimiento de los planetas, estrellas y otros cuerpos en el espacio.
• Mecánica continua: Se ocupa de cómo se mueven los materiales que fluyen, como los líquidos y los gases, o los sólidos que se deforman.

¿Cómo se Estudia el Movimiento?

La mecánica clásica usa dos maneras principales para entender el movimiento:

Observación y Experimentación

Esta forma se basa en observar y medir lo que sucede en el mundo real. Por ejemplo, si dejas caer una pelota, puedes medir su velocidad en diferentes momentos. Al analizar esos datos, puedes encontrar una fórmula que describa cómo se mueve la pelota.

Razonamiento y Matemáticas

Aquí, se parte de ideas básicas y se usan las matemáticas para crear fórmulas y predecir el movimiento. Por ejemplo, si sabes que la aceleración de la gravedad es constante, puedes usar el cálculo infinitesimal para deducir la misma fórmula de la velocidad de la pelota que obtuviste con los experimentos.

Ambas formas se complementan. Los experimentos confirman las teorías matemáticas, y las teorías nos ayudan a entender mejor lo que observamos.

Límites de la Mecánica Clásica

Aunque la mecánica clásica es muy útil para la vida diaria, no puede explicar todo. Hay situaciones donde necesitamos otras teorías más avanzadas:

• Objetos muy pequeños: Cuando los objetos son tan diminutos como los átomos o las partículas, la mecánica clásica no funciona. Para esto, usamos la mecánica cuántica.
• Velocidades muy altas: Si los objetos se mueven a velocidades cercanas a la de la velocidad de la luz, la mecánica clásica no es precisa. En estos casos, se usa la teoría de la relatividad especial de Albert Einstein.
• Objetos muy masivos: Para objetos extremadamente grandes y pesados, como los agujero negros o la forma del universo, se necesita la relatividad general.

A pesar de estas limitaciones, la mecánica clásica sigue siendo fundamental. Es la base para entender el movimiento de cohetes, coches, pelotas y muchas otras cosas en nuestro mundo cotidiano.

Galería de imágenes

• 

  El sistema solar se puede explicar con gran aproximación mediante la mecánica clásica, usando las leyes de movimiento y gravitación universal de Newton.

• 

  Giróscopo, un dispositivo mecánico

• 

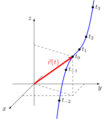
  Trayectoria de una partícula y su posición en función del tiempo

• 

  Espacio de fases de un péndulo forzado. El sistema se hace caótico

Véase también

En inglés: Classical mechanics Facts for Kids

• Relatividad especial de Einstein
• Mecánica cuántica
• Teoría cuántica de campos
• Mecánica puntual
• Mecánica de medios continuos