Teoría cuántica de campos para niños

La teoría cuántica de campos es una rama de la física que combina dos ideas muy importantes: la mecánica cuántica y la teoría de campos clásica. Imagina que la energía y la materia no solo existen como partículas pequeñas, sino también como "campos" que se extienden por todo el espacio, como el campo magnético. Esta teoría nos ayuda a entender cómo se comportan estos campos a nivel cuántico.

Una de las ideas más sorprendentes de la teoría cuántica de campos es que el comportamiento de un campo continuo (como la luz) es como si estuviera hecho de muchas partículas que pueden aparecer o desaparecer. Es decir, las partículas pueden crearse o destruirse. A esta teoría también se le conoce como TCC o QFT (por sus siglas en inglés).

Se usa mucho en la física de altas energías, que estudia las partículas subatómicas (las partes más pequeñas de la materia) y cómo interactúan. Gracias a ella, podemos entender fenómenos como la existencia de la antimateria.

También es una herramienta útil en la física de la materia condensada. Aquí, se usa para describir cómo se mueven y se organizan grandes grupos de partículas, ayudando a explicar cosas como la superconductividad (cuando algunos materiales conducen electricidad sin resistencia) o la superfluidez (cuando un líquido fluye sin fricción).

La teoría cuántica del campo electromagnético, llamada electrodinámica cuántica, fue la primera en desarrollarse y es la teoría física más precisa que se ha comprobado con experimentos. Grandes científicos como Paul Dirac, Richard Feynman y otros, sentaron las bases de esta teoría entre los años 1920 y 1950.

Dispersión de neutrones. Cuando los neutrones chocan con los átomos que vibran en un cristal, se dispersan. Esto se puede entender como la absorción o emisión de fonones (cuantos de las ondas sonoras del cristal) por el neutrón.

Partículas y campos, clásicos y cuánticos. Las ideas clásicas de partícula y campo comparadas con las cuánticas. Una partícula cuántica no tiene una posición fija, sino que su ubicación se describe con una probabilidad. Un campo cuántico es como un grupo de partículas cuánticas.

Historia de la teoría cuántica de campos

La teoría cuántica de campos se desarrolló al mismo tiempo que la mecánica cuántica "normal". Los científicos querían explicar los fenómenos atómicos, pero también necesitaban considerar las leyes de la relatividad especial.

Entre 1926 y 1928, Erwin Schrödinger y Paul Dirac intentaron crear ecuaciones que describieran el movimiento de una partícula cuántica de forma relativista. Sin embargo, estas ecuaciones tenían algunos problemas.

Por otro lado, en 1926, Werner Heisenberg, Pascual Jordan y Max Born estudiaron cómo se comportaba la luz (radiación electromagnética) dentro de un espacio cerrado. Este fue el primer ejemplo de una teoría cuántica de campos, donde la radiación se comportaba como un conjunto de partículas llamadas fotones, tal como había propuesto Albert Einstein en 1905.

Después de esto, las ecuaciones relativistas se vieron de otra manera. En lugar de ser solo "funciones de onda", se usaron reglas especiales para tratarlas como campos. Así, se obtuvieron ecuaciones para partículas cuánticas que sí eran consistentes con la relatividad. Este proceso se conoce como segunda cuantización y fue desarrollado por Heisenberg, Wolfgang Pauli y otros.

A pesar de sus éxitos, la teoría cuántica de campos tenía un problema: al calcular algunas cantidades físicas, los resultados daban "infinito", lo cual no tenía sentido. Este problema se resolvió entre los años 1930 y 1940 por científicos como Julian Schwinger, Richard Feynman y Shin'ichiro Tomonaga, usando una técnica llamada renormalización. Esto llevó al desarrollo de la moderna electrodinámica cuántica (QED). Los diagramas de Feynman, que son dibujos que ayudan a calcular interacciones, se convirtieron en una herramienta fundamental.

En los años 50, la QED se extendió a otras teorías llamadas teorías gauge. A finales de los 60, Sheldon Glashow, Abdus Salam y Steven Weinberg unieron dos fuerzas fundamentales: la electromagnética y la débil, creando la teoría electrodébil.

Sin embargo, el modelo estándar de la física de partículas no se estableció por completo hasta los años 70. En 1971, Gerardus 't Hooft y Martinus Veltman demostraron que las teorías con simetrías rotas podían ser renormalizadas. Además, el concepto de libertad asintótica, desarrollado por Frank Wilczek, David Gross y Hugh David Politzer en 1973, ayudó a entender las interacciones fuertes entre hadrones.

En los años 70, la teoría cuántica de campos también avanzó al descubrirse que algunas soluciones de las ecuaciones de campo, que no se podían calcular con los diagramas de Feynman, eran muy importantes. La idea de la renormalización también cambió, pasando de ser vista como un "problema" a ser una forma de entender que no sabemos todo lo que ocurre a distancias muy pequeñas.

Richard Feynman, Shin'ichirō Tomonaga y Julian Schwinger ganaron el premio Nobel de física en 1965 por desarrollar la electrodinámica cuántica.

Principios básicos de la teoría cuántica de campos

¿Por qué necesitamos la teoría cuántica de campos?

Limitaciones de la mecánica cuántica normal

En la mecánica cuántica "normal", se describe un grupo de partículas con una "función de onda" que nos dice la probabilidad de encontrar cada partícula en un lugar. Sin embargo, este método no funciona bien para algunos sistemas físicos:

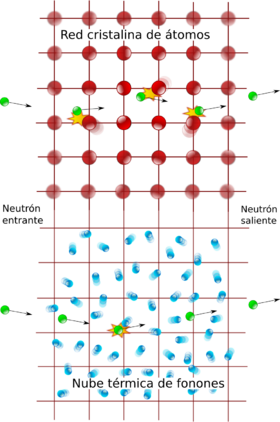
• Creación y destrucción de partículas: En la mecánica cuántica normal, el número de partículas es siempre el mismo. Pero en experimentos de alta energía, las partículas pueden desintegrarse o aniquilarse, lo que cambia el número de partículas. Por ejemplo, un electrón y un positrón pueden desaparecer y convertirse en fotones. En la física del estado sólido, las vibraciones de los átomos se ven como "cuasipartículas" (como los fonones), cuyo número también puede variar.

• Relatividad: La ecuación de la mecánica cuántica normal no es compatible con la relatividad especial de Einstein, que es fundamental para describir partículas que se mueven muy rápido.

• Campos clásicos: En la física clásica, las interacciones entre partículas no siempre son solo "fuerzas a distancia". A veces, es necesario considerar también los campos que generan, como el campo electromagnético que crean las cargas eléctricas en movimiento.

Se intentó modificar la ecuación de Schrödinger para que fuera compatible con la relatividad, pero estas nuevas ecuaciones tenían problemas, como predecir partículas con energía negativa. Esto se debe a que no consideraban que las partículas pudieran crearse o destruirse.

¿Qué es la teoría cuántica de campos?

Una teoría cuántica de campos es lo que obtenemos al aplicar las reglas de la cuantización a un campo clásico. Esto nos permite estudiar cómo se comportan los campos continuos (como el campo electromagnético) a nivel cuántico.

Cuando cuantizamos un campo, descubrimos que sus posibles estados son como los de un grupo de partículas idénticas que pueden aparecer y desaparecer. Además, si la ecuación del campo clásico respeta la teoría de la relatividad, el sistema cuántico resultante también lo hará. Así, la cuantización de un campo clásico resuelve los problemas que la mecánica cuántica "normal" no puede describir.

La segunda cuantización

El proceso de aplicar las reglas de cuantización a un campo y ver sus estados cuánticos como un grupo de partículas se llama segunda cuantización.

El límite continuo

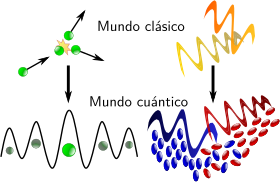
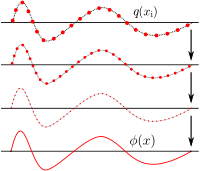
En la física clásica, un campo continuo es como un conjunto de muchos osciladores (como resortes) conectados entre sí. Por ejemplo, un sólido elástico puede describirse como un campo continuo (su densidad o tensión) o como una red de partículas unidas por "muelles" imaginarios. La descripción como campo es una aproximación de la descripción como osciladores cuando la distancia entre las partículas es muy pequeña.

Esta idea también se aplica a cómo evolucionan estos sistemas. Las vibraciones de los átomos en un sólido (visto como osciladores) son una mezcla de sus "modos normales" (vibraciones colectivas simples). Visto como un campo continuo, las ondas de densidad del sólido son una mezcla de "ondas planas" (las ondas más simples). Cada modo normal de los osciladores se corresponde con una onda plana del campo.

Osciladores acoplados	Límite continuo	Campo continuo
Dinámica en términos de:		Dinámica en términos de:
Modos normales	Límite continuo	Ondas planas

Aunque algunos campos clásicos, como el electromagnético, no son el límite de un sistema mecánico, la idea de que sus ecuaciones son similares a las de un sistema de osciladores abstractos sigue siendo válida.

Osciladores cuánticos

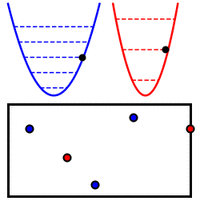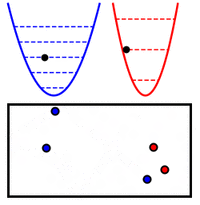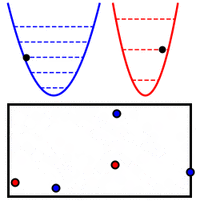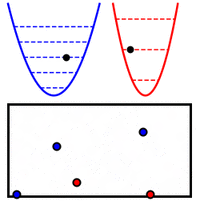
La energía en un oscilador armónico cuántico (un "resorte" cuántico) solo puede tener ciertos valores, que son múltiplos de su frecuencia ω. En un sistema de osciladores cuánticos conectados, la energía total es la suma de la energía de cada modo normal, como si fueran osciladores independientes.

Esto es muy parecido a la energía de un sistema de muchas partículas distribuidas en diferentes niveles de energía. Si identificamos cada nivel de energía con un modo normal y la cantidad de partículas en un nivel con el nivel de excitación de ese modo, las dos expresiones para la energía son equivalentes. Esto significa que un conjunto de osciladores cuánticos conectados se comporta como un sistema de partículas cuánticas cuyo número puede variar.

Límite continuo. Una cadena de átomos que vibran se puede ver como un campo continuo φ(x).

Modos normales. Las vibraciones colectivas más simples de un sistema físico, como las de esta membrana elástica. Modo (0,1).

Segunda cuantización. Un sistema de dos osciladores cuánticos es como un sistema con un número variable de partículas de dos tipos.

Campo cuántico

Un campo cuántico puede verse como el límite continuo de un grupo de osciladores cuánticos conectados. Como la energía de estos osciladores se comporta como la de un sistema de partículas, un campo cuántico es equivalente a un conjunto de partículas cuyo número puede cambiar.

Osciladores acoplados	Límite continuo	Campo continuo
se cuantiza en		se cuantiza en
Osc. cuánticos acoplados	Límite continuo	Campo cuántico

Cómo se comporta el campo cuántico

Campo cuántico libre

Cuando un campo cuántico es "libre" (sus ecuaciones son simples), se comporta exactamente como un sistema de osciladores armónicos conectados. La energía del campo es la suma de la energía de cada partícula individual. Como no hay interacciones, las partículas son libres y su número no cambia.

El estado de un campo cuántico se describe diciendo cuántas partículas hay en cada nivel de energía posible. Por ejemplo, una partícula en el primer nivel, cero en el segundo, dos en el tercero, etc. El estado sin ninguna partícula se llama el vacío.

Una característica importante es que estas partículas son indistinguibles. Si tienes una partícula en el nivel 1 y otra en el nivel 2, intercambiarlas no crea un estado diferente. Además, el número de partículas en un nivel puede ser muy alto, lo que significa que estas partículas son bosones. Para describir fermiones (otro tipo de partículas), se necesitan algunas modificaciones en el método de segunda cuantización.

Fermiones

Existen partículas llamadas fermiones, como el electrón y el protón, que siguen el principio de exclusión de Pauli. Esto significa que en un mismo nivel de energía solo puede haber una partícula. El método básico de segunda cuantización no impone este límite y no puede describir fermiones directamente.

La forma en que se cuantiza un campo determina si las partículas resultantes son bosones o fermiones. Para obtener fermiones, se usan reglas de "anticommutación" en lugar de las reglas normales. La elección de estas reglas no es arbitraria, sino que está relacionada con el espín de la partícula.

Espín y estadística

El tipo de campo que se cuantiza determina las propiedades de las partículas que aparecen, incluyendo su espín. Por ejemplo:

• Un campo escalar (que obedece la ecuación de Klein-Gordon) produce bosones de espín 0, como algunos mesones.
• Un campo espinorial (que obedece la ecuación de Dirac) produce fermiones de espín 1/2, como electrones o protones.
• Las ecuaciones del campo electromagnético (un campo vectorial) producen bosones de espín 1, los fotones.

Estas teorías de campos son relativistas, lo que significa que sus ecuaciones respetan la simetría Lorentz. Las partículas que surgen de ellas también son relativistas. Así, la teoría cuántica de campos puede describir partículas cuánticas que se mueven según la relatividad especial. También puede haber teorías cuánticas de campos no relativistas, como la que describe los fonones.

Estos ejemplos cumplen con una regla importante: el espín de un bosón siempre es un número entero, y el de un fermión siempre es un número semientero (como 1/2, 3/2, etc.). Si se intenta cuantizar un campo para obtener el tipo de partícula "incorrecto" (por ejemplo, fermiones de un campo escalar), los resultados no son consistentes. Esto se conoce como el teorema espín-estadística y es una consecuencia directa de combinar la mecánica cuántica y la relatividad especial.

Campo cuántico en interacción

Si la teoría de campos que se cuantiza es "no lineal", las partículas que se obtienen interactúan entre sí. En estas teorías, las ecuaciones del campo son más complejas e incluyen productos de campos. Esto significa que la energía del sistema tiene términos de interacción que no son simples. La mayoría de las teorías importantes en física incluyen estos términos de interacción.

Por ejemplo:

• La interacción de Yukawa describe las fuerzas entre nucleones (neutrones y protones) a través de piones.
• El campo de Higgs interactúa con todas las partículas elementales que tienen masa.
• La electrodinámica cuántica describe la interacción entre la luz (fotones) y partículas cargadas (como electrones).

Junto a cada producto de campos, hay una constante numérica llamada constante de acoplo, que indica la intensidad de la interacción. Por ejemplo, en la electrodinámica cuántica, la carga eléctrica del electrón es la constante de acoplo.

En una teoría de campos con interacciones, el número de partículas puede cambiar, lo que permite describir sistemas donde las partículas aparecen y desaparecen. Otra consecuencia de la interacción es la existencia de las antipartículas. Si las partículas de un sistema interactúan y tienen una carga que se conserva (como la carga eléctrica), la teoría cuántica de campos relativista necesita que exista una "copia" de cada partícula con la misma masa pero carga opuesta.

Formas alternativas de ver la teoría cuántica de campos

Existen otras maneras de entender y estudiar la teoría cuántica de campos. Una de ellas es el formalismo de la integral de caminos, que da los mismos resultados que la cuantización normal. Otra forma es derivar las leyes más generales que combinan la mecánica cuántica y la relatividad especial para describir las partículas subatómicas. Ambas formas son complementarias.

Desde un punto de vista matemático, la teoría cuántica de campos no es tan "rigurosa" como la mecánica cuántica más básica. Por eso, algunos matemáticos intentan estudiarla de forma más formal, buscando estructuras matemáticas que capturen sus características principales.

También hay versiones más generales de la teoría cuántica de campos. Por ejemplo, la teoría de campos a temperatura finita describe procesos donde las partículas se crean y destruyen a ciertas temperaturas. La teoría cuántica de campos en espacio-tiempo curvo es necesaria para describir un campo cuántico cuando hay gravedad.

Aspectos clave de la teoría cuántica de campos

Diagramas de Feynman

En los experimentos de física de altas energías, las partículas chocan a gran velocidad. La teoría cuántica de campos nos permite calcular los detalles de estas colisiones.

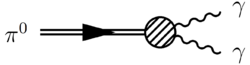
Los diagramas de Feynman son una forma gráfica de calcular la probabilidad de que ocurran estas colisiones. Estos diagramas muestran todas las posibles formas en que un proceso puede suceder. Las partículas que interactúan pueden emitir o absorber "partículas virtuales", que son las que transmiten las fuerzas entre ellas. Estas partículas virtuales existen por muy poco tiempo debido al principio de incertidumbre entre energía y tiempo. En realidad, las partículas virtuales son solo una idea para ayudarnos a calcular y no se pueden detectar. El proceso físico real es la suma de todos estos procesos virtuales.

Por ejemplo, en la dispersión Compton (cuando un electrón choca con un fotón), la probabilidad se calcula sumando las contribuciones de varios diagramas. En estos diagramas, las líneas curvas son fotones y las líneas rectas son electrones. Las líneas externas representan las partículas iniciales y finales, y las líneas internas representan las partículas virtuales. Los puntos donde las líneas se unen (vértices) representan la emisión o absorción de un fotón por un electrón.

La precisión del cálculo aumenta con el número de vértices en el diagrama. Los diagramas de Feynman son una herramienta fundamental en la física de partículas, ya que muestran los principios físicos más importantes y son esenciales para analizar las colisiones relativistas. Sin embargo, hay fenómenos que no pueden analizarse con estos diagramas.

Métodos funcionales y soluciones no perturbativas

El formalismo de la integral de caminos es otra forma de cuantizar un sistema, y da los mismos resultados que la cuantización normal. En este método, todas las posibles trayectorias que una partícula puede tomar contribuyen a la probabilidad de un evento. En la teoría cuántica de campos, la integral de caminos se usa para calcular la probabilidad de un proceso sumando las contribuciones de cada posible configuración del campo clásico.

Este método es útil para obtener las reglas de Feynman y analizar las simetrías del sistema. También es indispensable para estudiar las "soluciones no perturbativas".

Las soluciones no perturbativas son soluciones de las ecuaciones de campo donde las correcciones de la interacción no son pequeñas y no pueden aproximarse con los diagramas de Feynman. Todas las configuraciones clásicas del campo contribuyen a las probabilidades cuánticas, por lo que estas soluciones deben considerarse. Hay varios tipos de soluciones no perturbativas con diferentes efectos físicos:

• Los solitones (u ondas solitarias) son soluciones de ecuaciones de ondas no lineales que se propagan sin cambiar su forma. Una teoría de campos con solitones tiene dos tipos de partículas: las asociadas a los modos normales y las asociadas a los solitones.
• Los instantones son soluciones de las ecuaciones de campo que están concentradas alrededor de un punto en el espacio-tiempo. Son responsables de muchos efectos, como ciertas anomalías o el confinamiento en algunos modelos.

Otros ejemplos incluyen monopolos magnéticos, vortex lines, domain walls y skyrmiones.

Polarización del vacío. Una carga eléctrica "desnuda" (teórica) polariza el vacío, y los pares virtuales partícula-antipartícula la "cubren", resultando en una carga "física" finita.

Modelo de Ising. La renormalización permite estudiar sistemas físicos a diferentes escalas de energía. Los dipolos en el modelo de Ising pueden agruparse en "bloques" que interactúan en una versión "renormalizada" del sistema.

Renormalización

En los primeros usos de la teoría cuántica de campos, al calcular algunas cantidades, los resultados daban "infinito". Esto ocurría a menudo al intentar hacer los cálculos más precisos. Por ejemplo, el tercer diagrama de la dispersión Compton (mostrado antes) da un valor infinito.

La renormalización es un método para obtener valores finitos y medibles de estos cálculos infinitos. La solución es darse cuenta de que, en los cálculos, la teoría se aplica a distancias extremadamente cortas (o energías muy altas), lo que causa los infinitos.

En el ejemplo de la auto-energía del electrón (donde un fotón virtual es emitido y reabsorbido por un electrón), la suma de todas las contribuciones virtuales da un resultado infinito. Al reconocer que esta extrapolación es la causa del infinito, se puede identificar qué parte del resultado corresponde a la cantidad física real, que debe ser finita. Los infinitos desaparecen al considerar que deben "absorberse" en los parámetros de la teoría.

Este proceso implica usar una versión "regularizada" de la teoría, que es una aproximación sin infinitos. En esta teoría, se ve que las constantes iniciales (como la masa y la carga del campo) no son las mismas que la masa y la carga reales del electrón. Una vez que se establece la relación entre ellas, la fórmula se puede reescribir en términos de los parámetros físicos reales, y el resultado es finito.

Esta técnica, llamada grupo de renormalización, no solo es práctica, sino que también ofrece una nueva forma de ver los infinitos y la teoría de campos. La renormalización puede entenderse como el proceso de seleccionar las partes importantes de un proceso físico, ignorando las contribuciones que son demasiado lejanas en energía.

No todas las teorías permiten este proceso de absorber los infinitos. Las teorías que sí lo permiten se llaman "renormalizables", como las interacciones del modelo estándar. La interacción gravitatoria, sin embargo, no es renormalizable, lo que significa que para eliminar todos sus infinitos se necesitaría un número infinito de parámetros. Las teorías no renormalizables tienen menos poder de predicción, pero aun así se usan a menudo como teorías efectivas.

Teorías gauge

Cromodinámica cuántica como teoría gauge. Cada tipo de quark (u o d en la imagen) tiene tres "copias" de distinto "color". Los gluones actúan como bosones intermediarios entre partículas con color (como un fotón entre partículas con carga eléctrica).

Una teoría gauge es una teoría cuántica de campos con una estructura similar a la electrodinámica cuántica (QED). La QED es la versión cuántica de la electrodinámica clásica, que describe cómo interactúan las cargas eléctricas y la luz. En QED, las cargas eléctricas interactúan intercambiando fotones, que son los cuantos del campo electromagnético.

Las ecuaciones de Maxwell (de la electrodinámica clásica) tienen una propiedad llamada invariancia gauge. Esto significa que se pueden hacer ciertos cambios en el potencial electromagnético sin que el campo electromagnético real cambie. Esta propiedad se llama simetría local y es esencial para cuantizar las ecuaciones de forma consistente y obtener la QED.

Una teoría gauge no abeliana es una versión más general de la QED. En estas teorías, las partículas tienen múltiples "cargas" que se conservan, como la carga eléctrica. Estas partículas cargadas interactúan intercambiando varios bosones gauge intermediarios, que son similares al fotón. Sin embargo, en el caso no abeliano, estos bosones intermediarios también tienen carga e interactúan entre sí, a diferencia del fotón en QED. Los bosones gauge suelen ser sin masa, pero pueden adquirirla a través de un fenómeno llamado ruptura espontánea de simetría. Un ejemplo de teoría gauge no abeliana es la cromodinámica cuántica.

Las teorías gauge son una parte fundamental del modelo estándar de las partículas fundamentales. A nivel cuántico, tienen características únicas como el confinamiento (los quarks no pueden existir solos) y la libertad asintótica (los quarks interactúan débilmente a muy altas energías). La relatividad general también puede verse como una teoría gauge.

Simetrías, ruptura espontánea y anomalías

Simetrías aproximadas. Si las masas de los tres quarks u, d y s fueran iguales, existiría una simetría de sabor que clasifica los bariones ligeros (como el protón y el neutrón). Como sus masas son diferentes, la simetría no es perfecta, pero aún así ayuda a entender las diferencias de masa entre estos bariones.

Anomalías. Una simetría aproximada impedía que un pion se desintegrara en fotones. Se esperaba que ocurriera lentamente, pero en los años 60 se vio que era 1000 veces más rápido de lo previsto. Esto llevó al descubrimiento de las anomalías, ya que esa simetría no existe a nivel cuántico.

Las simetrías son muy importantes en física. Si las ecuaciones de movimiento de un sistema no cambian bajo ciertas transformaciones, esto significa que existen cantidades que se conservan. En la teoría cuántica de campos, las simetrías son cruciales. Por ejemplo, la invariancia Lorentz (una simetría relacionada con la relatividad) determina los tipos de partículas según su masa y espín. Las simetrías bajo transformaciones internas (como un cambio de fase) implican la conservación de cantidades como la carga eléctrica o la carga de color.

Incluso cuando una simetría no es perfecta, puede ser útil para entender un fenómeno. Además de las simetrías exactas y aproximadas, hay otras dos posibilidades interesantes: la ruptura espontánea de simetría y las anomalías.

La ruptura espontánea de simetría es un fenómeno común en sistemas cuánticos con infinitos grados de libertad, como la teoría cuántica de campos. Una simetría rota espontáneamente es aquella que, aunque es exacta en las leyes fundamentales, no se ve directamente porque los estados de menor energía del sistema no la respetan. Su presencia se manifiesta por la aparición de partículas llamadas bosones de Goldstone, o por bosones gauge masivos si la simetría es local.

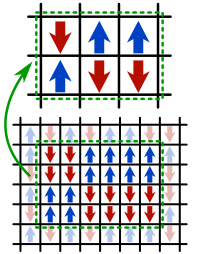
• Un ejemplo es un material ferromagnético. Por debajo de cierta temperatura, la magnetización del material apunta en una dirección específica. Aunque las leyes físicas son invariantes bajo rotaciones, el estado de menor energía tiene una dirección preferida. En este sistema, aparecen excitaciones colectivas llamadas magnones, que son los bosones de Goldstone.
• La ruptura espontánea de simetría es clave en el modelo estándar de la física de partículas, a través del mecanismo de Higgs. La fuerza electrodébil se explica con una teoría gauge que prohíbe que las partículas con carga débil tengan masa, pero en realidad sí la tienen. Las masas de estas partículas se explican por el valor del campo de Higgs a baja energía.

Las anomalías son violaciones de una simetría en un sistema cuántico que, a nivel clásico, sí tenía esa simetría. Son frecuentes en las teorías cuánticas de campos porque, para lidiar con los resultados infinitos, estas teorías deben ser "regularizadas", y este paso intermedio a menudo viola las simetrías.

• La anomalía conforme ocurre en teorías que clásicamente no cambian con la escala de distancias. En la teoría cuántica, esta simetría generalmente no se mantiene, ya que la intensidad de las fuerzas varía con la energía.
• La anomalía axial está relacionada con los números cuánticos que se conservan en el sistema. Por ejemplo, en el modelo estándar clásico, el número leptónico y el número bariónico se conservan, pero se ha demostrado que hay fenómenos que permiten que estos números cambien.

Las anomalías pueden indicar una inconsistencia en la teoría si afectan a una simetría gauge, ya que estas son fundamentales para eliminar partes no físicas del sistema.

Simetrías discretas: CPT

Algunas simetrías discretas son muy importantes en la teoría cuántica de campos, especialmente en la física de partículas. Esto se debe a que se descubrió que algunas interacciones fundamentales no respetan la paridad ni la conjugación de carga. Esto significa que se comportan de manera diferente si se ven en un espejo o si cada partícula se cambia por su antipartícula. Estas simetrías están relacionadas con la inversión temporal (cambiar la dirección del tiempo) a través del teorema CPT. Este teorema asegura que la combinación de estas tres operaciones deja inalterado cualquier sistema cuántico relativista.

Aplicaciones de la teoría cuántica de campos

Física de altas energías

Evento del quark top en CDF. El quark top fue la penúltima partícula del modelo estándar descubierta (en Tevatrón en 1995).

En la física de altas energías, se estudian los componentes más pequeños de la materia y cómo interactúan. Para ello, se necesita mucha energía para "romper" la materia. En este campo, es esencial usar la teoría cuántica de campos para describir el movimiento de las partículas a velocidades cercanas a la luz.

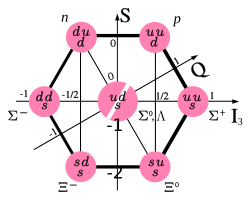
Actualmente, el modelo estándar describe los fenómenos conocidos a escala subatómica. Esta teoría clasifica los componentes fundamentales de la materia en tres familias de quarks (que forman los hadrones como el protón y el neutrón) y leptones (como el electrón y los neutrinos). Todas estas partículas son fermiones de espín 1/2 y, excepto los neutrinos, tienen carga eléctrica y masa.

El modelo estándar es una teoría gauge: las interacciones entre estas partículas ocurren mediante el intercambio de bosones gauge de espín 1. Todas las partículas (excepto los neutrinos) interactúan electromagnéticamente a través del fotón. Los quarks tienen "carga de color" y pueden intercambiar gluones. Además, todos estos fermiones tienen una carga llamada isoespín débil, que los hace interactuar a través de los bosones débiles Z⁰ y W^±. Estas tres interacciones se conocen como la interacción electromagnética, la interacción fuerte y la interacción débil.

El modelo estándar también incluye una partícula de espín 0 y sin carga llamada bosón de Higgs, cuya existencia está parcialmente confirmada. Esta partícula interactuaría con todas las que tienen masa, explicando por qué las partículas tienen masa, lo que parecía contradecir la conservación del isoespín débil.

El modelo estándar es muy preciso en sus predicciones, pero no explica algunos fenómenos, como el origen de la masa de los neutrinos, la naturaleza de la materia oscura o la interacción gravitatoria.

Física de la materia condensada

Un ejemplo básico de la segunda cuantización viene de la física del estado sólido: la descripción de las vibraciones de los átomos en un sólido como cuasipartículas llamadas fonones. En la física de la materia condensada, muchos sistemas se analizan de manera similar, aprovechando las técnicas de "muchos cuerpos", incluso si las partículas no se crean o destruyen realmente. La teoría de campos permite describir de forma efectiva las excitaciones colectivas de un sistema con muchas partículas en una fase específica.

Algunos ejemplos de problemas donde se aplica son la teoría BCS de la superconductividad, el efecto Hall cuántico o el ferromagnetismo y antiferromagnetismo. Muchos aspectos de la teoría cuántica de campos están presentes en estos fenómenos, como la ruptura espontánea de simetría y la invariancia gauge.

Algunas de estas propiedades de la teoría cuántica de campos se descubrieron o propusieron inicialmente en el contexto de la física de la materia condensada. Por ejemplo, el concepto de ruptura espontánea de simetría se desarrolló para explicar la superconductividad antes de ser adaptado al mecanismo de Higgs. La técnica del grupo de renormalización también aparece de forma natural en la materia condensada al analizar, por ejemplo, el modelo de Ising.

Superconductor. Levitación magnética de un imán sobre un superconductor.

Véase también

En inglés: Quantum field theory Facts for Kids