Tensor para niños
Un tensor es un concepto matemático que ayuda a describir cómo se relacionan diferentes cantidades en el espacio. Piensa en ellos como herramientas especiales que nos permiten entender cosas como las fuerzas que actúan sobre un objeto o cómo se mueve la energía.
Los tensores son muy útiles en la física y la ingeniería. Por ejemplo, se usan para estudiar:
- La tensión y la elasticidad de los materiales (cómo se estiran o se doblan).
- El movimiento de los fluidos (como el agua o el aire).
- El momento de inercia, que describe cómo un objeto gira.
- Fenómenos relacionados con la electricidad y el magnetismo.
- La relatividad general, una teoría de la gravedad de Albert Einstein.
En estas áreas, un tensor puede ser diferente en cada punto de un objeto. A esto se le llama un campo tensorial.
Matemáticos como Tullio Levi-Civita y Gregorio Ricci-Curbastro hicieron que los tensores fueran más conocidos alrededor del año 1900. Ellos continuaron el trabajo de otros, como Bernhard Riemann.
Contenido
¿Qué es un tensor?
Los tensores son una forma de describir relaciones complejas. Pueden representar cosas simples como números (escalares) o direcciones (vectores), pero también relaciones más complicadas.
Tensores como arreglos de números
Una forma sencilla de entender un tensor es como un arreglo de números, similar a una matriz (que es una tabla de números).
- Un número simple, como la temperatura, es un tensor de orden 0. No necesita dirección.
- Un vector, como la velocidad (que tiene magnitud y dirección), es un tensor de orden 1. Se puede representar como una lista de números.
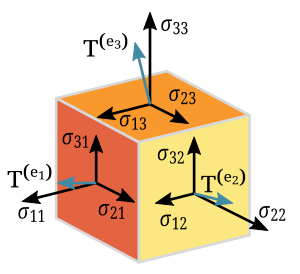
- Un tensor de orden 2 se puede ver como una tabla de números (una matriz). Por ejemplo, la tensión en un material se describe con un tensor de orden 2.
Los números dentro de un tensor se llaman sus componentes. Se identifican con índices, que son pequeños números o letras que indican su posición. Por ejemplo, si tenemos un tensor llamado T, sus componentes podrían ser Tij.
Cuando cambiamos la forma en que medimos las cosas (por ejemplo, si giramos nuestro sistema de coordenadas), los componentes de un tensor cambian de una manera específica. Esta forma de cambiar se llama ley de transformación. Es lo que hace que un tensor sea un tensor y no solo un montón de números al azar.
Tensores en el aprendizaje automático
Los tensores también son muy importantes en el campo del aprendizaje automático, especialmente en la inteligencia artificial. Por ejemplo, la biblioteca de programación TensorFlow, creada por Google, usa tensores para construir y entrenar redes neuronales.
En estas redes, los tensores son como los datos que fluyen entre diferentes "neuronas" artificiales, y las operaciones matemáticas se realizan sobre ellos. Esto permite a las computadoras aprender y reconocer patrones, como en el reconocimiento de imágenes o la traducción de idiomas.
TensorFlow es muy eficiente, especialmente en sistemas con muchas computadoras trabajando juntas, lo que se conoce como TensorFlow distribuido.
Galería de imágenes
-
El tensor de tensiones de Cauchy describe las fuerzas que experimenta un material en un punto. La imagen muestra las fuerzas en tres direcciones perpendiculares.
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
Véase también
En inglés: Tensor Facts for Kids
