John Wallis para niños
Datos para niños John Wallis |
||
|---|---|---|
 |
||
| Información personal | ||
| Nacimiento | 23 de noviembre de 1616jul. Ashford (Reino de Inglaterra) |
|
| Fallecimiento | 28 de octubre de 1703jul. Oxford (Reino de Inglaterra) |
|
| Sepultura | Iglesia de Santa María la Virgen | |
| Nacionalidad | Británico | |
| Religión | Presbiterianismo | |
| Familia | ||
| Padres | Rev. John Wallis Joanna Chapman |
|
| Educación | ||
| Educado en |
|
|
| Información profesional | ||
| Ocupación | Matemático, historiador de la matemática, filósofo, musicólogo, teórico de la música, criptólogo, profesor universitario y archivero | |
| Área | Matemáticas | |
| Conocido por | precursor cálculo infinitesimal, símbolo  |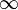
|
| Cargos ocupados | Cátedra saviliana de Geometría (1649-1703) | |
| Empleador |
|
|
| Obras notables | producto de Wallis | |
| Miembro de | Royal Society | |
John Wallis (nacido en Ashford, el 23 de noviembre de 1616 y fallecido en Oxford, el 28 de octubre de 1703) fue un matemático inglés muy importante. Se le reconoce por su contribución al desarrollo del cálculo, una rama de las matemáticas que estudia cómo cambian las cosas. Fue uno de los primeros en usar el símbolo 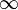para representar el infinito. Entre 1643 y 1689, trabajó como criptógrafo para el Parlamento y luego para la Corte real, descifrando mensajes secretos. También fue uno de los fundadores de la Royal Society, una sociedad científica muy prestigiosa, y profesor en la Universidad de Oxford.
Contenido
¿Quién fue John Wallis?
Sus primeros años y educación
John Wallis nació en Ashford, Kent, y fue el tercero de cinco hermanos. Su padre era el reverendo John Wallis. Comenzó sus estudios en la escuela de su localidad, pero tuvo que mudarse a la escuela de James Movat en Tenterden en 1625 debido a una epidemia de salud.
En 1631, en la escuela de Martin Holbeach en Felsted, tuvo su primer contacto con las matemáticas. Aunque le gustaban, en esa época las matemáticas no se veían como un estudio académico principal, sino más bien como algo práctico.
Su vida universitaria y primeros trabajos
En 1632, John Wallis fue enviado al Emmanuel College en Cambridge para estudiar. Allí, participó en un debate público sobre la circulación de la sangre, siendo una de las primeras veces que esta idea se discutía abiertamente en Europa. Sin embargo, su verdadero interés estaba en las matemáticas.
Obtuvo su primer título universitario en 1637 y una maestría en 1640. Después, se unió al sacerdocio. En 1644, recibió una beca para estudiar en el Queen's College de Cambridge. Se casó con Susana Glyde el 14 de marzo de 1645.
Durante este tiempo, Wallis colaboró con un grupo político, ayudándolos a descifrar mensajes secretos de sus oponentes. En esa época, la criptografía (el arte de escribir y descifrar códigos) no era muy avanzada. Wallis logró hacer los sistemas de cifrado mucho más seguros, incluso describiéndolos como indescifrables. También le preocupaba que otros países usaran estos métodos, por lo que rechazó enseñar criptografía a estudiantes de Hanóver en 1697.
Su regreso a Londres y la Royal Society
En 1643, Wallis fue nombrado capellán en Londres. Allí, se unió a un grupo de científicos que más tarde fundarían la Royal Society. Por fin pudo dedicarse a sus intereses matemáticos. En pocas semanas de 1647, dominó un importante libro de matemáticas llamado Clavis Mathematicae de William Oughtred.
Pronto, Wallis empezó a escribir sus propios trabajos. A lo largo de su vida, hizo grandes aportaciones a la trigonometría, el cálculo, la geometría y el estudio de las series infinitas.
Últimos años y otros intereses
John Wallis apoyó una propuesta para evitar un evento político importante, lo que le causó problemas con otro grupo político. A pesar de esto, en 1649 fue nombrado profesor de Geometría en la Universidad de Oxford, donde vivió hasta su fallecimiento el 28 de octubre de 1703.
Además de sus trabajos en matemáticas, Wallis también escribió sobre teología (el estudio de la religión), lógica, gramática inglesa y filosofía. Fue uno de los pioneros en introducir en Inglaterra un sistema de enseñanza para personas sordas, inspirado en el método del español Juan de Pablo Bonet.
Las contribuciones de John Wallis a las matemáticas
¿Cómo definió las secciones cónicas?
En 1655, Wallis publicó un trabajo sobre las secciones cónicas, que son formas como círculos, elipses, parábolas e hipérbolas. Fue el primer libro en el que estas curvas se definieron usando ecuaciones, lo que ayudó a aclarar ideas de matemáticos anteriores como René Descartes.
¿Qué es el Arithmetica Infinitorum?
En 1656, se publicó Arithmetica Infinitorum, la obra más importante de Wallis. En este libro, mejoró y organizó los métodos de análisis de otros matemáticos.
Una de sus grandes ideas fue desarrollar una forma estándar de escribir las potencias, extendiéndolas más allá de los números enteros positivos para incluir números racionales (fracciones):
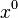
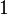
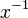
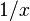
(la raíz cuadrada)![x^{p/q} = \sqrt[q]{x^p}](/images/math/3/3/8/338dcfe4d08e573cf2965b3398cfc7bd.png)
(raíces y potencias combinadas)
Wallis usó estas ideas para calcular el área bajo curvas. Demostró que la relación entre el área bajo una curva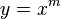 
y un paralelogramo de la misma base y altura era 
.
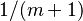¿Qué es el producto de Wallis?
Wallis también investigó cómo calcular el área de un cuarto de círculo. Aunque no conocía el teorema del binomio, que le habría ayudado, usó un método ingenioso llamado interpolación.
A través de un proceso complejo, llegó a una fórmula para calcular el valor de π (pi), que es una constante matemática muy importante. Esta fórmula se conoce hoy como el producto de Wallis:
En la misma obra, también habló sobre las fracciones continuas, que son expresiones matemáticas que se extienden infinitamente.
¿Cómo contribuyó al estudio de las curvas?
En 1659, Wallis publicó un trabajo con soluciones a problemas sobre las cicloides, que son curvas que se forman al rodar un círculo. Explicó cómo sus principios podían usarse para calcular la longitud de curvas algebraicas.
Dio una solución para calcular la longitud de la parábola semicúbica x³ = ay², descubierta por su alumno William Neil en 1657. Antes de esto, se pensaba que ninguna curva podía rectificarse (calcular su longitud), excepto el círculo. El trabajo de Neil y Wallis fue una novedad importante.
¿Qué aportó a la física y el álgebra?
En 1668, la Royal Society propuso estudiar la teoría de la colisión de los cuerpos. Wallis, junto con Christopher Wren y Christiaan Huygens, ofreció soluciones correctas. Sus soluciones se basaban en la conservación del momento lineal, que es una ley fundamental de la física. Wallis también consideró las colisiones en las que los objetos no rebotan perfectamente.
En 1685, Wallis publicó su libro Algebra, que incluía una historia de la materia. La segunda edición, de 1693, fue mucho más grande. Este libro es importante porque fue el primero en usar fórmulas de manera sistemática.
Wallis también es reconocido por la idea de la recta de números enteros, donde los números se representan en una línea: los números positivos a la derecha y los números negativos a la izquierda.
Obras importantes de John Wallis
- Arithmetica infinitorum, Oxford, 1656
- Opera, 1670-1671
- Treatise of Algebra, Londres, 1685
- Mathesis Universalis, Oxford, 1685
- De sectionibus conicis
- Operum mathematicorum pars prima, Oxford, 1657
- Tractatus Prœmialis. De loquela, sive Literarum omnium Formatione & genuino Sono, Oxford, Leon Lichfield, 1653. (Un tratado sobre el habla y la formación de sonidos).
- Grammatica Linguae Anglicanae, cui praefigitur de loquela sive de sonorum omnium loquelarum formatione tractatus grammatico physicus, Oxford, Leon Lichfield, 1653. (Una gramática de la lengua inglesa con un tratado sobre la formación de sonidos).
Galería de imágenes
-
Opera mathematica, 1657
Véase también
En inglés: John Wallis Facts for Kids
