Posición para niños
En física, la posición de una partícula nos dice dónde se encuentra en el espacio. Para saber su posición, usamos sistemas de coordenadas, que son como un mapa con un punto de partida.
En la mecánica, que estudia cómo se mueven los objetos, la posición de una partícula se describe con respecto a un punto de referencia. Imagina que es como decir "está a 5 metros al norte de la escuela".
En teorías más avanzadas, como la relatividad general, la idea de posición es un poco más compleja. El espacio puede ser "curvo", así que no siempre podemos usar un simple vector (una flecha que indica dirección y distancia) para señalar dónde está algo. En su lugar, se usan coordenadas especiales.
En la mecánica cuántica, que estudia el mundo muy, muy pequeño (como los átomos), la posición de una partícula es aún más difícil de definir. A veces, no podemos saber su posición exacta debido a principios fundamentales de la física.
En general, la palabra posición se usa para describir el estado o la situación de algo, ya sea un objeto grande o una partícula diminuta. Es como decir en qué punto de un proceso o de un diagrama se encuentra un sistema.
Contenido
¿Qué es el Vector de Posición en la Mecánica Clásica?
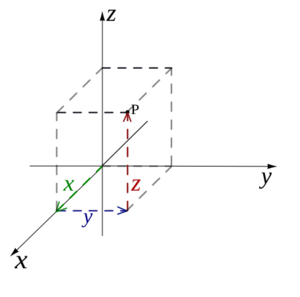
En la mecánica clásica, que es la física que usamos para describir el movimiento de objetos cotidianos, la posición de una partícula se representa con algo llamado vector de posición o radio vector. Piensa en él como una flecha que va desde un punto de inicio (llamado origen) hasta el lugar donde está la partícula. Se suele representar con la letra r o con las coordenadas del punto.
Las coordenadas son como las direcciones en un mapa. Por ejemplo, en un sistema de coordenadas cartesianas, se usan los valores (x, y, z) para decir dónde está un punto en el espacio.
Cuando una partícula se mueve de un lugar a otro, la diferencia entre su posición inicial y final se llama vector desplazamiento. Nos dice cuánto y en qué dirección se movió.
¿Cómo funcionan los Sistemas de Referencia?
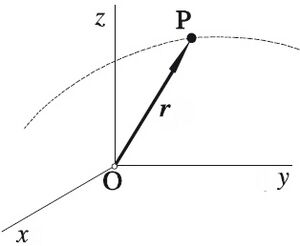
Para saber la posición de algo, necesitamos un punto de partida y unas direcciones. Esto es lo que llamamos un sistema de referencia. Es como tener un mapa con un origen (el punto "O") y unos ejes (como las líneas de una cuadrícula).
El vector de posición de un punto "P" se dibuja desde el origen "O" hasta el punto "P". Sus componentes son las coordenadas (x, y, z) del punto "P". Así, podemos escribir el vector de posición como:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf r = \mbox{OP} = x \mathbf i +y \mathbf j +z \mathbf k \,
Aquí, i, j y k son como pequeñas flechas que nos indican las direcciones de los ejes x, y, z. Un sistema de referencia se define por su origen y estas direcciones. Si las direcciones son perpendiculares entre sí, el sistema es "ortogonal".
¿Qué pasa si el Sistema de Referencia se mueve o gira?
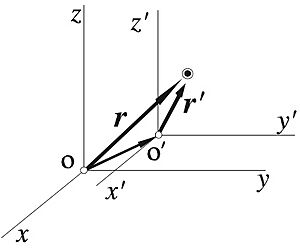
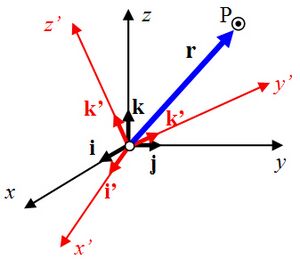
Si cambiamos el sistema de referencia, la forma en que describimos la posición de un punto también cambia.
- Traslación: Si movemos el origen de nuestro sistema de referencia (como si moviéramos el mapa a otro lugar sin girarlo), el vector de posición del punto "P" cambiará. La relación entre el vector de posición en el sistema original (O) y el nuevo (O') es:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{r} = \mbox{OO}' + \mathbf{r}'\,
Esto significa que las coordenadas del punto "P" no son las mismas si cambias el punto de partida de tu mapa.
- Rotación: Si giramos el sistema de referencia (como si giráramos el mapa), las componentes del vector de posición también cambiarán. Necesitaríamos una "matriz de rotación" para calcular las nuevas coordenadas.
¿Cómo cambia la Posición con el Tiempo?
Si una partícula está quieta, su posición no cambia con el tiempo y su vector de posición es constante:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{r} = x\mathbf{i} +y\mathbf{j} +z\mathbf{k}
Pero si la posición de una partícula cambia con el tiempo, podemos escribir su vector de posición como una función del tiempo:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{r}(t)=x(t)\mathbf{i}+y(t)\mathbf{j}+z(t)\mathbf{k}
Para saber qué tan rápido cambia la posición, calculamos su derivada con respecto al tiempo. Esto nos da la velocidad de la partícula. Si el sistema de referencia está fijo, la velocidad se obtiene simplemente derivando cada una de las coordenadas:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{v}(t)= \frac{d\mathbf{r}(t)}{dt} = \frac{dx(t)}{dt}\mathbf{i}+ \frac{dy(t)}{dt}\mathbf{j} + \frac{dz(t)}{dt}\mathbf{k}
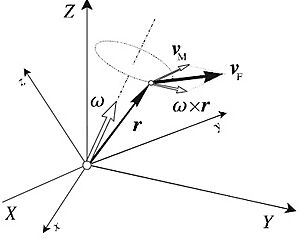
¿Qué pasa con la Posición en Sistemas de Referencia que Giran?
Si describimos el movimiento de una partícula desde un sistema de referencia que está girando (como si estuviéramos en un carrusel y tratáramos de describir el movimiento de algo fuera de él), el vector de posición sigue siendo el mismo, pero sus componentes (x, y, z) ahora dependen del tiempo porque los ejes del sistema de referencia están girando.
Cuando calculamos la velocidad en un sistema de referencia que gira, aparecen términos adicionales debido a la rotación. Esto es más complejo, pero la idea es que la velocidad que vemos depende de si nuestro propio "mapa" está girando.
Posición en la Mecánica Relativista
En la teoría especial de la relatividad, que estudia objetos que se mueven muy rápido, la posición se describe usando un "cuadrivector". Este vector incluye no solo las tres dimensiones del espacio (x, y, z) sino también el tiempo (t). Se ve así:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{X} = (X^0, X^1, X^2, X^3) = (ct, x, y, z)\,
Donde 'c' es la velocidad de la luz. La derivada de este cuadrivector con respecto a un "tiempo propio" (un tipo especial de tiempo) nos da la "cuadrivelocidad", que es el equivalente relativista de la velocidad.
Sin embargo, en la teoría general de la relatividad, las cosas se complican aún más. En esta teoría, el espacio-tiempo puede ser curvo (como una sábana estirada que se deforma por el peso de una bola). Por eso, no podemos usar un simple vector para describir la posición de un punto. Aunque podemos usar coordenadas especiales, no se pueden interpretar como un vector simple.
Posición en la Mecánica Cuántica
En la mecánica cuántica, que estudia el comportamiento de las partículas muy pequeñas (como electrones o fotones), no siempre podemos hablar de la posición exacta de una partícula o de su trayectoria. Esto se debe a un principio llamado "principio de incertidumbre de Heisenberg".
En esta teoría, las coordenadas se usan para describir la "función de onda" de un sistema, que nos da la probabilidad de encontrar una partícula en un lugar determinado, pero no su posición exacta en todo momento. Es como si la partícula no tuviera una posición fija hasta que la medimos.
Véase también
 En inglés: Position (geometry) Facts for Kids
En inglés: Position (geometry) Facts for Kids