Dinámica para niños
La dinámica es una parte de la física que estudia por qué los objetos se mueven o cambian de estado. Imagina que quieres saber por qué una pelota rueda o por qué un coche acelera; la dinámica se encarga de entender las fuerzas que causan esos cambios. Su objetivo es describir qué factores hacen que un sistema físico cambie, medirlos y crear "recetas" (ecuaciones) para predecir cómo se moverá o cambiará ese sistema.
La dinámica es muy importante en el estudio de cómo se mueven las cosas, como los coches o los planetas. También se usa en otras áreas de la física, como el estudio del calor (termodinámica) o la electricidad (electrodinámica). Aquí nos centraremos en cómo la dinámica explica el movimiento de los objetos.
La forma más conocida de estudiar el movimiento se llama mecánica newtoniana. Se basa en las ideas del científico Sir Isaac Newton del siglo XVII. Otros matemáticos como Gottfried Wilhelm Leibniz y Leonhard Euler también ayudaron a desarrollar las herramientas matemáticas para describir cómo se mueven los cuerpos cuando una fuerza actúa sobre ellos. Más tarde, otros científicos como Euler, Joseph-Louis Lagrange y William Rowan Hamilton crearon métodos más avanzados usando el concepto de energía. Estos avances, principalmente en los siglos XVIII y XIX, son la base de casi toda la física moderna.
Si conocemos con mucha precisión cómo está un objeto en un momento dado, la mecánica clásica nos permite predecir cómo se moverá en el futuro y cómo se movió en el pasado. Sin embargo, en la vida real, nunca podemos saber todo con absoluta precisión. Además, la teoría del caos nos enseña que las predicciones a muy largo plazo pueden no ser exactas.
La mecánica clásica funciona muy bien para objetos grandes que no son extremadamente pesados y que no se mueven a velocidades cercanas a la velocidad de la luz. Pero si los objetos son muy pequeños, como los átomos, necesitamos otra rama de la física llamada mecánica cuántica. Si los objetos se mueven muy rápido, cerca de la velocidad de la luz, usamos la relatividad especial. Y si los objetos son increíblemente pesados, como los planetas o las estrellas, se aplica la relatividad general.
Contenido
Dinámica: ¿Por qué se mueven las cosas?
Los Pioneros de la Dinámica
Desde hace mucho tiempo, la gente se ha preguntado por qué las cosas se mueven.
Aristóteles y el Movimiento
Uno de los primeros en pensar en esto fue el filósofo griego Aristóteles. Él veía el movimiento como el momento en que algo que podía ser de una forma, se convertía en esa forma. Por ejemplo, una semilla tiene la posibilidad de ser un árbol, y el movimiento es cuando se convierte en árbol.
Aristóteles estudió primero las causas del movimiento y luego el movimiento en sí. Esto hizo que fuera difícil avanzar en el conocimiento del movimiento por mucho tiempo.
Galileo y Newton: Las Bases Modernas
Fue gracias a científicos como Galileo Galilei e Isaac Newton que se pudo entender mejor el movimiento. Los experimentos de Galileo sobre cómo los objetos caen y aceleran ayudaron a Newton a crear sus famosas leyes del movimiento. Newton las publicó en su libro principal, Philosophiae Naturalis Principia Mathematica.
Hoy en día, los científicos usan las leyes de Newton para resolver la mayoría de los problemas de movimiento. Sin embargo, hay algunas excepciones. Las ecuaciones de Newton no son tan precisas cuando un objeto se mueve a velocidades muy altas, cercanas a la velocidad de la luz, o cuando los objetos son extremadamente pequeños, como las partículas dentro de un átomo.
¿Cómo se Calcula el Movimiento?
Para entender y predecir el movimiento, la dinámica usa "ecuaciones de movimiento". Para problemas sencillos, se usan directamente las leyes de Newton y las leyes de conservación.
La ley más importante en dinámica es la segunda ley de Newton. Dice que la fuerza total que actúa sobre un objeto es igual al cambio en su cantidad de movimiento a lo largo del tiempo.
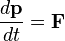
Aquí, F es la suma de todas las fuerzas y p es la cantidad de movimiento del objeto. Esta ecuación funciona para una partícula o un objeto rígido.
Las Leyes de Conservación
Las leyes de conservación son principios muy importantes en física. Nos dicen que algunas cantidades, como la energía, el movimiento o el giro, se mantienen constantes en un sistema si se cumplen ciertas condiciones. Esto significa que su valor no cambia con el tiempo.
- El teorema de la cantidad de movimiento dice que, si las fuerzas entre partículas solo dependen de la distancia entre ellas y actúan en la línea que las une, la cantidad de movimiento total del sistema se mantiene.
- El teorema del momento cinético (o momento angular) dice que, bajo condiciones similares, el cambio en el giro de un objeto es igual a la suma de los "momentos de fuerza" (que hacen girar las cosas) que actúan sobre él.
Estas leyes nos ayudan a entender cómo evolucionan los sistemas sin tener que resolver ecuaciones complicadas directamente.
Diferentes Maneras de Entender el Movimiento
Existen varias formas de escribir las ecuaciones de movimiento para predecir cómo se moverá un sistema mecánico, dependiendo de cómo empieza y qué fuerzas actúan sobre él.
- La mecánica newtoniana usa ecuaciones que describen las fuerzas y el movimiento en un sistema de coordenadas simple. Es útil para problemas muy sencillos.
- La mecánica lagrangiana usa ecuaciones que se adaptan mejor a la forma del problema. Permite usar coordenadas más generales y es útil para encontrar leyes de conservación.
- La mecánica hamiltoniana es similar a la lagrangiana, pero sus ecuaciones son más sencillas de resolver y permiten encontrar aún más fácilmente las leyes de conservación.
- El método de Hamilton-Jacobi es una forma avanzada de resolver problemas cuando ya se conocen algunas leyes de conservación.
Estos enfoques también se usan en la teoría de la relatividad y para estudiar materiales que se deforman o fluidos, aunque el cálculo es más complejo. La mecánica cuántica también usa un lenguaje matemático más avanzado.
Tipos de Sistemas en Dinámica
En física, hay dos tipos principales de sistemas: los que tienen un número limitado de partes (como un grupo de partículas) y los campos (como el campo gravitatorio). Los primeros se describen con un número limitado de ecuaciones, mientras que los campos necesitan ecuaciones más complejas.
La mayoría de los sistemas mecánicos son del primer tipo. Sin embargo, algunos, como los fluidos (líquidos y gases) o los sólidos deformables, se describen mejor como campos. Incluso los cuerpos rígidos (que no se deforman) pueden describirse con un número limitado de ecuaciones, aunque estén hechos de muchísimas partículas.
La Dinámica de una Partícula
Esta parte de la mecánica newtoniana estudia sistemas como si fueran puntos muy pequeños que interactúan entre sí con fuerzas que actúan a distancia.
En la teoría de la relatividad, no se puede simplemente usar las posiciones de las partículas en cada momento, porque las acciones a distancia instantáneas no son posibles. La fuerza sobre una partícula depende de las posiciones que tuvieron las otras partículas en el pasado.
La Dinámica de un Cuerpo Rígido
La mecánica de un sólido rígido estudia el movimiento y el equilibrio de objetos que no se deforman. Es un modelo matemático útil para entender cómo se mueven objetos como una rueda o una puerta, aunque en la realidad todos los objetos se deforman un poco. Un sólido rígido es un conjunto de puntos que se mueven de tal manera que las distancias entre ellos no cambian, sin importar las fuerzas que actúen.
¿Y los Fluidos y Materiales Deformables?
Otros objetos, como los sólidos deformables (como una goma elástica) o los fluidos (como el agua o el aire), no pueden describirse con un número limitado de coordenadas. Necesitan funciones que describan lo que ocurre en cada punto de ellos. Esto hace que las ecuaciones para estudiarlos sean mucho más complicadas.
Conceptos Clave en Dinámica
La Inercia: La Resistencia al Cambio
La inercia es la tendencia de los objetos a mantener su estado de reposo o de movimiento uniforme, a menos que una fuerza externa actúe sobre ellos. Piensa en un balón de fútbol: si está quieto, tiende a quedarse quieto; si está rodando, tiende a seguir rodando.
En física, un sistema tiene más inercia si es más difícil cambiar su estado. Los dos tipos de inercia más comunes son la inercia mecánica y la inercia térmica.
- La inercia mecánica mide lo difícil que es cambiar el movimiento o el reposo de un objeto. Depende de la masa del objeto y de cómo está distribuida esa masa.
- La inercia térmica mide lo difícil que es cambiar la temperatura de un objeto cuando entra en contacto con otros o se calienta. Depende de la masa y de su capacidad para almacenar calor.
Las "fuerzas de inercia" son fuerzas que parecen existir cuando un observador está en un sistema que se está moviendo o acelerando, pero en realidad no son fuerzas reales.
La masa inercial es una medida de cuánto se resiste un objeto a cambiar su velocidad. Cuanta más masa inercial tiene un objeto, más difícil es acelerarlo o frenarlo.
Trabajo y Energía: Motores del Cambio
El trabajo y la energía son conceptos muy importantes en la mecánica. El principal teorema que los relaciona es el teorema de la energía cinética. Este teorema dice que el trabajo realizado sobre un objeto es igual al cambio en su energía de movimiento (energía cinética).
Gracias a este teorema, podemos conectar la mecánica con otras ciencias como la química o la electricidad, lo que lo hace fundamental.
Fuerza y Potencial: Las Causas del Movimiento
En dinámica, las causas del cambio se representan con fuerzas o con un concepto relacionado llamado energía potencial. En la mecánica clásica y relativista, se usa mucho el concepto de fuerza. En la mecánica cuántica, es más común hablar de energía potencial.
La fuerza total F sobre un sistema mecánico clásico se relaciona con el cambio en su cantidad de movimiento P de esta manera:
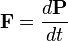
Si un sistema mecánico conserva su energía, la energía potencial V y la energía cinética K (energía de movimiento) se relacionan así:
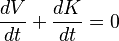
Esto significa que la suma de la energía potencial y la energía cinética se mantiene constante.
Sistemas Dinámicos
La teoría de sistemas dinámicos es una parte de las matemáticas que estudia las propiedades de las ecuaciones que describen cómo evolucionan los sistemas con el tiempo. Está relacionada con la teoría del caos, que explora cómo pequeños cambios pueden llevar a resultados muy diferentes.
Véase también
 En inglés: Classical mechanics Facts for Kids
En inglés: Classical mechanics Facts for Kids
- Invariancia galileana
- Dinámica de una partícula en mecánica newtoniana
- Dinámica de sistemas
- Estática

