Historia de la mecánica de fluidos para niños

La historia de la mecánica de fluidos es el relato de cómo hemos aprendido sobre los fluidos, que son líquidos y gases, y las fuerzas que actúan sobre ellos. Es una parte de la física que estudia cómo se mueven y se comportan. Desde la antigüedad, los seres humanos han usado los fluidos, pero la mayoría de las ideas y teorías modernas se descubrieron en Europa durante los siglos XVII y XVIII.

Antes de que se estudiara de forma científica, la mecánica de fluidos ya se usaba mucho en la vida diaria. Por ejemplo, para regar los cultivos, construir canales o hacer fuentes. Cuando las personas empezaron a vivir en un solo lugar (sedentarización), necesitaron controlar el agua. El riego a pequeña escala comenzó hace unos 6500 años antes de Cristo. Grandes obras hidráulicas como canales y sistemas de riego por gravedad aparecieron alrededor del año 3000 a.C. En esa época, ya se inventaron herramientas para medir el nivel de las inundaciones, se secaban zonas pantanosas y se construían presas y diques para protegerse de las crecidas de ríos como el Nilo, el Amarillo y el Éufrates. Los acueductos más antiguos podrían haberse construido en Creta en el segundo milenio a.C. y en Palestina en el siglo XI a.C.

El estudio del agua y su comportamiento no pasó de las aplicaciones prácticas a la teoría hasta mucho después. En la ciudad de Alejandría, en el siglo III a.C., Arquímedes estudió con los alumnos de Euclides. Al regresar a Siracusa, formuló principios que son la base de la estática de fluidos, especialmente su famoso principio. En el siglo I d.C., Heron de Alejandría continuó este trabajo, descubriendo el principio de la presión y, sobre todo, el caudal (la cantidad de fluido que pasa por un lugar en un tiempo dado).

Durante la Antigüedad tardía, se siguieron construyendo grandes obras hidráulicas. Se mejoraron los acueductos, los sistemas de distribución de agua y saneamiento, y también las fuentes y los baños. Estas obras fueron descritas por Frontino. En Europa, durante la Edad Media, parte del conocimiento sobre hidrostática (fluidos en reposo) e hidráulica (fluidos en movimiento) del antiguo Imperio Greco-Romano se perdió. Sin embargo, se conservó y desarrolló en el mundo islámico, donde se tradujeron por primera vez las obras de Arquímedes y Euclides.

En cuanto a las construcciones hidráulicas, la Edad Media vio la desaparición del sistema de riego de Mesopotamia debido a las invasiones mongolas, lo que causó una gran disminución de la población local. Pero también en el siglo VII d.C., bajo la dinastía Sui, se inició la primera etapa de las obras del Gran Canal de China, que uniría el norte y el sur de China.

La mecánica de fluidos volvió a estudiarse en Europa con los trabajos de Leonardo da Vinci en el siglo XV. Él describió muchos tipos de flujo y formuló el principio de conservación de la masa (también llamado principio de continuidad), siguiendo los pasos de Herón. Leonardo sentó las bases de esta disciplina e introdujo muchas ideas de hidrodinámica, como las líneas de corriente. Entendiendo la resistencia al flujo, diseñó el paracaídas, el anemómetro (para medir la velocidad del viento) y la bomba centrífuga.

Aunque Simon Stevin (1548-1620) descubrió importantes principios de la hidrostática, completando el trabajo de Arquímedes, no los presentó de forma clara. Fue Blaise Pascal quien, en su obra de 1648, dio una presentación organizada de estos principios fundamentales de la hidrostática. Las demostraciones de la paradoja hidrostática se usan para enseñar este fenómeno. Uno de los experimentos más conocidos es la explosión del barril de Pascal.

El Libro II de los Principia Mathematica de Isaac Newton, que trata sobre el movimiento de los cuerpos en ambientes con resistencia, no aportó un conocimiento científico nuevo y significativo en este campo. Sin embargo, según Clifford Truesdell, el trabajo de Newton estableció un plan de estudio que se siguió durante cincuenta años. Las leyes de la mecánica de fluidos no empezaron a establecerse realmente hasta el trabajo de Alexis Claude Clairaut (1713-1765) y Jean le Rond D'Alembert (1717-1783).

La mecánica de fluidos ganó profundidad con la llegada de las matemáticas a la física. En 1738, Daniel Bernoulli estableció leyes para fluidos no viscosos usando el principio de conservación de la energía mecánica. El desarrollo del cálculo diferencial permitió a Jean le Rond D'Alembert en 1749 sentar las bases de la hidrodinámica. Él presentó el principio de la presión interna de un fluido, el campo de velocidades y las derivadas parciales aplicadas a los fluidos. Leonhard Euler completó el análisis de D'Alembert sobre la presión interna y las ecuaciones de la dinámica de fluidos incompresibles. En 1755, publicó un tratado con ecuaciones diferenciales parciales que describían los fluidos incompresibles perfectos. Poco antes, en 1752, D'Alembert había notado la paradoja que lleva su nombre: mostraba que las ecuaciones contradecían la práctica, pues un cuerpo sumergido en un fluido se movería sin resistencia según la teoría, lo cual la observación desmentía. Esto se resolvió cuando Henri Navier en 1820 introdujo el concepto de fricción en las ecuaciones matemáticas de la mecánica de fluidos. George Gabriel Stokes en 1845 llegó a una ecuación que describía el flujo de un fluido viscoso. Las ecuaciones de Navier-Stokes marcarían el resto de la historia de la mecánica de fluidos.

Estos avances continuaron en la segunda mitad del siglo XVIII y la primera del siglo XX:

• Se desarrollaron conceptos como la capa límite por Ludwig Prandtl, muy útil para la aerodinámica y la hidrodinámica naval.
• Se estudió el nuevo campo de los flujos supersónicos (más rápidos que el sonido).
• Se investigaron los flujos en medios porosos por Henry Darcy y las interfaces agua-aire por Moritz Weber.
• Se estudiaron las inestabilidades y la turbulencia, un tema que aún no está completamente resuelto. En este campo surgieron escuelas fundadas por pioneros como Prandtl en Göttingen o la escuela rusa de matemáticos de Kolmógorov.

Durante este período, Ludwig Boltzmann abrió un nuevo capítulo con la descripción estadística de los gases a nivel microscópico. Esto fue desarrollado por Martin Knudsen para el dominio inaccesible a una descripción continua. David Enskog y Sydney Chapman mostraron cómo pasar de la descripción molecular a la continua para los gases, permitiendo calcular coeficientes de transporte (difusión, viscosidad, conducción) a partir de la interacción molecular. Todos estos trabajos teóricos se basaron en los estudios fundamentales previos de matemáticos como Leonhard Euler, Augustin Louis Cauchy o Bernhard Riemann.

Además, el desarrollo de muchas instalaciones de prueba y herramientas de medición permitió obtener numerosos resultados. No todos pudieron explicarse con la teoría, y aparecieron muchos números adimensionales que ayudaban a entender y justificar las pruebas realizadas con maquetas en un túnel de viento o en un tanque de carena. Dos mundos científicos coexistieron y a menudo se ignoraron hasta finales del siglo XIX. Esa brecha desapareció gracias a personas como Theodore von Kármán o Ludwig Prandtl a principios del siglo XX. Todos estos avances fueron impulsados por el desarrollo industrial: hidrodinámica industrial, construcción naval y aeronáutica.

El cálculo numérico, que surgió en la segunda mitad del siglo XX, permitió el nacimiento de una nueva rama de la mecánica de fluidos: la mecánica de fluidos computacional. Esta se basa tanto en la aparición de computadoras cada vez más potentes como en nuevos métodos matemáticos. La capacidad de cálculo permite realizar "experimentos numéricos" que compiten con los medios de prueba o facilitan su interpretación. Este tipo de enfoque se usa comúnmente en el estudio de la turbulencia.

El segundo hecho importante en este período es el aumento considerable del número de personas dedicadas a la investigación y el desarrollo. Los descubrimientos se han convertido más en el trabajo de equipos que de individuos. Estos equipos son principalmente estadounidenses; Europa (especialmente Francia, Reino Unido y Alemania) ha perdido su liderazgo.

Los campos industriales que justifican estos desarrollos son la meteorología, la climatología, la geofísica o incluso la oceanografía y la astrofísica. Estos campos solo existen gracias al cálculo numérico, al menos los dos primeros.

Antigüedad

Prehistoria

Las civilizaciones antiguas mostraron un conocimiento práctico, aunque no científico, del flujo de fluidos. Esto se ve en el diseño de flechas, lanzas, barcos y, especialmente, en proyectos de ingeniería hidráulica para protegerse de inundaciones, para riego, drenaje y suministro de agua. Las primeras civilizaciones humanas surgieron cerca de las orillas de los ríos. Por eso, el inicio de la hidrología, la hidráulica y la ingeniería hidráulica coincidió con ellas.

China

Los antiguos filósofos chinos registraron observaciones sobre la gravedad específica y la flotabilidad. En el siglo IV a.C., Mencio describió que el peso del oro es equivalente al de las plumas. En el siglo III d.C., Cao Chong contó la historia de cómo pesó un elefante observando cuánto se hundían los barcos cargados con diferentes pesos.

Arquímedes

Las fuerzas que actúan en la flotabilidad descubiertas por Arquímedes. El objeto flota porque la fuerza de flotación hacia arriba es igual a la fuerza de la gravedad hacia abajo.

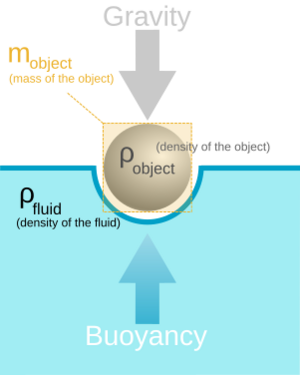
Los principios fundamentales de la hidrostática (fluidos en reposo) y la dinámica (fluidos en movimiento) fueron establecidos por Arquímedes en su obra Sobre los cuerpos flotantes, alrededor del año 250 a.C. En ella, Arquímedes desarrolló la ley de la flotabilidad, también conocida como Principio de Arquímedes. Este principio dice que un cuerpo sumergido en un fluido experimenta una fuerza hacia arriba igual al peso del fluido que desplaza. Arquímedes sostenía que cada parte de un fluido, cuando estaba en equilibrio, era presionada por igual en todas las direcciones. También investigó las condiciones bajo las cuales un cuerpo sólido que flota en un fluido debería adoptar y mantener una posición de equilibrio.

La escuela alejandrina

En la escuela griega de Alejandría, que prosperó bajo el apoyo de los Ptolomeos, se hicieron intentos de construir maquinaria hidráulica. Alrededor del año 120 a.C., Ctesibio y Herón inventaron la fuente de compresión, el sifón y la bomba de pistón. El sifón es un dispositivo sencillo, pero la bomba de fuerza es un invento complicado, que difícilmente se habría esperado en los inicios de la hidráulica. Probablemente fue sugerida a Ctesibio por la rueda egipcia o noria, que era común en ese momento. Esta era una especie de bomba de cadena, que consistía en una serie de ollas de barro transportadas por una rueda. En algunas de estas máquinas, las ollas tenían una válvula en el fondo que les permitía descender sin mucha resistencia y disminuía mucho la carga sobre la rueda. Si se asume que esta válvula se introdujo ya en la época de Ctesibio, no es difícil ver cómo tal máquina pudo haber llevado a la invención de la bomba de fuerza.

Sexto Julio Frontino

A pesar de estas invenciones de la escuela de Alejandría, su atención no parece haberse centrado en el movimiento de los fluidos. El primer intento de investigar este tema fue realizado por Sexto Julio Frontino, inspector de las fuentes públicas en Roma durante los reinados de Nerva y Trajano. En su obra De aquaeductibus urbis Romae commentarius, consideró los métodos que se usaban en ese momento para determinar la cantidad de agua descargada de tuberías y cómo distribuir el agua de un acueducto o una fuente. Observó que el flujo de agua de un orificio dependía no solo del tamaño del orificio, sino también de la altura del agua en el depósito. También notó que un tubo usado para sacar agua de un acueducto debía, según las circunstancias, tener una posición más o menos inclinada respecto a la dirección original de la corriente. Pero como no conocía la ley de las velocidades del agua corriente que depende de la profundidad del orificio, la falta de precisión en sus resultados no es sorprendente.

Mundo islámico

Físicos islámicos

Los científicos islámicos, especialmente Abu Rayhan Biruni (973-1048) y más tarde Al-Khazini (activo entre 1115-1130), fueron los primeros en aplicar métodos científicos experimentales a la mecánica de fluidos. Esto fue particularmente importante en el campo de la estática de fluidos, por ejemplo, para determinar pesos específicos. Aplicaron teorías matemáticas de proporciones y técnicas infinitesimales, e introdujeron métodos algebraicos y de cálculo avanzado en la estática de fluidos.

En estática de fluidos, Biruni descubrió que existe una relación entre la gravedad específica de un objeto y el volumen de agua que desplaza. También introdujo el método de verificar las pruebas durante los experimentos y midió los pesos de varios líquidos. Registró las diferencias de peso entre el agua dulce y el agua salada, y entre el agua caliente y el agua fría. Durante sus experimentos sobre mecánica de fluidos, Biruni inventó la medida cónica para encontrar la relación entre el peso de una sustancia en el aire y el peso del agua desplazada.

Al-Khazini, en El libro de la balanza de la sabiduría (1121), inventó una balanza hidrostática.

Ingenieros islámicos

En el siglo IX, el Libro de mecanismos ingeniosos de los hermanos Banū Mūsā describía una serie de controles automáticos tempranos en la mecánica de fluidos. Los hermanos Banu Musa desarrollaron controles de nivel de dos pasos para fluidos, una forma temprana de controles de estructura variable discontinua. También describieron uno de los primeros controladores de retroalimentación para fluidos. Según Donald Routledge Hill, los hermanos Banu Musa eran "maestros en el uso de pequeñas variaciones" en las presiones hidrostáticas y en el uso de válvulas cónicas como componentes "en línea" en sistemas de flujo, "el primer uso conocido de válvulas cónicas como controladores automáticos". También describieron el uso de otras válvulas, incluyendo una válvula de tapón, una válvula de flotador y un grifo. Los Banu Musa también desarrollaron un sistema temprano a prueba de fallos en el que "se pueden extraer pequeñas cantidades de líquido repetidamente, pero si se retira una gran cantidad, no es posible realizar más extracciones". El sifón doble concéntrico y el embudo con el extremo doblado para verter diferentes líquidos, ninguno de los cuales aparece en obras griegas anteriores, también fueron inventos originales de los hermanos Banu Musa. Algunos de los otros mecanismos que describieron incluyen una cámara flotante y un sensor de presión.

En 1206, el Libro del conocimiento de ingeniosos dispositivos mecánicos de Al-Jazari describía muchas máquinas hidráulicas. De particular importancia fueron sus bombas elevadoras de agua. El primer uso conocido de un cigüeñal en una bomba de cadena fue en una de las máquinas saqiya de al-Jazari. El concepto de minimizar el trabajo intermitente también está implícito por primera vez en una de las bombas de cadena saqiya de al-Jazari, cuyo propósito era maximizar la eficiencia de la bomba de cadena saqiya. Al-Jazari también inventó una bomba de succión de pistón alternativo de dos cilindros, que incluía la primera bomba de succión en tuberías, bombeo de succión, bombeo de doble acción y uso temprano de válvulas y un cigüeñal - mecanismo de biela. Esta bomba fue notable por tres razones: el primer uso conocido de una tubería de succión verdadera (que succionaba fluidos en un vacío parcial) en una bomba, la primera aplicación del principio de doble acción y la conversión de movimiento rotatorio en alternativo, a través del mecanismo cigüeñal-biela.

Siglos XVII y XVIII

Castelli y Torricelli

Benedetto Castelli y Evangelista Torricelli, dos de los alumnos de Galileo, aplicaron los descubrimientos de su maestro a la ciencia de la hidrodinámica. En 1628, Castelli publicó una pequeña obra, Della misura dell'acque correnti, donde explicaba satisfactoriamente varios fenómenos del movimiento de los fluidos en ríos y canales. Sin embargo, cometió un error al suponer que la velocidad del agua era proporcional a la profundidad del orificio debajo de la superficie del recipiente. Torricelli, al observar que en un chorro el agua que salía por un pequeño orificio subía casi a la misma altura que el depósito del que provenía, imaginó que debía moverse con la misma velocidad que si hubiera caído desde esa altura por la fuerza de la gravedad. De ahí dedujo que las velocidades de los líquidos son como la raíz cuadrada de la altura, sin contar la resistencia del aire y la fricción del orificio. Este teorema se publicó en 1643, al final de su tratado De motu gravium projectorum, y fue confirmado por los experimentos de Raffaello Magiotti sobre las cantidades de agua descargadas desde diferentes orificios bajo diferentes presiones (1648).

Blaise Pascal

Gracias a Blaise Pascal, la hidrostática se convirtió en una ciencia. En un tratado sobre el equilibrio de los líquidos (Sur l’équilibre des liqueurs), encontrado entre sus manuscritos después de su muerte y publicado en 1663, demostró las leyes del equilibrio de los líquidos de la manera más sencilla, ampliamente confirmadas por experimentos.

Mariotte y Guglielmini

El teorema de Torricelli fue usado por muchos autores posteriores, pero especialmente por Edme Mariotte (1620-1684). Su Traité du mouvement des eaux, publicado después de su muerte en 1686, se basa en una gran variedad de experimentos bien realizados sobre el movimiento de los fluidos, hechos en Versailles y Chantilly. En la discusión de algunos puntos, cometió errores importantes. Otros aspectos los trató muy superficialmente, y en ninguno de sus experimentos aparentemente prestó atención a la disminución del flujo que surge de la contracción de la vena líquida cuando el orificio es solo una perforación en una placa delgada. Pero parece haber sido el primero en intentar atribuir la diferencia entre la teoría y el experimento al retraso de la velocidad del agua debido a la fricción. Su contemporáneo Domenico Guglielmini (1655-1710), inspector de ríos y canales en Bolonia, había atribuido esta disminución de la velocidad en los ríos a los movimientos transversales que surgen de las irregularidades en su fondo. Pero como Mariotte observó obstrucciones similares incluso en tuberías de vidrio donde no podían existir corrientes transversales, la causa aducida por Guglielmini parecía sin fundamento. El filósofo francés, por lo tanto, consideró estas obstrucciones como los efectos de la fricción. Supuso que los filamentos de agua que rozaban los lados del tubo perdían parte de su velocidad; que los filamentos contiguos, al tener por esto mayor velocidad, rozaban sobre los primeros y sufrían una disminución de su rapidez; y que los demás filamentos se veían afectados con retrasos similares proporcionales a su distancia al eje de la tubería. De esta manera, la velocidad media de la corriente podía disminuir.

Estudios de Isaac Newton

Fricción y viscosidad

Los efectos de la fricción y la viscosidad en la disminución de la velocidad del agua corriente se estudiaron en los Principia de Isaac Newton, quien aportó mucha luz a varias ramas de la hidromecánica. En una época en que el sistema cartesiano de vórtices era universalmente aceptado, consideró necesario estudiar esa hipótesis. En sus investigaciones, demostró que la velocidad de cualquier capa del vórtice era un promedio entre las velocidades de las capas que la rodeaban. De esto se seguía que la velocidad de un filamento de agua que se mueve en un tubo es un promedio entre las velocidades de los filamentos que lo rodean. Aprovechando estos resultados, Henri Pitot, ingeniero francés de origen italiano, demostró después que los retrasos que surgen de la fricción son inversamente proporcionales a los diámetros de las tuberías en las que se mueve el fluido.

Orificios

La atención de Newton también se dirigió a la descarga de agua a través de los orificios en el fondo de los recipientes. Supuso un recipiente cilíndrico lleno de agua con un pequeño orificio en su fondo por donde escapaba el agua, y que el recipiente se abastecía de agua de tal manera que siempre permanecía lleno a la misma altura. Luego supuso que esa columna cilíndrica de agua se dividía en dos partes: la primera, a la que llamó "catarata", era un hiperboloide (una forma geométrica) generado por la rotación de una hipérbola de quinto grado alrededor del eje del cilindro que debía pasar por el orificio, y la segunda, el resto del agua en el recipiente cilíndrico. Consideró que las capas horizontales de este hiperboloide estaban siempre en movimiento, mientras que el resto del agua estaba en reposo, e imaginó que había una especie de catarata en medio del fluido.

Cuando se compararon los resultados de esta teoría con la cantidad de agua realmente descargada, Newton concluyó que la velocidad con la que salía el agua por el orificio era igual a la que tendría un cuerpo que cae al descender a través de la mitad de la altura del agua en el depósito. Esa conclusión, sin embargo, era totalmente incompatible con el hecho conocido de que los chorros de agua se elevan casi a la misma altura que sus depósitos, y Newton parece haber sido consciente de esa objeción. Por ello, en la segunda edición de sus Principia, que apareció en 1713, reconsideró su teoría. Había descubierto una contracción en la vena de líquido (vena contracta) que salía del orificio, y encontró que, a la distancia de aproximadamente un diámetro de la abertura, la sección de la vena se contrajo en la proporción subduplicada de dos a uno. Consideró, por tanto, que la sección de la vena contraída era el verdadero orificio del que debe deducirse la descarga de agua, y que la velocidad del agua que salía era la debida a la caída desde la altura total del agua en el depósito; y por este medio su teoría se volvió más conforme a los resultados de la experiencia, aunque todavía con serias objeciones.

Ondas

Newton también fue el primero en investigar el difícil tema del movimiento de las ondas.

Daniel Bernoulli

Portada de Hydrodynamica, obra de 1738 de Daniel Bernoulli

En 1738, el matemático, médico y físico suizo Daniel Bernoulli (1700-1782), miembro de la familia Bernoulli, publicó su Hydrodynamica seu de viribus et motibus fluidorum commentarii. Su teoría del movimiento de los fluidos —cuyo inicio fue publicado por primera vez en sus memorias tituladas Theoria nova de motu aquarum per canales quocunque fluentes, comunicada a la Academia de San Petersburgo ya en 1726—, se basaba en dos suposiciones que le parecían conformes a la experiencia. Supuso que la superficie del fluido contenido en un recipiente que se vaciaba por un orificio permanecía siempre horizontal. Y, si la masa fluida se dividía en un número infinito de capas horizontales del mismo volumen, que esas capas permanecían unidas entre sí, y que todos sus puntos descendían verticalmente, con velocidades inversamente proporcionales a su anchura, o a las secciones horizontales del depósito. Para determinar el movimiento de cada capa, empleó el principio de la conservatio virium vivarum (conservación de las fuerzas vivas), y obtuvo soluciones muy elegantes. Pero al no haber una demostración general de ese principio, sus resultados no inspiraron la confianza que de otro modo habrían merecido, y se hizo deseable tener una teoría más segura y que dependiera únicamente de las leyes fundamentales de la mecánica. Colin Maclaurin y John Bernoulli, que eran de esta opinión, resolvieron el problema por métodos más directos, uno en su Fluxions, publicado en 1742, y el otro en su Hydraulica nunc primum detecta, et demonstrata directe ex fundamentis pure technicis, que forma el cuarto volumen de sus obras. Se ha pensado que el método empleado por Maclaurin no es suficientemente riguroso; y el de John Bernoulli era, en opinión de Lagrange, defectuoso en claridad y precisión.

Jean le Rond d'Alembert

Nouvelles expériences sur la résistance des fluides.

La teoría de Daniel Bernoulli también fue cuestionada por el matemático y enciclopedista francés Jean le Rond d'Alembert (1717-1783). Al generalizar la teoría de los péndulos de Jacob Bernoulli, descubrió un principio de la dinámica tan simple y general que reducía las leyes del movimiento de los cuerpos a las de su equilibrio mecánico. Aplicó este principio al movimiento de los fluidos y dio una muestra de su aplicación al final de su Dynamics en 1743. Fue desarrollado más completamente en su Traité des fluides, publicado en 1744, en el que dio soluciones simples y elegantes de problemas relacionados con el equilibrio y el movimiento de los fluidos. Hizo uso de las mismas suposiciones que Bernoulli, aunque su cálculo se estableció de manera muy diferente. Consideró, en cada instante, el movimiento real de una capa como compuesto del movimiento que tenía en el instante anterior y del movimiento que había perdido; y las leyes del equilibrio entre los movimientos perdidos le proporcionaron las ecuaciones que representaban el movimiento del fluido.

Todavía era necesario expresar mediante ecuaciones el movimiento de una partícula del fluido en cualquier dirección. Esas ecuaciones fueron encontradas por d'Alembert a partir de dos principios: que un canal rectangular, tomado en una masa de fluido en equilibrio, está en equilibrio, y que una parte del fluido, al pasar de un lugar a otro, conserva el mismo volumen, cuando el fluido es incompresible, o se dilata de acuerdo con una ley dada cuando el fluido es elástico. Su ingenioso método, publicado en 1752, en su Essai sur la résistance des fluides, fue perfeccionado en sus Opuscules mathématiques, y fue adoptado por Leonhard Euler.

Leonhard Euler

La resolución de las cuestiones relativas al movimiento de fluidos se efectuó mediante los coeficientes diferenciales parciales de Leonhard Euler. Este cálculo fue aplicado por primera vez al movimiento del agua por d'Alembert y le permitió, tanto a él como a Euler, representar la teoría de los fluidos en fórmulas no restringidas por ninguna hipótesis particular.

Pierre Louis Georges Dubuat

Uno de los que trabajaron con más éxito en la ciencia de la hidrodinámica en esa época fue el ingeniero militar francés Pierre Louis Georges Dubuat (1734-1809). Siguiendo los pasos del abad Charles Bossut (Nouvelles Experiences sur la résistance des fluides, 1777), publicó, en 1786, una edición revisada de sus Principes d'hydraulique, que recogía una teoría satisfactoria del movimiento de los fluidos, basada únicamente en experimentos. Dubuat consideraba que si el agua fuera un fluido perfecto, y los canales por los que fluía infinitamente lisos, su movimiento sería continuamente acelerado, como el de los cuerpos que descienden en un plano inclinado. Pero dado que el movimiento de los ríos no se aceleraba continuamente y que pronto llegaba a un estado de uniformidad, era evidente que la viscosidad del agua y la fricción del canal por el que descendían debían de ser iguales a la fuerza aceleradora y contrarrestarla. Dubuat, por lo tanto, asumió como una proposición de fundamental importancia que, cuando el agua fluye en cualquier canal o lecho, la fuerza aceleradora que la obliga a moverse es igual a la suma de todas las resistencias que encuentra, ya derivasen de su propia viscosidad o del roce de su lecho. Este principio fue empleado por él en la primera edición de su obra, que apareció en 1779. La teoría contenida en esa edición se basaba en los experimentos de otros, pero pronto vio que una teoría tan nueva y que conducía a resultados tan diferentes de la teoría ordinaria, debía basarse en nuevos experimentos más directos que los anteriores, y se dedicó a hacerlos desde 1780 hasta 1783. Los experimentos de Bossut se realizaron solo en tuberías de una pendiente moderada, pero Dubuat usó declives de cada clase, e hizo sus experimentos sobre canales de varios tamaños.

Hermann von Helmholtz

Animación de la calle vórtice creada por un objeto cilíndrico; el flujo en lados opuestos del objeto recibe diferentes colores, lo que muestra que los vórtices se desprenden de lados alternos del objeto

Una mirada al efecto de la calle de vórtices de Von Kármán desde el nivel del suelo —extremadamente raro, ya que suelen verse solo desde el espacio—, mientras el aire fluye rápidamente desde el Pacífico hacia el este sobre las montañas del desierto de Mojave.

Una calle de vórtices en un líquido 2D de discos duros

En 1858, Hermann von Helmholtz publicó su importante artículo «Über Integrale der hydrodynamischen Gleichungen, welche den Wirbelbewegungen entsprechen». Este artículo fue tan importante que unos años más tarde, P. G. Tait publicó en 1867 una traducción al inglés, «Sobre las integrales de las ecuaciones hidrodinámicas que expresan el movimiento de vórtice». En su artículo, Helmholtz estableció sus tres "leyes del movimiento de vórtice" de la misma manera que se encuentran en cualquier libro de texto avanzado de mecánica de fluidos hoy en día. Este trabajo estableció la importancia de la vorticidad (el giro del fluido) en la mecánica de fluidos y en la ciencia en general.

Durante el siglo siguiente, la "dinámica de vórtices" maduró como un subcampo de la mecánica de fluidos, y siempre ocupó al menos un capítulo importante en los tratados sobre el tema. Así, el conocido Hydrodynamics de Horace Lamb (6ª ed., 1932) dedica un capítulo completo a la vorticidad y a la dinámica de vórtices, al igual que la Introducción a la dinámica de fluidos de G. K. Batchelor (1967). Con el tiempo, se dedicaron tratados completos al movimiento de los vórtices. Se pueden mencionar Théorie des Tourbillons de H. Poincaré (1893), Leçons sur la Théorie des Tourbillons de H. Villat (1930), The Kinematics of Vorticity de C. Truesdell (1954) y Vortex Dynamics de P. G. Saffman (1992). Al principio, se dedicaron sesiones individuales en las conferencias científicas a los vórtices, al movimiento de los vórtices, a la dinámica de los vórtices y a los flujos de los vórtices. Posteriormente, se dedicaron reuniones enteras al tema.

El alcance del trabajo de Helmholtz creció hasta abarcar los flujos atmosféricos y oceanográficos, todas las ramas de la ingeniería y de las ciencias aplicadas y, finalmente, los superfluidos (hoy incluidos los condensados de Bose-Einstein). En la mecánica de fluidos moderna, el papel de la dinámica de vórtices en la explicación de los fenómenos de flujo está firmemente establecido. Algunos vórtices conocidos han adquirido nombres y se muestran regularmente en los medios de comunicación populares: huracanes, tornados, trombas marinas, vórtices arrastrados por aeronaves (por ejemplo, vórtices en las puntas de las alas), vórtices en desagües (incluido el vórtice de la bañera), anillos de humo, anillos de burbujas de aire bajo el agua, vórtices de cavitación detrás de las hélices de los barcos, etc. En la literatura técnica, una serie de vórtices que surgen en condiciones especiales también tienen nombre: la estela de la calle de vórtices de Von Kármán detrás de un cuerpo rocoso, los vórtices de Taylor entre cilindros giratorios, los vórtices de Görtler en flujo a lo largo de una pared curva, etc.

Gaspar Riche de Prony

La teoría del agua corriente avanzó mucho gracias a las investigaciones de Gaspard Riche de Prony (1755-1839). A partir de una colección de los mejores experimentos realizados por estudiosos anteriores, seleccionó ochenta y dos (cincuenta y uno sobre la velocidad del agua en tuberías y treinta y uno sobre su velocidad en canales abiertos). Al analizarlos con principios físicos y mecánicos, logró establecer fórmulas generales que permitieron una expresión sencilla para la velocidad del agua corriente.

Johan Albert Eytelwein

J. A. Eytelwein de Berlín, quien publicó en 1801 un valioso compendio de hidráulica titulado Handbuch der Mechanik und der Hydraulik, investigó la descarga de agua mediante tuberías compuestas, los movimientos de chorros y sus impulsos contra superficies planas y oblicuas. Demostró teóricamente que una rueda hidráulica tendría su máximo efecto cuando su circunferencia se moviera con la mitad de la velocidad de la corriente.

Jean Nicolás Pierre Hachette y otros

J.N.P. Hachette en 1816-1817 publicó memorias que recogían los resultados de experimentos sobre el chorro de fluidos y la descarga de recipientes. Su objetivo era medir la parte contraída de una vena de fluido, examinar los fenómenos que acompañaban a la disposición de tubos adicionales e investigar la forma de la vena de fluido y los resultados obtenidos cuando se empleaban diferentes formas de orificios. Bajo la dirección del gobierno francés, J.V. Poncelet (1788-1867) y J. A. Lesbros (1790-1860) realizaron extensos experimentos sobre la descarga de agua de los orificios (Expériences hydrauliques, París, 1832).

P.P. Boileau (1811-1891) discutió sus resultados y añadió experimentos propios (Traité de la mesure des eaux courantes, París, 1854). K.R. Bornemann volvió a examinar todos estos resultados con mucho cuidado y dio fórmulas que expresan la variación de los coeficientes de descarga en diferentes condiciones (Civil Ingénieur, 1880). Julius Weisbach (1806-1871) también realizó muchas investigaciones experimentales sobre la descarga de fluidos.

Los experimentos de J. B. Francis (Lowell Hydraulic Experiments, Boston, Mass., 1855) le llevaron a proponer variaciones en las fórmulas aceptadas para la descarga sobre vertederos. Una generación más tarde Henri-Émile Bazin llevó a cabo una investigación muy completa sobre este tema. También Henry G. P. Darcy (1803-1858) llevó a cabo una elaborada investigación sobre el flujo de agua en tuberías y canales, que continuó Bazin, a expensas del gobierno francés (Recherches hydrauliques, París, 1866).

Andreas Rudolf Harlacher y otros

Los ingenieros alemanes también habían dedicado especial atención a la medición del caudal en los ríos. El Beiträge zur Hydrographie des Königreiches Böhmen (Praga, 1872-1875) de Andreas Rudolf Harlacher recogía valiosas medidas de ese tipo, junto con una comparación de los resultados experimentales con las fórmulas de caudal propuestas hasta la fecha de su publicación. Y más datos importantes fueron proporcionados por los aforos del Misisipi hechos para el gobierno de los Estados Unidos por Andrew Atkinson Humphreys y Henry Larcom Abbot, por los aforos de Robert Gordon del río Irrawaddy, y por los experimentos de Allen J.C. Cunningham en el canal Ganges. La fricción del agua, investigada para velocidades bajas por Coulomb, fue medida para velocidades más altas por William Froude (1810-1879), cuyo trabajo fue de gran valor en la teoría de la resistencia de los barcos (Brit. Assoc. Report., 1869), y el movimiento de la línea de corriente fue estudiado por los profesores Osborne Reynolds y Henry S. Hele-Shaw.

Desarrollos en la dinámica de vórtices

La dinámica de vórtices es un subcampo muy activo de la dinámica de fluidos, que atrae la atención en las principales conferencias científicas y da lugar a talleres y simposios dedicados completamente al tema.

Una curiosa desviación en la historia de la dinámica de los vórtices fue la teoría del vórtice del átomo de William Thomson, más tarde Lord Kelvin. Su idea básica era que los átomos debían representarse como movimientos de vórtice en el éter. Esta teoría fue anterior a la teoría cuántica por varias décadas y, debido a la posición científica de su creador, recibió una atención considerable. Durante la búsqueda de esta teoría se generaron muchos conocimientos profundos sobre la dinámica de los vórtices. Otros resultados interesantes fueron el primer conteo de nudos simples por parte de P. G. Tait, hoy considerado un esfuerzo pionero en teoría de grafos, topología y teoría de nudos. Finalmente, se vio que el átomo del vórtice de Kelvin estaba equivocado, pero los muchos resultados en la dinámica del vórtice que precipitó han resistido la prueba del tiempo. El propio Kelvin originó la noción de circulación y demostró que en un fluido no viscoso se conservaría la circulación alrededor de un contorno material. Este resultado, señalado por Einstein en "Zum hundertjährigen Gedenktag von Lord Kelvins Geburt, Naturwissenschaften, 12 (1924), 601–602", (traducción del título: "En el centenario del nacimiento de Lord Kelvin"), como uno de los resultados más significativos del trabajo de Kelvin, proporcionó un vínculo temprano entre la dinámica de fluidos y la topología.

La historia de la dinámica de vórtices parece particularmente rica en descubrimientos y redescubrimientos de resultados importantes, porque los resultados obtenidos se olvidaron por completo después de su descubrimiento y luego se redescubrieron décadas después. Así, la integrabilidad del problema de los vórtices de tres puntos en el plano quedó resuelta en la tesis de 1877 de un joven matemático aplicado suizo llamado Walter Gröbli. A pesar de haber sido escrito en Göttingen en el círculo general de científicos que rodeaban a Helmholtz y Kirchhoff, y a pesar de haber sido mencionado en las conocidas conferencias de Kirchhoff sobre física teórica y en otros textos importantes como la Hydrodynamics de Lamb, esta solución fue en gran parte olvidada. Un artículo de 1949 del destacado matemático aplicado J. L. Synge creó un breve renacimiento, pero el artículo de Synge fue a su vez olvidado. Un cuarto de siglo después, un artículo de E. A. Novikov de 1975 y un artículo de H. Aref de 1979 sobre la advección caótica finalmente sacaron a la luz este importante trabajo anterior. La elucidación posterior del caos en el problema de los cuatro vórtices y en la advección de una partícula pasiva por tres vórtices hizo que el trabajo de Gröbli fuera parte de la "ciencia moderna".

Otro ejemplo de este tipo es la llamada "aproximación de inducción localizada" (LIA) para el movimiento tridimensional de filamentos de vórtice, que ganó popularidad a mediados de la década de 1960 a través del trabajo de Arms, Hama, Betchov y otros, pero resultó ser una actualización de los primeros años del siglo XX en el trabajo de Da Rios, un estudiante talentoso del célebre matemático italiano T. Levi-Civita. Da Rios publicó sus resultados en varias formas, pero nunca fueron asimilados en la literatura de la mecánica de fluidos de su época. En 1972, H. Hasimoto usó las "ecuaciones intrínsecas" de Da Rios (más tarde redescubiertas de forma independiente por R. Betchov) para mostrar cómo el movimiento de un filamento de vórtice bajo LIA podría estar relacionado con la ecuación no lineal de Schrödinger. Esto inmediatamente hizo que el problema formara parte de la "ciencia moderna", ya que entonces se descubrió que los filamentos de vórtice pueden soportar ondas de torsión solitarias de gran amplitud.

Galería de imágenes

• 

  Personalidades de la historia de la mecánica de fluidos (lista no exhaustiva)

• 

  Grabado ilustrando el momento ¡Eureka! de Arquimedes

• 

  Una ilustración del experimento del barril de Pascal.

• 

  Una simulación por computador de un flujo de aire de alta velocidad alrededor de un transbordador espacial durante la reentrada.

• 

  Simulación numérica de la inestabilidad de Kelvin-Helmholtz.

Véase también