Principio de Arquímedes para niños
El principio de Arquímedes es una regla muy importante en la física que nos ayuda a entender por qué algunos objetos flotan y otros se hunden en líquidos o gases. Dice que cuando un objeto se sumerge en un fluido (como agua o aire), el fluido lo empuja hacia arriba con una fuerza igual al peso del fluido que el objeto mueve o "desaloja". Esta fuerza hacia arriba se llama empuje hidrostático o empuje de Arquímedes. Se mide en newtons.
La fórmula básica para entender el empuje es:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): E = \rho_\text{f}\;g\;V\;
Donde:
- E es el empuje (la fuerza hacia arriba).
- ρf es la densidad del fluido (qué tan "pesado" es el fluido por unidad de volumen).
- g es la gravedad (la fuerza que nos atrae hacia la Tierra).
- V es el volumen del fluido que el objeto ha movido.
Esto significa que el empuje depende de tres cosas: la densidad del fluido, el volumen del objeto sumergido y la gravedad del lugar. El empuje siempre actúa hacia arriba y se aplica en un punto especial del objeto llamado centro de carena.
Contenido
¿Quién fue Arquímedes y su Gran Descubrimiento?
Arquímedes fue un brillante matemático e inventor que vivió hace mucho tiempo en la antigua Grecia, en la ciudad de Siracusa. Su padre era astrónomo, así que Arquímedes creció rodeado de ciencia. Estudió en Alejandría, Egipto, un lugar famoso por su gran biblioteca y centro de estudios. Allí conoció a otros científicos importantes, como Eratóstenes.
Arquímedes se dedicó a estudiar muchas áreas, como las matemáticas, la física, la geometría y la astronomía. Hizo descubrimientos que todavía hoy son muy importantes.
La Historia de la Corona y el "¡Eureka!"
Una de las historias más famosas sobre Arquímedes cuenta cómo descubrió su principio. El rey Hierón II de Siracusa le pidió que averiguara si una nueva corona de oro puro que le habían hecho tenía plata mezclada. El rey no quería dañar la corona, así que Arquímedes no podía fundirla.
Mientras Arquímedes tomaba un baño, notó que el nivel del agua subía cuando él entraba en la tina. Se dio cuenta de que el volumen de agua que se desbordaba era igual al volumen de su propio cuerpo. Pensó que podría usar esta idea para medir el volumen de la corona. Si dividía el peso de la corona por el volumen de agua que desplazaba, obtendría su densidad. Si la densidad era menor que la del oro puro, significaría que le habían añadido otros metales.
¡Estaba tan emocionado con su descubrimiento que salió corriendo por las calles, gritando "¡Eureka!" (que en griego significa "¡Lo encontré!").
Aunque esta historia se ha contado por mucho tiempo, el científico Galileo Galilei en el siglo XVI propuso una forma más precisa de cómo Arquímedes pudo haber resuelto el problema, usando una balanza especial. Lo importante es que Arquímedes sí escribió sobre el principio de flotación en su libro Sobre los cuerpos flotantes.
Entendiendo el Empuje: La Fuerza Secreta del Agua
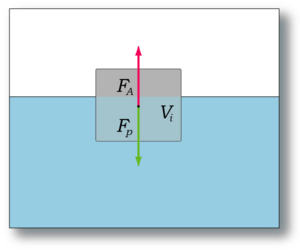
El principio de Arquímedes nos dice que un fluido ejerce una fuerza hacia arriba sobre cualquier objeto sumergido en él. Imagina que tienes una pelota de playa y la intentas hundir en una piscina. Sentirás una fuerza que la empuja hacia arriba, ¿verdad? Esa es la fuerza de empuje.
¿Qué es el Fluido Desplazado?
Cuando un objeto entra en un fluido, ocupa un espacio. Ese espacio que ocupa el objeto antes estaba lleno de fluido. A ese fluido que el objeto "quita" de su lugar se le llama "fluido desalojado" o "fluido desplazado". El principio de Arquímedes dice que la fuerza de empuje es exactamente igual al peso de ese fluido que el objeto movió.
Por ejemplo, si un barco pesa 1000 toneladas, para flotar debe desplazar 1000 toneladas de agua. El agua que el barco desplaza es la que lo empuja hacia arriba con la fuerza necesaria para que no se hunda.
¿Por Qué Flotan los Barcos y Submarinos?
El principio de Arquímedes es clave para entender por qué los objetos flotan. Un objeto flota si la fuerza de empuje que recibe es igual o mayor que su propio peso.
El Principio de Flotación en Acción
- Barcos: Un barco de acero es muy pesado, pero flota. ¿Cómo es posible? Su forma hueca hace que desplace un gran volumen de agua. Aunque el acero es más denso que el agua, el volumen total del barco (incluyendo el aire dentro del casco) hace que su densidad promedio sea menor que la del agua. Así, el peso del agua que desplaza es igual al peso del barco, y por eso flota.
- Submarinos: Los submarinos pueden flotar o sumergirse. Tienen tanques especiales que pueden llenar de agua o de aire. Para sumergirse, llenan los tanques de agua, lo que aumenta su peso y hace que se hunda. Para subir a la superficie, expulsan el agua de los tanques con aire comprimido, lo que disminuye su peso y hace que el empuje del agua sea mayor, permitiéndole flotar.
- Dirigibles y globos aerostáticos: Estos vehículos flotan en el aire, que también es un fluido. Se llenan de un gas más ligero que el aire (como helio o aire caliente). Al ser más ligeros, desplazan un volumen de aire más pesado que ellos mismos, y el empuje del aire los eleva.
Aplicaciones del Principio de Arquímedes en la Vida Real
Este principio no solo explica por qué flotan los barcos, sino que tiene muchas otras aplicaciones:
- Diseño de barcos y submarinos: Es fundamental para que puedan navegar de forma segura.
- Globos aerostáticos y dirigibles: Permite que se eleven y se mantengan en el aire.
- Hidrómetros: Son instrumentos que se usan para medir la densidad de líquidos, como la leche o el anticongelante, basándose en cuánto flotan.
- Chalecos salvavidas: Están diseñados para desplazar suficiente agua y generar un empuje que mantenga a la persona a flote.
Galería de imágenes
Véase también
 En inglés: Archimedes' principle Facts for Kids
En inglés: Archimedes' principle Facts for Kids