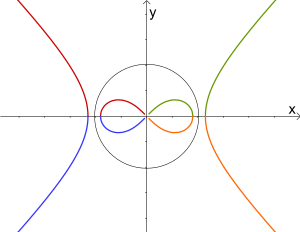Hipérbola para niños
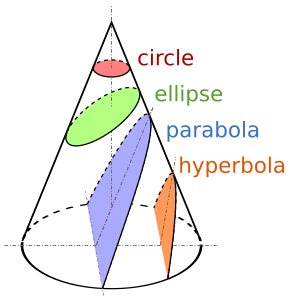
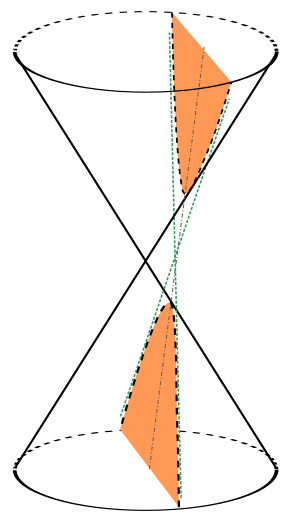
Una hipérbola (del griego antiguo hyperbolē) es una curva especial que tiene dos partes separadas, como si fueran dos "ramas" que se abren. Puedes imaginarla como la forma que obtienes si cortas un cono con un plano de una manera específica.
En geometría analítica, una hipérbola es el conjunto de todos los puntos en un plano donde la diferencia de sus distancias a dos puntos fijos, llamados focos, es siempre la misma. Esta diferencia es igual a la distancia entre los vértices de la hipérbola.
Contenido
¿De dónde viene la palabra "Hipérbola"?
La palabra "hipérbola" viene del griego "ὑπερβολή", que significa "exceso". Es la misma raíz que la palabra "hipérbole", que usamos en lenguaje para exagerar algo.
¿Quién descubrió las Hipérbolas?
Se dice que las formas cónicas, como la hipérbola, fueron descubiertas por un matemático griego llamado Menecmo (alrededor del 380 al 320 a.C.). Él las usó para resolver un problema antiguo de geometría. Otros matemáticos como Proclo y Eratóstenes también hablaron de ellas.
Sin embargo, el primero en usar la palabra "hipérbola" fue Apolonio de Perge. Él escribió un libro muy importante llamado Cónicas, donde estudió a fondo estas curvas y cómo se relacionan con las líneas tangentes.
¿Cómo se describen las Hipérbolas con ecuaciones?
Ecuaciones básicas en un plano de coordenadas
Las hipérbolas se pueden describir con ecuaciones matemáticas. Si el centro de la hipérbola está en el punto (0, 0) de un plano de coordenadas, sus ecuaciones más comunes son:
(1)Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{x^2}{a^2}-\frac{y^2}{b^2} = 1
o
(2)Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{y^2}{a^2}-\frac{x^2}{b^2} = 1
Aquí, `a` y `b` son números que nos dicen qué tan "abierta" o "cerrada" es la hipérbola. La ecuación () es para hipérbolas que se abren hacia los lados (a lo largo del eje `x`), y la () es para las que se abren hacia arriba y hacia abajo (a lo largo del eje `y`).
Hay una relación importante entre `a`, `b` y `c` (la distancia del centro a los focos):
(3)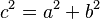
Ecuaciones para hipérbolas con centro en otro punto
Si el centro de la hipérbola no está en (0,0) sino en otro punto `C(h, k)`, las ecuaciones cambian un poco:
(4)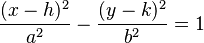
o
(5)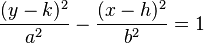
Estas ecuaciones nos ayudan a dibujar y entender la forma de la hipérbola en cualquier lugar del plano.
¿Qué es la Excentricidad de una Hipérbola?
La excentricidad (`e`) de una hipérbola es un número que nos dice qué tan "estirada" o "aplanada" es la curva. Se calcula así:
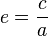
Donde `c` es la mitad de la distancia entre los focos y `a` es la mitad de la distancia entre los vértices. Como `c` siempre es mayor que `a` en una hipérbola, la excentricidad de una hipérbola siempre es mayor que 1.
Partes importantes de una Hipérbola
Eje transversal
Es el segmento de línea recta que conecta los dos Vértices de la hipérbola y pasa por los Focos. Su longitud es `2a`.
Eje conjugado
Es un segmento de línea recta que pasa por el centro de la hipérbola y es perpendicular al eje transversal. Su longitud es `2b`.
Eje focal
Es el segmento de línea recta que une los dos focos de la hipérbola. Su longitud es `2c`. Este eje está en la misma línea que el eje transversal.
Asíntotas
Son dos líneas rectas que se cruzan en el centro de la hipérbola. Las ramas de la hipérbola se acercan cada vez más a estas líneas a medida que se alejan del centro, pero nunca las tocan.
Vértices
Son los puntos donde la hipérbola "cambia de dirección" en cada una de sus ramas. Son los extremos del eje transversal.
Focos
Son dos puntos fijos (`F1` y `F2`) que son clave para definir la hipérbola. La diferencia de las distancias desde cualquier punto de la hipérbola a estos dos focos siempre es la misma.
Centro
Es el punto medio exacto entre los vértices y los focos de la hipérbola. Es el "corazón" de la figura.
Tangentes
Una línea tangente a una hipérbola en cualquier punto de la curva es una línea que toca la hipérbola en ese único punto.
¿Para qué se usa una Hipérbola?
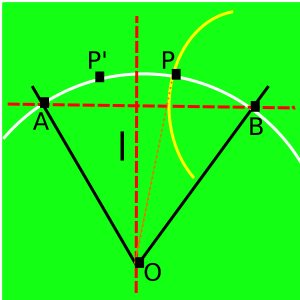
Trisección de un ángulo
El matemático Apolonio de Perge demostró que se puede usar una hipérbola para dividir un ángulo en tres partes iguales, un problema muy antiguo en geometría. Esto se logra dibujando un círculo y una hipérbola de una manera específica.
Otras curiosidades de las Hipérbolas
- Si "inviertes" una hipérbola especial (llamada hipérbola equilátera), obtienes otra curva interesante llamada lemniscata de Bernouilli.
- La lemniscata de Bernouilli es también la "podaria" de una hipérbola equilátera, lo que significa que están relacionadas de una forma geométrica particular.
Ver también
- Geometría analítica
- Sección cónica
- Recta
- Circunferencia
- Elipse
- Parábola
- Esferas de Dandelin
- Hipérbola unitaria
- Hiperbólico
Véase también
 En inglés: Hyperbola Facts for Kids
En inglés: Hyperbola Facts for Kids