Ecuación de Schrödinger para niños

La famosa ecuación de Schrödinger, creada por el físico austriaco Erwin Schrödinger en 1925 y publicada en 1926, nos ayuda a entender cómo se mueven las partículas muy pequeñas, como los electrones, en el mundo de la mecánica cuántica. Es como una regla fundamental para estas partículas, similar a cómo las leyes de Newton describen el movimiento de objetos más grandes en la mecánica clásica.

Esta ecuación es muy importante en la física, pero tiene sus límites. Por ejemplo, no se usa para describir situaciones donde las partículas se crean o desaparecen, como en la aniquilación de partículas. Para esos casos, se necesitan teorías más avanzadas.

¿Qué es la Ecuación de Schrödinger?

La Ecuación que Cambia con el Tiempo

La ecuación de Schrödinger tiene diferentes formas, dependiendo de lo que queramos describir. La más general nos muestra cómo un sistema cuántico evoluciona a medida que pasa el tiempo.

Una función de onda que se mueve libremente en el espacio. Este gráfico muestra la parte real de la función de onda.

Ecuación de Schrödinger dependiente del tiempo (general)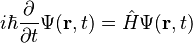

En esta ecuación, `i` es un número especial llamado unidad imaginaria, `ħ` es la "constante de Planck reducida" (un número muy pequeño pero importante en la física cuántica), y `Ψ` (la letra griega psi) es la función de onda del sistema. La función de onda es como un mapa que nos da información sobre la probabilidad de encontrar una partícula en un lugar y momento determinados. `Ĥ` es el operador Hamiltoniano, que representa la energía total del sistema.

Cada fila muestra una función de onda para un oscilador armónico cuántico. A la izquierda: la parte real (azul) y la parte imaginaria (roja). A la derecha: la probabilidad de encontrar la partícula. Las dos filas de arriba son estados estacionarios, como ondas que no se mueven. La fila de abajo no es estacionaria.

Un ejemplo común de esta ecuación es para una partícula simple que se mueve en un campo eléctrico:

Ecuación de Schrödinger dependiente del tiempo (partícula simple no relativista)

Aquí, `μ` es la masa de la partícula y `V` es su energía potencial. Esta parte de la ecuación nos dice que la energía total de la partícula es la suma de su energía cinética (energía de movimiento) y su energía potencial (energía almacenada).

La ecuación de Schrödinger es una ecuación diferencial en derivadas parciales lineal. Esto significa que es una ecuación matemática que describe cómo cambian las cosas en el espacio y el tiempo, y que sus soluciones se pueden combinar.

Para usar la ecuación de Schrödinger, primero se define la energía total del sistema (el Hamiltoniano) y luego se resuelve la ecuación para encontrar la función de onda. Esta función de onda nos da toda la información que necesitamos sobre el sistema.

La Ecuación para Estados Estables

La ecuación de Schrödinger también puede describir "estados estacionarios". Imagina una onda que no se mueve, como una onda estacionaria. Estos estados son muy importantes porque nos ayudan a entender el comportamiento de las partículas cuando su energía no cambia con el tiempo.

Ecuación de Schrödinger independiente del tiempo (general)

Esta ecuación nos dice que si el operador Hamiltoniano actúa sobre una función de onda `Ψ` y el resultado es la misma función de onda multiplicada por una constante `E`, entonces `Ψ` es un estado estacionario y `E` es la energía de ese estado.

Un ejemplo de esta ecuación para una partícula simple en un campo eléctrico es:

Ecuación de Schrödinger independiente del tiempo (partícula simple no relativista)

¿Cómo Nació la Ecuación?

Un Poco de Historia

A principios del siglo XX, los científicos descubrieron que la luz podía comportarse de dos maneras: como una onda electromagnética (por ejemplo, cuando se difracta) o como una partícula (llamada fotón, como en el efecto fotoeléctrico). Esto se conoce como la dualidad onda corpúsculo.

En 1923, un científico llamado Louis-Victor de Broglie propuso que esta idea de "onda y partícula" también se aplicaba a todas las demás partículas, como los electrones. Esto fue una idea muy novedosa en su momento. Más tarde, en 1927, se confirmó experimentalmente cuando se observó que los electrones también podían difractarse, como las ondas.

Esta idea de De Broglie inspiró a Schrödinger a buscar una ecuación que describiera estas "ondas" asociadas a las partículas. Quería una ecuación que, para objetos grandes, se pareciera a las leyes de la mecánica clásica.

El éxito de la ecuación de Schrödinger fue inmediato. Pudo explicar los niveles de energía de los electrones en el átomo de hidrógeno, lo que ayudó a entender por qué el hidrógeno emite luz en colores específicos (su espectro de emisión).

Al principio, algunos científicos famosos como Albert Einstein no estaban del todo de acuerdo con la interpretación de la función de onda que dio Max Born en 1926, porque introducía la idea de probabilidad en la física. Einstein decía que "Dios no juega a los dados".

El Camino de Schrödinger

Schrödinger se basó en una idea que ya había notado William Rowan Hamilton: existe una similitud entre cómo se mueven las ondas de luz y cómo se mueven las partículas en la mecánica clásica.

Schrödinger pensó: si la óptica (el estudio de la luz) tiene una ecuación de onda, ¿por qué la mecánica (el estudio del movimiento) no podría tener una? Así, buscó una ecuación de onda para las partículas que, al simplificarse, se pareciera a las ecuaciones de la mecánica clásica.

Curiosamente, Schrödinger primero intentó crear una ecuación para partículas que se movían a velocidades muy altas (relativistas), pero los resultados para el átomo de hidrógeno no coincidían con los experimentos. Por eso, se concentró en el caso de partículas que se mueven a velocidades más bajas (no relativistas), y ahí fue donde encontró el éxito.

¿Para Qué Sirve Resolver la Ecuación?

Resolver la ecuación de Schrödinger es como descifrar un código. Nos permite encontrar la función de onda, que contiene toda la información sobre el sistema cuántico.

Encontrar los Estados Propios

Los operadores en la ecuación de Schrödinger son "lineales". Esto significa que si varias funciones de onda son soluciones, cualquier combinación de ellas también lo será. Esto nos lleva a buscar soluciones especiales llamadas "estados propios" del Hamiltoniano. Estos estados, también conocidos como estados estacionarios, son muy importantes.

La ecuación que describe estos estados estacionarios se llama ecuación de Schrödinger independiente del tiempo. Nos ayuda a encontrar los niveles de energía que puede tener una partícula. Estos niveles de energía pueden ser discretos (como escalones, por ejemplo, en el átomo de hidrógeno) o continuos.

A veces, diferentes estados de una partícula pueden tener la misma energía. A esto se le llama "degeneración".

Una vez que conocemos estos estados propios y sus energías, podemos describir cualquier estado de un sistema como una combinación de ellos. La probabilidad de encontrar una partícula con una energía específica se calcula a partir de estos estados.

¿Es Fácil de Resolver?

En la mayoría de los casos, la ecuación de Schrödinger es muy difícil de resolver de forma exacta. Incluso para el átomo de hidrógeno, que es uno de los casos más simples, la solución exacta tiene limitaciones.

Sin embargo, hay algunos modelos sencillos que sí se pueden resolver y que son muy útiles para entender los principios de la mecánica cuántica. Algunos ejemplos son:

• Una partícula libre (sin fuerzas actuando sobre ella).
• Una partícula en una caja (confinada en un espacio pequeño).
• El oscilador armónico cuántico (una partícula que se mueve como un resorte).
• El átomo de hidrógeno.

Para los casos más complejos, los científicos usan métodos de aproximación o cálculos numéricos con computadoras.

La Ecuación de Schrödinger y el Mundo Clásico

La ecuación de Schrödinger es para el mundo cuántico, pero ¿qué pasa si la aplicamos a objetos grandes, como una pelota de fútbol? Resulta que, en el "límite clásico" (cuando los objetos son grandes y la constante de Planck es muy pequeña en comparación), la ecuación de Schrödinger se simplifica y se parece a las leyes de la mecánica clásica.

Esto explica por qué no vemos los efectos cuánticos en nuestra vida diaria. Para objetos grandes, los efectos cuánticos son tan pequeños que se vuelven insignificantes. Las partículas grandes se comportan como objetos localizados, y sus "ondas" se agrupan en lo que se llama un "paquete de ondas" que se mueve como una partícula clásica.

Más Allá de Schrödinger

Aunque la ecuación de Schrödinger es fundamental, tiene algunas limitaciones:

• No es "relativista", lo que significa que no es precisa para partículas que se mueven a velocidades cercanas a la velocidad de la luz. Para eso, se necesitan ecuaciones como la ecuación de Dirac o la ecuación de Klein-Gordon.
• No describe correctamente una propiedad de las partículas llamada "espín". Para incluir el espín, se usa una versión modificada llamada ecuación de Pauli. Más tarde, Paul Dirac creó la ecuación de Dirac, que sí incluye el espín y los efectos relativistas.

Galería de imágenes

• 

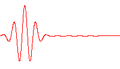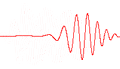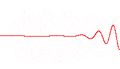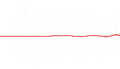
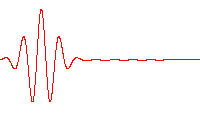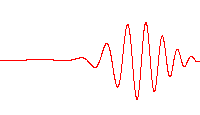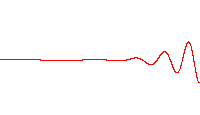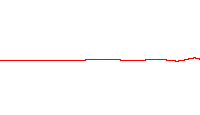
  Una función de onda que satisface la ecuación no relativista de Schrödinger con V Plantilla:= 0. Es decir, corresponde a una partícula viajando libremente a través del espacio libre. Este gráfico es la parte real de la función de onda.

• 

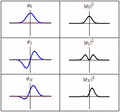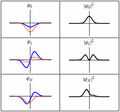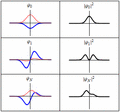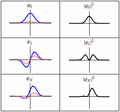
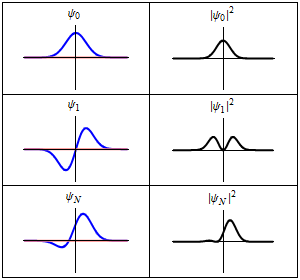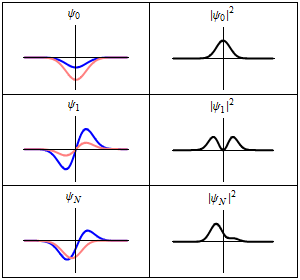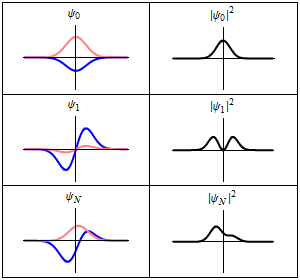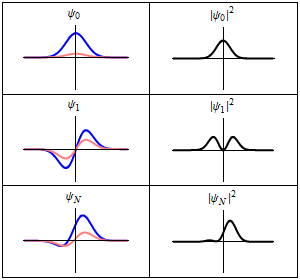
  Cada una de las tres filas es una función de onda que satisfacen la ecuación de Schrödinger dependiente del tiempo para un oscilador armónico cuántico. A la izquierda: La parte real (azul) y la parte imaginaria (rojo) de la función de onda. A la derecha: La distribución de probabilidad de hallar una partícula con esta función de onda en una posición determinada. Las dos filas de arriba son ejemplos de estados estacionarios, que corresponden a ondas estacionarias. La fila de abajo es un ejemplo de un estado que no es estacionario. La columna de la derecha ilustra por qué el estado puede llamarse "estacionario".

Véase también

En inglés: Schrödinger equation Facts for Kids