Mecánica de fluidos para niños
La mecánica de fluidos es una parte de la física que se encarga de estudiar cómo se mueven los fluidos, como el agua o el aire, y las fuerzas que hacen que se muevan. Los fluidos tienen una característica especial: no tienen una forma fija y se adaptan al recipiente que los contiene. Esto se debe a que no pueden resistir ciertas fuerzas que intentarían cambiar su forma. También estudia cómo interactúan los fluidos con los objetos o los límites que los rodean.
Esta área de estudio se divide en dos partes principales:
- Estática de fluidos: Se enfoca en los fluidos que están en reposo, es decir, sin moverse.
- Dinámica de fluidos: Estudia cómo las fuerzas afectan el movimiento de los fluidos.
La mecánica de fluidos ve la materia de forma "macroscópica", es decir, como un todo continuo, sin fijarse en los átomos individuales. Es un campo de investigación muy activo y a veces complejo. Muchos problemas se resuelven usando métodos numéricos con computadoras, una técnica conocida como dinámica de fluidos computacional (CFD). También se usan métodos experimentales, como la Velocimetría de imágenes de partículas, para ver y analizar cómo fluyen los fluidos.
Es importante saber que los gases se pueden comprimir (su volumen puede cambiar), mientras que los líquidos casi no se comprimen, aunque sí toman la forma del recipiente.
Contenido
Historia de la Mecánica de Fluidos
La historia de la mecánica de fluidos nos muestra cómo el conocimiento sobre los fluidos ha evolucionado desde la antigüedad. Mucho antes de que se estudiara de forma científica, la gente ya usaba los principios de los fluidos en su vida diaria.
Primeros Usos y Descubrimientos
Desde hace miles de años, los humanos han controlado el agua para la agricultura y la construcción. Ya en el año 6500 a.C., se usaba el riego a pequeña escala. Hacia el 3000 a.C., se construían grandes obras hidráulicas como canales y presas en lugares como los ríos Nilo y Amarillo. Los acueductos más antiguos podrían haberse construido en Creta y Palestina.
El estudio teórico de los fluidos comenzó más tarde. En el siglo III a.C., en Alejandría, Arquímedes formuló el famoso principio de Arquímedes, que explica por qué los objetos flotan o se hunden. En el siglo I, Heron de Alejandría continuó estos estudios, descubriendo principios sobre la presión y el caudal (la cantidad de fluido que pasa por un lugar en un tiempo).
Durante la Antigüedad tardía, se siguieron construyendo grandes obras hidráulicas como acueductos y sistemas de distribución de agua. En la Edad Media, aunque algunos conocimientos se perdieron en Europa, se conservaron y desarrollaron en el mundo islámico. También en China, en el siglo VII, se inició la construcción del Gran Canal de China.
Grandes Pensadores y Avances
En el siglo XV, Leonardo da Vinci retomó el estudio de los fluidos. Describió diferentes tipos de flujo y formuló el principio de continuidad, que dice que la masa de un fluido se conserva. Él sentó las bases de la hidrodinámica y diseñó inventos como el paracaídas y la bomba centrífuga.
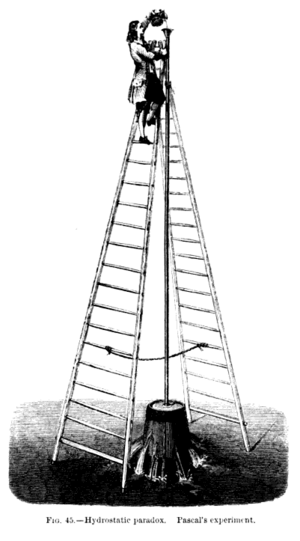
Más tarde, Simon Stevin y Blaise Pascal hicieron importantes descubrimientos sobre la hidrostática (fluidos en reposo). Pascal, en 1648, presentó de forma clara los principios fundamentales de la hidrostática, incluyendo la "paradoja hidrostática", que se demuestra con experimentos como el del barril de Pascal.
En el siglo XVII, Isaac Newton también contribuyó al estudio de los fluidos. Pero fue con la llegada de las matemáticas avanzadas que la mecánica de fluidos ganó mucha profundidad. En 1738, Daniel Bernoulli estableció leyes para fluidos sin viscosidad usando el principio de conservación de la energía.
Jean le Rond D'Alembert y Leonhard Euler desarrollaron las ecuaciones que describen el movimiento de los fluidos. En 1755, Euler publicó ecuaciones diferenciales parciales para fluidos incompresibles perfectos. Sin embargo, D'Alembert notó una "paradoja" donde la teoría no coincidía con la realidad. Esta paradoja fue resuelta por Henri Navier en 1820 y George Gabriel Stokes en 1845, quienes introdujeron el concepto de fricción (viscosidad) en las ecuaciones. Las ecuaciones de Navier-Stokes son fundamentales desde entonces.
La Mecánica de Fluidos Moderna
En los siglos XIX y XX, la mecánica de fluidos siguió evolucionando. Se desarrollaron conceptos como la capa límite por Ludwig Prandtl, muy importante para la aerodinámica y la hidrodinámica naval. También se estudiaron los flujos supersónicos y los flujos en medios porosos.
Un campo de estudio muy activo es la turbulencia, que aún no se comprende completamente. Científicos como Ludwig Boltzmann y Andréi Kolmogórov hicieron grandes avances en la descripción estadística de los gases y la turbulencia.
El desarrollo de computadoras potentes en la segunda mitad del siglo XX dio origen a la mecánica de fluidos computacional (CFD). Esta rama permite realizar "experimentos numéricos" que simulan el comportamiento de los fluidos, ayudando a entender fenómenos complejos como la turbulencia.
Hoy en día, la mecánica de fluidos es crucial en muchos campos industriales y científicos, como la meteorología, la climatología, la oceanografía y la astrofísica.
Ideas Básicas de la Mecánica de Fluidos
En la mecánica de fluidos, se usan algunas ideas fundamentales para entender cómo se comportan los fluidos. Se asume que los fluidos siguen leyes importantes como:
- La masa y el movimiento se conservan.
- Las leyes de la termodinámica (que tratan sobre la energía y el calor).
Hipótesis del Medio Continuo
Esta es una idea clave. Imagina que el fluido es como una sustancia continua que llena todo el espacio, sin huecos. No nos fijamos en que está hecho de moléculas separadas. Así, podemos decir que propiedades como la densidad o la temperatura cambian de forma suave y continua en el fluido.
Para saber si esta idea es válida, comparamos el tamaño de las moléculas con el tamaño del sistema que estamos estudiando. Si las moléculas son muy pequeñas comparadas con el sistema, entonces podemos considerar el fluido como un medio continuo. Si no, hay que usar otras formas de estudio.
Concepto de Partícula Fluida
Este concepto está relacionado con el anterior. Una "partícula fluida" es como un trocito muy pequeño de fluido que está en un punto del espacio en un momento dado. Este trocito es lo suficientemente grande como para tener muchas moléculas, pero lo suficientemente pequeño como para que sus propiedades (como la densidad) sean las mismas en todo su interior.
Es importante recordar que esta partícula fluida se mueve con el fluido. Así, un punto en el espacio puede ser ocupado por diferentes partículas fluidas en distintos momentos.
Cómo Describir el Movimiento de un Fluido
Hay dos maneras principales de describir cómo se mueve un fluido:
- Descripción Lagrangiana: Es como seguir a cada "partícula fluida" individualmente. Imagina que le pones una etiqueta a cada partícula y sigues su camino, anotando su posición y propiedades en cada momento.
- Descripción Euleriana: En lugar de seguir partículas, te fijas en puntos fijos en el espacio. En cada punto, mides las propiedades del fluido (velocidad, presión, etc.) que pasa por allí en ese instante, sin importar qué partícula fluida lo esté ocupando.
La descripción euleriana es la más usada porque es más práctica para la mayoría de los problemas.
Ecuaciones Clave de la Mecánica de Fluidos
Las ecuaciones que rigen la mecánica de fluidos se basan en los principios de conservación de la mecánica y la termodinámica. Se usan herramientas matemáticas como el teorema del transporte de Reynolds para obtenerlas.
Las tres ecuaciones fundamentales son:
- La ecuación de continuidad (conservación de la masa).
- La ecuación de la cantidad de movimiento (relacionada con las fuerzas y el movimiento).
- La ecuación de la conservación de la energía.
Estas ecuaciones, en su forma diferencial, se conocen como ecuaciones de Navier-Stokes. Si el fluido no tiene viscosidad, se simplifican a las ecuaciones de Euler.
Resolver estas ecuaciones es muy complejo, por lo que a menudo se simplifican para problemas específicos o se usan soluciones numéricas con computadoras, lo que se conoce como mecánica de fluidos computacional.
Ecuación de Continuidad
Esta ecuación expresa que la masa de un fluido se conserva. En términos sencillos, dice que el fluido no aparece ni desaparece. Si el fluido es incompresible (su densidad no cambia), significa que la cantidad de fluido que entra en un lugar debe ser igual a la que sale.
- Forma integral:
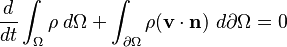
- Forma diferencial:
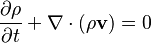
Ecuación de Cantidad de Movimiento
Esta ecuación es como la Segunda Ley de Newton (fuerza = masa x aceleración) aplicada a un fluido. Dice que los cambios en el movimiento de un trozo de fluido son causados por las fuerzas que actúan sobre él, como la presión del fluido, las fuerzas de viscosidad (fricción interna) y la gravedad.
- Forma integral:
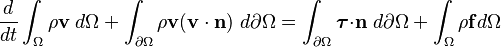
- Forma diferencial:
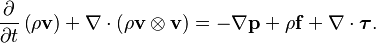
Ecuación de la Conservación de Energía
Esta ecuación establece que la energía total de un fluido se conserva. Considera la energía interna del fluido, su energía de movimiento y cómo la energía se transfiere por calor o por el trabajo de las fuerzas.
- Forma integral:
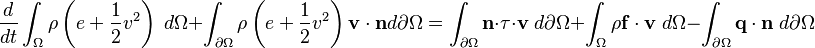
- Forma diferencial:
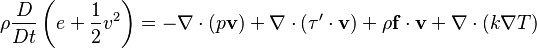
Fluidos sin Viscosidad y Fluidos Viscosos
Un fluido sin viscosidad es una idea teórica donde el fluido no tiene ninguna "fricción interna". En la vida real, casi todos los fluidos son viscosos, lo que significa que tienen cierta resistencia a fluir. La viscosidad es muy importante cerca de las superficies sólidas, donde el fluido se "pega" a la superficie.
A veces, para simplificar los cálculos, se asume que el fluido es sin viscosidad fuera de una zona muy delgada cerca de la superficie, llamada capa límite.
Dinámica de los Fluidos
La fluidodinámica es la parte de la mecánica de fluidos que estudia los líquidos y gases en movimiento. Nos ayuda a entender y predecir cómo se comportan los fluidos en muchas situaciones prácticas. Al resolver un problema de fluidodinámica, se calculan propiedades como la velocidad, la presión, la densidad y la temperatura del fluido en diferentes puntos y momentos.
Tiene varias ramas, como la aerodinámica (el estudio del aire y otros gases en movimiento, importante para aviones) y la hidrodinámica (el estudio de los líquidos en movimiento, útil para barcos o tuberías).
La dinámica de fluidos se usa en muchas áreas, como:
- Calcular las fuerzas en aviones.
- Determinar cuánto petróleo fluye por un oleoducto.
- Predecir el clima.
- Entender las nebulosas en el espacio interestelar.
- Modelar explosiones.
- Incluso en la ingeniería del tráfico para entender el flujo de vehículos.
|
Véase también
 En inglés: Fluid mechanics Facts for Kids
En inglés: Fluid mechanics Facts for Kids
|
|
|
|