Congruencia (teoría de números) para niños

La congruencia es un concepto muy útil en la teoría de números, una rama de las matemáticas. Nos ayuda a entender cómo se relacionan los números enteros cuando los dividimos.

Imagina que tienes dos números enteros, por ejemplo, 17 y 5. Si los divides por 3, ¿qué resto obtienes?

• 17 dividido por 3 es 5 y el resto es 2.
• 5 dividido por 3 es 1 y el resto es 2.

Como ambos números (17 y 5) tienen el mismo resto (2) al dividirlos por 3, decimos que 17 y 5 son congruentes módulo 3.

Esto se escribe de una forma especial:

17 5 (mod 3)

Se lee: "17 es congruente con 5 módulo 3". El número 3 es el módulo.

En general, dos números enteros, digamos a y b, son congruentes módulo m (donde m es un número natural distinto de cero) si:

• El número m divide exactamente la diferencia entre a y b. Es decir, si restas b de a (a - b), el resultado se puede dividir por m sin dejar resto.
• O, lo que es lo mismo, a y b dejan el mismo resto cuando los divides por m.
• También significa que puedes escribir a como la suma de b y un múltiplo de m. Por ejemplo, si 17 5 (mod 3), entonces 17 = 5 + (4 * 3), donde 4 es un número entero.

La idea de congruencia se usa de dos maneras principales:

• Como una identidad matemática: A veces, una congruencia es una verdad que siempre se cumple. Por ejemplo, el pequeño teorema de Fermat dice que para cualquier número primo p y cualquier número entero a que no sea divisible por p, siempre se cumple que:

 :a^p-1 1 (mod p). Esto es como una regla general que siempre funciona.

• Como una ecuación: Otras veces, la congruencia es como un problema o una ecuación donde hay una o más incógnitas (números que no conocemos) y queremos encontrar sus valores. Por ejemplo, si tenemos la congruencia:

 :x² - 5 0 (mod 11) Aquí, queremos saber qué valores de x hacen que esta afirmación sea cierta. En este caso, las soluciones son los números x que son congruentes con 4 módulo 11 (como 4, 15, 26...) o con 7 módulo 11 (como 7, 18, 29...). Esto significa que si sustituyes x por 4 o 7 (o cualquier número que deje el mismo resto que 4 o 7 al dividirlo por 11), la congruencia se cumple.

¿Quién inventó la Congruencia?

La notación y el concepto de congruencia fueron presentados por el famoso matemático Carl Friedrich Gauss en su libro Disquisitiones Arithmeticae en el año 1801. Desde entonces, se ha usado en muchos otros campos donde se habla de divisibilidad, como en el estudio de polinomios o en la teoría de anillos.

Propiedades de la Congruencia

La relación de congruencia comparte muchas características con la igualdad matemática. Aquí te mostramos algunas de sus propiedades más importantes:

• Simetría: Si a es congruente con b módulo m (a b (mod m)), entonces b también es congruente con a módulo m (b a (mod m)).
• Transitividad: Si a es congruente con b módulo m (a b (mod m)) y b es congruente con c módulo m (b c (mod m)), entonces a también es congruente con c módulo m (a c (mod m)).

• Si a no tiene factores comunes con m (aparte del 1) y a es congruente con b módulo m, entonces b tampoco tendrá factores comunes con m.

• Si a es congruente con b módulo m (a b (mod m)) y k es cualquier número entero, entonces también se cumple:

* Puedes sumar o restar k a ambos lados: a 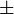k b 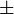k (mod m) * Puedes multiplicar ambos lados por k: ka kb (mod m) * Puedes elevar ambos lados a una potencia k (si k es mayor que 0): a^k b^k (mod m)

• Si k no tiene factores comunes con m (aparte del 1), entonces podemos "dividir" ambos lados de la congruencia por k. Esto significa que si a b (mod m), entonces:

 :a/k b/k (mod m) (Aquí, "dividir" significa multiplicar por el inverso de k en el sistema modular).

• Como resultado de todo lo anterior, si tenemos dos congruencias con el mismo módulo:

 :a b (mod m) y c d (mod m) Podemos sumarlas, restarlas o multiplicarlas, y las nuevas congruencias también serán válidas:  :a + c b + d (mod m)  :ac bd (mod m)

Véase también

• Aritmética modular