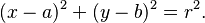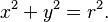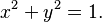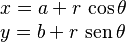Circunferencia para niños

No debe confundirse con Círculo.

Circunferencia con centro en el punto M y radio r

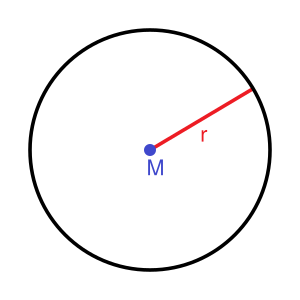
La circunferencia es una línea curva y cerrada. Todos sus puntos están a la misma distancia de un punto central.

Imagina que dibujas un círculo perfecto con un compás. La línea que trazas es la circunferencia. Está formada por infinitos puntos en un plano que se encuentran a una distancia fija de un punto llamado centro. Esa distancia fija se llama radio.

Una circunferencia es el lugar geométrico de los puntos de un plano que están a la misma distancia de otro punto llamado centro.

Es importante no confundir la circunferencia con el círculo. La circunferencia es solo la línea curva, el "borde". El círculo es toda la superficie plana que está dentro de esa circunferencia.

Circunferencias que aparecen al cortar una esfera con un plano de diferentes maneras.

¿De dónde viene la circunferencia?

Origen e historia de la circunferencia

El interés por entender y usar la circunferencia comenzó hace mucho tiempo, en lugares como la antigua Babilonia. La gente necesitaba saber cómo medir y trabajar con las ruedas de los carros. Era muy importante relacionar el tamaño de la rueda (su diámetro o radio) con la distancia que recorría al girar (la longitud de su circunferencia). Esto ayudó a fabricar ruedas más precisas y a mejorar el transporte.

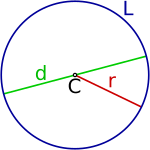
Partes de una circunferencia

Para entender bien una circunferencia, es útil conocer sus partes principales:

El centro: Es el punto que está exactamente en medio de la circunferencia. Todos los puntos de la circunferencia están a la misma distancia de él. En los dibujos, se suele representar con la letra $C$ .
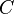El radio: Es un segmento de línea que va desde el centro hasta cualquier punto de la circunferencia. También se usa la palabra "radio" para referirse a la longitud de ese segmento. Se representa con la letra $r$ .
El diámetro: Es un segmento de línea que une dos puntos de la circunferencia y que siempre pasa por el centro. El diámetro es el doble de largo que el radio (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): d = 2 \cdot r ). Se representa con la letra $d$ .
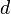El perímetro: Es la longitud total de la línea de la circunferencia, es decir, cuánto mide su contorno. Se representa con la letra $L$ .

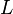Una cuerda: Es un segmento de línea que une dos puntos cualquiera de la circunferencia, sin necesidad de pasar por el centro. El diámetro es la cuerda más larga que puede tener una circunferencia.
Un arco: Es una porción o parte de la circunferencia que está entre dos puntos.
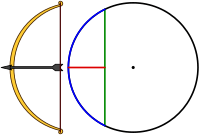
Una flecha o sagita: Es un segmento que va desde el punto medio de una cuerda hasta el arco que esa cuerda "corta", sin pasar por el centro.
Una semicircunferencia: Es la mitad de una circunferencia, delimitada por los extremos de un diámetro.

¿Cómo se calcula el perímetro de una circunferencia?

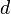La longitud del perímetro de una circunferencia se calcula usando el radio ( $r$ ) o el diámetro ( $d$ ) y un número muy especial llamado pi ( $\pi$ ).

La fórmula es:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \ell=2\pi\cdot r

O también:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \ell=\pi\cdot d

Donde $\pi$ (pi) es un número constante que vale aproximadamente 3.14159.

¿Cómo se calcula el área de un círculo?

Aunque este artículo es sobre la circunferencia, es importante saber que el área de la superficie que encierra (el círculo) se calcula así:

A = Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \pi\cdot r^2

O también:

A =

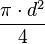
\frac{\pi\cdot d^2}{4}

Posiciones de puntos y líneas respecto a una circunferencia

Podemos describir cómo se relacionan los puntos y las líneas con una circunferencia.

Puntos y la circunferencia

Posiciones de un punto respecto a una circunferencia.

Un punto exterior: Está fuera de la circunferencia, a una distancia mayor que el radio desde el centro.
Un punto interior: Está dentro de la circunferencia, a una distancia menor que el radio desde el centro.
Un punto sobre la circunferencia: Está exactamente en la línea de la circunferencia, a una distancia igual al radio desde el centro.

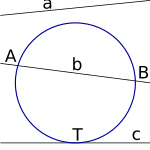
Líneas y la circunferencia

Posiciones de las rectas respecto a una circunferencia.

Una recta exterior: Es una línea que no toca la circunferencia en ningún punto.
Una recta tangente: Es una línea que toca la circunferencia en un solo punto. Ese punto se llama punto de tangencia.
Una recta secante: Es una línea que corta la circunferencia en dos puntos diferentes.

Una propiedad importante es que cualquier recta tangente a una circunferencia siempre forma un ángulo recto (90 grados) con el radio que llega al punto de tangencia.

Relación entre dos circunferencias

Posiciones relativas entre dos circunferencias.

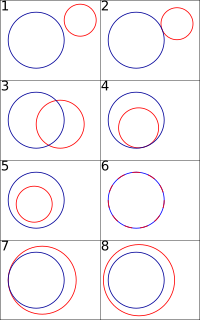
Dos circunferencias pueden estar en diferentes posiciones entre sí:

Exteriores: No se tocan en ningún punto y una está completamente fuera de la otra. (Figuras 1 y 8)
Interiores: Una está completamente dentro de la otra y no se tocan. (Figura 5)
Tangentes exteriores: Se tocan en un solo punto y una está fuera de la otra. (Figura 2)
Tangentes interiores: Se tocan en un solo punto y una está dentro de la otra. (Figura 4)
Secantes: Se cortan en dos puntos diferentes. (Figura 3)
Concéntricas: Tienen el mismo centro, pero radios diferentes. (Figura 6, si una fuera más pequeña)
Coincidentes: Tienen el mismo centro y el mismo radio, son exactamente la misma circunferencia. (Figura 6)

Una propiedad interesante es que si dos circunferencias son tangentes (se tocan en un punto), sus centros y el punto de tangencia siempre están en la misma línea recta.

Ángulos en una circunferencia

Tipos de ángulos en una circunferencia.

Los ángulos que se forman con una circunferencia tienen nombres especiales:

Un ángulo central: Su vértice (la esquina del ángulo) está en el centro de la circunferencia. (Figura 1)
Un ángulo inscrito: Su vértice está sobre la circunferencia, y sus lados cortan la circunferencia en dos puntos. (Figura 2)
Un ángulo semiinscrito: Su vértice está sobre la circunferencia, uno de sus lados es una cuerda y el otro es una recta tangente a la circunferencia en ese vértice. (Figura 3)
Un ángulo interior: Su vértice está dentro de la circunferencia, pero no en el centro. (Figura 5)
Un ángulo exterior: Su vértice está fuera de la circunferencia, y sus lados son tangentes o secantes a la circunferencia. (Figuras 6, 7 y 8)

Circunferencias y polígonos

Inscripción y circunscripción

Una circunferencia está circunscrita a un polígono cuando todos los vértices del polígono tocan la circunferencia. Se dice que el polígono está inscrito en la circunferencia.
Una circunferencia está inscrita en un polígono cuando es tangente (toca en un solo punto) a todos los lados del polígono. Se dice que el polígono está circunscrito a la circunferencia.

¿Cómo dibujar una circunferencia con regla y compás?

Puedes dibujar una circunferencia de varias maneras usando solo una regla y un compás.

Conociendo el centro y un punto de la circunferencia

Esta es la forma más fácil:

Coloca la punta del compás en el centro de la circunferencia.
Abre el compás hasta el punto que sabes que está en la circunferencia.
Gira el compás para trazar la línea.

Conociendo el diámetro

Encuentra el punto medio del diámetro. Ese será el centro de la circunferencia.
Luego, usa el método anterior: coloca la punta del compás en el centro y ábrelo hasta uno de los extremos del diámetro.

Construcción de una circunferencia que pasa por tres puntos (A, B, C) encontrando las mediatrices (rojo) de los lados del triángulo (azul). El punto donde se cruzan las mediatrices es el centro de la circunferencia.

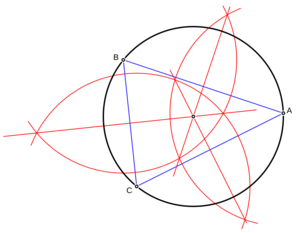
Conociendo tres puntos que no están en línea recta

Si tienes tres puntos que no forman una línea recta, siempre puedes dibujar una única circunferencia que pase por ellos:

Llama a los puntos A, B y C.
Dibuja los segmentos de línea AB y BC.
Dibuja la mediatriz (una línea que corta un segmento justo por la mitad y forma un ángulo recto con él) del segmento AB.
Dibuja la mediatriz del segmento BC.
El punto donde se cruzan estas dos mediatrices es el centro de la circunferencia. Llama a este punto M.
Ahora, con el centro M y cualquiera de los tres puntos (A, B o C) como referencia para el radio, puedes dibujar la circunferencia.

Representación de la circunferencia con ecuaciones

En matemáticas, podemos describir una circunferencia usando ecuaciones. Estas ecuaciones nos dicen dónde están todos los puntos de la circunferencia en un sistema de coordenadas.

Ecuación de la circunferencia

Archivo:Cartesian-coordinate-system-with-circle

Circunferencia de radio dos en un sistema de coordenadas.

Si el centro de la circunferencia está en un punto 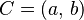$C=(a,\,b)$ y tiene un radio $r$ , su ecuación es:

(x-a)^2 + (y-b)^2 = r^2.

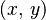Aquí, $(x,\,y)$ representa cualquier punto de la circunferencia.

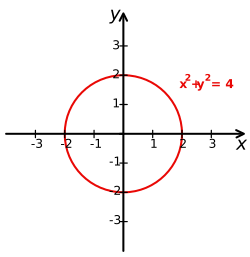
Si la circunferencia está centrada en el origen de las coordenadas (el punto Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (0,\,0) ), la ecuación se simplifica a:

x^2 + y^2 = r^2.

La circunferencia que tiene su centro en el origen y un radio de 1 se llama circunferencia unidad o circunferencia goniométrica. Su ecuación es:

x^2 + y^2 = 1.

Función paramétrica

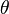También podemos describir una circunferencia usando funciones paramétricas. Esto significa que las coordenadas $x$ e $y$ de cada punto de la circunferencia se expresan en función de un solo parámetro, generalmente un ángulo $\theta$ .

Para una circunferencia con centro en 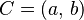$C=(a,\,b)$ y radio $r$ , las ecuaciones paramétricas son:

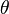\begin{array}{l} x= a + r\,\cos \theta \\ y= b + r\,\sen \theta \end{array}

Donde $\theta$ es el ángulo que va desde 0 hasta casi 360 grados (o 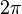$2\pi$ radianes).

Circunferencias especiales

Algunas circunferencias tienen nombres particulares por sus propiedades o por cómo se usan:

Circunferencias de Cardanus: Son un par de circunferencias que se mueven una sobre la otra, tocándose por dentro, y una tiene el doble de tamaño que la otra. Fueron estudiadas por el matemático Girolamo Cardano.
Circunferencia osculatriz: Se usa para describir la curvatura de una línea o superficie en un punto específico. Es la circunferencia que mejor se "ajusta" a la curva en ese punto.

Ver también

Véase también

En inglés: Circumference Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Circunferencia&oldid=4840337»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Circunferencia para Niños. Enciclopedia Kiddle.