Trapecio (geometría) para niños
Datos para niños Trapecio |
||
|---|---|---|
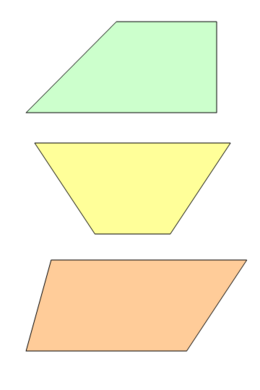 4 lados con solo dos paralelos
(Trapecios rectángulo, isósceles y escaleno) |
||
| Características | ||
| Tipo | Cuadrilátero, no paralelogramo | |
| Lados | 4 | |
| Vértices | 4 | |
| Grupo de simetría | m | |
| Polígono dual | Rectángulo | |
| Propiedades | ||
| Convexo, cíclico Ángulos opuestos y lados cogruentes. |
||
En geometría, un trapecio es una figura con cuatro lados (un cuadrilátero). Lo especial de un trapecio es que tiene solo un par de lados paralelos.
Los lados paralelos de un trapecio se llaman bases. Los otros dos lados, que no son paralelos, se conocen como lados laterales o catetos. Un trapecio es siempre una figura convexa, lo que significa que todos sus ángulos internos son menores de 180 grados.
Contenido
¿Qué es un Trapecio?
Un trapecio es un tipo de cuadrilátero. Se diferencia de otras figuras de cuatro lados, como los paralelogramos, porque solo tiene un par de lados que nunca se cruzan, es decir, son paralelos.
En matemáticas, a veces se discute si un paralelogramo (que tiene dos pares de lados paralelos) puede ser considerado un trapecio. En este artículo, consideramos que sí, que un paralelogramo es un tipo especial de trapecio. Esto es común en matemáticas más avanzadas.
Origen del Nombre
La palabra "trapecio" viene del griego antiguo "trapezia", que significa "una mesa". Esto se debe a la forma que a menudo tienen estas figuras. A lo largo de la historia, ha habido algunas diferencias en cómo se usan los términos "trapecio" y "trapezoide" en diferentes idiomas, especialmente entre el inglés británico y el americano. Sin embargo, en español, la definición de trapecio es clara: un cuadrilátero con un solo par de lados paralelos.
Partes Importantes de un Trapecio
Para entender bien un trapecio, es útil conocer sus partes principales:
- Bases: Son los dos lados paralelos del trapecio. Uno suele ser más largo que el otro.
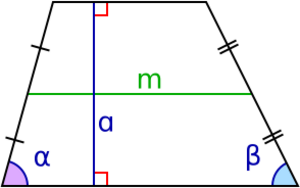
- Altura: Es la distancia perpendicular entre las dos bases. Imagina una línea recta que va de una base a la otra formando un ángulo de 90 grados. Esa es la altura. Se representa con la letra h.
- Mediana: Es un segmento que une los puntos medios de los lados no paralelos. Su longitud es igual a la suma de las bases dividida entre dos. Se representa con la letra m.
* La fórmula para la mediana es: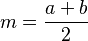 
, donde a y b son las longitudes de las bases.
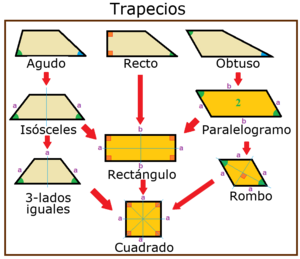
Tipos de Trapecios
Los trapecios se clasifican según sus ángulos y la longitud de sus lados no paralelos:
Trapecio Rectángulo
- Un trapecio rectángulo tiene al menos un lado lateral que es perpendicular a las bases.
- Esto significa que tiene dos ángulos rectos (de 90 grados) adyacentes.
Trapecio Isósceles
- Un trapecio isósceles tiene sus dos lados no paralelos de la misma longitud.
- Sus ángulos en la base son iguales. Por ejemplo, los dos ángulos de abajo son iguales, y los dos ángulos de arriba también son iguales.
- Tiene un eje de simetría que lo divide en dos partes iguales.
- Las diagonales de un trapecio isósceles también son de la misma longitud.
Trapecio Escaleno
- Un trapecio escaleno es el que no es ni rectángulo ni isósceles.
- Todos sus lados no paralelos tienen longitudes diferentes.
- Todos sus cuatro ángulos internos son diferentes entre sí.
Paralelogramo
- Un paralelogramo es un caso especial de trapecio que tiene dos pares de lados paralelos.
- Esto significa que los lados opuestos son paralelos y de la misma longitud.
- Los rectángulos y los cuadrados son tipos de paralelogramos, y por lo tanto, también son trapecios.
¿Cómo Calcular el Área de un Trapecio?
El área de un trapecio es el espacio que ocupa en una superficie plana. Para calcularla, necesitas conocer la longitud de sus dos bases y su altura.
- La fórmula para el área A de un trapecio es:
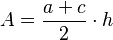Donde: * a es la longitud de una base. * c es la longitud de la otra base. * h es la altura del trapecio.
Esta fórmula significa que sumas las longitudes de las dos bases, divides el resultado entre dos (esto te da el promedio de las bases), y luego multiplicas por la altura.
Aplicaciones del Trapecio en la Vida Real
Los trapecios no son solo figuras de libros de matemáticas; los vemos en muchos lugares:
En la Arquitectura
- En la arquitectura, especialmente en estilos antiguos como el egipcio o el incaico, se usaban formas trapezoidales para puertas, ventanas y edificios. Estas estructuras son más anchas en la base y se estrechan hacia arriba, dándoles una apariencia única y estable.
En la Biología
- En la biología, los científicos usan términos como "trapezoidal" o "trapeziforme" para describir la forma de órganos o partes del cuerpo de animales y plantas. Por ejemplo, la forma de algunas partes de insectos puede ser trapezoidal.
Galería de imágenes
-
"Trapecio" y "Trapezoide": error de Hutton (1795)
-
Trapecio isósceles
-
Trapecio escaleno
-
Cuadrilátero irregular
-
Rombo
-
Romboide
-
El Templo de Dendur en el Museo Metropolitano de Arte en Nueva York
-
Ejemplo de un protórax trapeciforme esbozado en un hemíptero
-
Mediana de un trapecio
-
Tipos de trapecios: 1. Rectángulo, 2. Isósceles, 3 y 4. Escalenos
.png){kind=small}
.png)
.png)
.png)
.png)
Véase también
En inglés: Trapezoid Facts for Kids
