Plano (geometría) para niños
En geometría, un plano es una superficie ideal que solo tiene dos dimensiones. Imagina una hoja de papel que se extiende infinitamente en todas direcciones, sin grosor. Un plano contiene infinitos puntos y rectas. Es uno de los conceptos más importantes en geometría, junto con el punto y la recta.
Una recta que está dentro de un plano lo divide en dos partes, llamadas semiplanos. La recta que los separa se conoce como la frontera o el borde de esos semiplanos.
Cuando hablamos de "un plano" en geometría, nos referimos a esta superficie bidimensional sin volumen, llena de puntos y rectas. Pero si usamos la palabra "planos" en plural, a menudo nos referimos a dibujos o representaciones gráficas de superficies. Los planos son muy útiles en ingeniería, arquitectura y diseño. Se usan para dibujar ideas en una superficie plana antes de construir algo en tres dimensiones.
Contenido
¿Cómo se define un plano?
Un plano puede quedar completamente definido si conocemos algunos elementos geométricos específicos:
- Tres puntos que no estén en la misma línea recta.
- Una recta y un punto que no esté sobre esa recta.
- Dos rectas que sean paralelas o dos rectas que se crucen en un punto.
Los planos suelen nombrarse con letras del alfabeto griego, como alfa (α), beta (β) o gamma (γ). Para dibujarlos, se representan como una figura con bordes irregulares. Esto nos ayuda a recordar que, aunque el dibujo es limitado, el plano real se extiende sin fin.
Puntos en un plano: Coordenadas
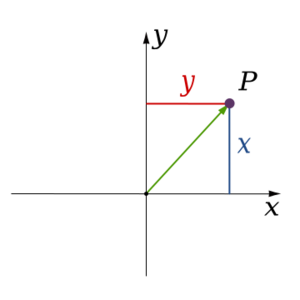
En un sistema de coordenadas cartesianas, la posición de un punto en un plano se describe con un par ordenado de números. Estos números se llaman abscisa (el valor en el eje horizontal) y ordenada (el valor en el eje vertical). Así, cada punto tiene un par de números únicos, y cada par de números representa un punto único en el plano. Este sistema es la base de la geometría analítica, que conecta la geometría con el álgebra.
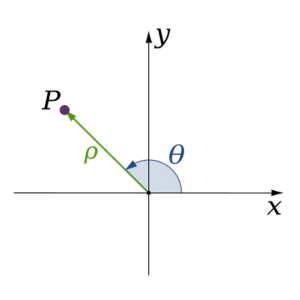
También existen las coordenadas polares, donde un punto se describe por su distancia desde un punto central y el ángulo que forma con una línea de referencia.
¿Qué es el área de una superficie plana?
El área es una medida que nos dice cuánto espacio ocupa una superficie o una figura geométrica plana. Se mide en unidades de medida especiales, como metros cuadrados (m²) o centímetros cuadrados (cm²). Para figuras planas con lados rectos, como un polígono, podemos dividirla en triángulos y sumar las áreas de cada triángulo para encontrar el área total. A veces, la palabra "área" se usa como sinónimo de "superficie", pero es importante recordar que el área es la medida y la superficie es el objeto geométrico.
Historia del concepto de plano
El estudio de los planos tiene una larga historia. Los primeros libros de los Elementos de Euclides, escritos por el matemático griego Euclides, ya hablaban de la geometría bidimensional. En ellos se explicaban ideas como la semejanza de formas, el famoso teorema de Pitágoras, la igualdad de ángulos y áreas, y el paralelismo.
Más tarde, en el siglo XVII, el filósofo y matemático René Descartes y, de forma independiente, Pierre de Fermat, desarrollaron el sistema de coordenadas cartesianas. Este sistema revolucionó la geometría al permitir describir puntos en un plano usando pares de números. Al principio, usaban un solo eje, pero la idea de usar dos ejes perpendiculares (el eje 'x' y el eje 'y') se popularizó después de que los escritos de Descartes fueran traducidos al latín. El punto donde se cruzan estos ejes se llama origen, y sus coordenadas son (0, 0).
El plano en la geometría
Sistemas de coordenadas
En matemáticas, la geometría analítica nos permite describir cada punto en un espacio de dos dimensiones usando dos coordenadas. Se usan dos ejes de coordenadas que se cruzan en el origen y son perpendiculares entre sí. Generalmente se les llama eje x y eje y. La posición de cualquier punto se da con un par de números reales que indican la distancia de ese punto desde el origen a lo largo de cada eje.
Otro sistema muy usado es el sistema de coordenadas polares. Este sistema describe un punto por su distancia desde el origen y el ángulo que forma con una línea de referencia.
El plano en el espacio tridimensional
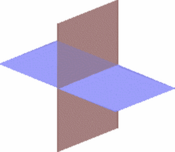
En la geometría euclidiana, un plano es una superficie plana que se extiende infinitamente en dos dimensiones. Los planos a menudo aparecen como partes de un espacio tridimensional. Un buen ejemplo para entenderlo es imaginar una de las paredes de tu habitación, pero pensando que se extiende sin fin y que no tiene grosor.
Formas en el plano
El círculo
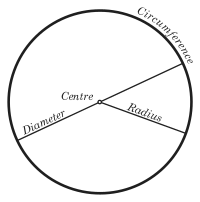
El círculo es una de las formas más conocidas en dos dimensiones. En un plano, un círculo tiene una longitud alrededor de su borde (llamada circunferencia) y un área en su interior. La fórmula para calcular el área de un círculo es:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = \pi r^{2}
donde  es el radio (la distancia desde el centro hasta cualquier punto del borde).
es el radio (la distancia desde el centro hasta cualquier punto del borde).
Otras formas curvas
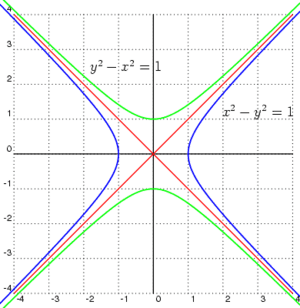
Además del círculo, existen muchas otras formas curvas en dos dimensiones. Algunas de las más importantes son las secciones cónicas: la elipse (como un círculo estirado), la parábola (la forma de un arco o de la trayectoria de un objeto lanzado) y la hipérbola (dos curvas separadas que se abren hacia afuera).
Propiedades del plano en el espacio tridimensional
En un espacio euclidiano tridimensional (como el mundo en el que vivimos), los planos tienen algunas propiedades interesantes:
- Dos planos pueden ser paralelos (nunca se cruzan) o se cruzan en una línea recta.
- Una recta puede ser paralela a un plano, cruzarlo en un solo punto, o estar completamente dentro del plano.
- Si dos rectas son perpendiculares al mismo plano, entonces esas dos rectas son paralelas entre sí.
- Si dos planos son perpendiculares a la misma recta, entonces esos dos planos son paralelos entre sí.
Posición de dos planos
Si tenemos dos planos, pueden estar en diferentes posiciones relativas:
- Planos coincidentes: Son el mismo plano, uno encima del otro.
- Planos paralelos: Nunca se tocan, como el suelo y el techo de una habitación.
- Planos secantes: Se cruzan en una línea recta, como dos paredes que forman una esquina.
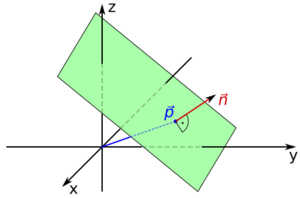
Distancia de un punto a un plano
Podemos calcular la distancia más corta desde un punto hasta un plano. Si el punto está en el plano, la distancia es cero. Si no, la distancia es la longitud de la línea más corta que va desde el punto hasta el plano, formando un ángulo recto con él.
Semiplano
Un semiplano es cada una de las dos partes en que una recta divide a un plano. Imagina una línea dibujada en una hoja de papel infinita; esa línea divide la hoja en dos mitades.
¿Cómo se divide un plano?
Una recta divide un plano en tres partes:
- La propia recta.
- Un semiplano a un lado de la recta.
- El otro semiplano al otro lado de la recta.
Cualquier punto en el plano estará en una de estas tres partes. Si dos puntos están en el mismo semiplano, la línea que los une no cruzará la recta divisoria. Pero si dos puntos están en semiplanos diferentes, la línea que los une sí cruzará la recta.
El plano en la teoría de grafos
En la teoría de grafos, un grafo plano es un tipo de dibujo que se puede hacer en un plano de tal manera que sus líneas (llamadas "aristas") solo se crucen en sus puntos finales (llamados "nodos"). Es como dibujar un mapa sin que los caminos se superpongan, excepto donde se encuentran en una intersección.
Véase también
 En inglés: Euclidean plane Facts for Kids
En inglés: Euclidean plane Facts for Kids
- Geometría plana
- Geometría analítica
- Espacio euclídeo
- Recta
- Punto
- Superficie (matemática)