Geometría euclidiana para niños

La geometría euclidiana es un sistema de matemáticas que lleva el nombre del antiguo matemático griego Euclides. Él la describió en su famoso libro llamado Los Elementos. El método de Euclides se basa en tomar un pequeño grupo de ideas básicas que parecen verdaderas (llamadas axiomas o postulados) y, a partir de ellas, demostrar muchas otras afirmaciones (llamadas teoremas).

Aunque muchas de las ideas de Euclides ya se conocían antes, él fue el primero en organizarlas de forma lógica. Cada resultado se "prueba" usando los axiomas y los teoremas que ya se habían demostrado. Por más de dos mil años, la geometría euclidiana fue la única conocida.

La geometría euclidiana estudia las propiedades de las formas en el espacio euclídeo, como el plano (dos dimensiones) y el espacio tridimensional que conocemos. A veces, los matemáticos usan el término "geometría euclidiana" para hablar de geometrías con propiedades similares en más dimensiones.

Hoy en día, sabemos que existen otras geometrías no euclidianas que también son válidas. Las primeras se descubrieron a principios del siglo XIX. Por ejemplo, la teoría de la relatividad general de Albert Einstein sugiere que el espacio físico no es exactamente euclidiano, aunque la geometría euclidiana es una buena aproximación para distancias cortas.

Detalle de La escuela de Atenas de Rafael que muestra a un matemático griego, quizás representando a Euclides o Arquímedes, usando un compás para dibujar una construcción geométrica.

Los Elementos de Euclides comienza con la geometría plana, que todavía se enseña en las escuelas. También incluye la geometría sólida de tres dimensiones. Gran parte de Los Elementos explica conceptos de álgebra y teoría de números usando un lenguaje geométrico.

La geometría euclidiana es un tipo de geometría sintética. Esto significa que parte de axiomas que describen propiedades básicas de objetos como puntos y líneas, y luego deduce proposiciones sobre ellos. Esto es diferente de la geometría analítica, que fue creada por René Descartes casi 2000 años después y usa coordenadas para describir las formas con fórmulas de álgebra.

Fragmento de Los elementos de Euclides, escrito en papiro, hallado en el yacimiento de Oxirrinco (Egipto).

Geometría del plano: ¿Qué es?

La geometría plana es la parte de la geometría que estudia las figuras y formas que se encuentran en un plano, es decir, en dos dimensiones. Es como dibujar en una hoja de papel. La geometría plana es una parte importante de la geometría euclidiana.

Los Elementos de Euclides: Un libro clave

Los Elementos es una organización de conocimientos de geometría que ya existían. Fue tan bueno que los trabajos anteriores se perdieron. El libro tiene 13 partes, llamadas "libros":

Libros sobre geometría plana

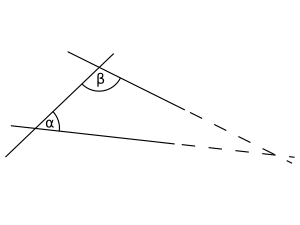
• Libros I–IV y VI: Hablan de la geometría plana. Aquí se demuestran muchas cosas sobre figuras planas, como que "en cualquier triángulo, la suma de dos ángulos cualesquiera es menor que dos ángulos rectos". También se encuentra el famoso teorema de Pitágoras, que dice que "en los triángulos rectángulos, el cuadrado del lado más largo (hipotenusa) es igual a la suma de los cuadrados de los otros dos lados".

Libros sobre números

• Libros V y VII-X: Tratan sobre la teoría de números. Los números se representan con longitudes de líneas o áreas de figuras. Se explican conceptos como los números primos y se demuestra que hay infinitos números primos.

Libros sobre geometría sólida

• Libros XI–XIII: Se refieren a la geometría sólida, que estudia las figuras en tres dimensiones. Un ejemplo es la relación entre el volumen de un cono y un cilindro con la misma altura y base. También se construyen los sólidos platónicos.

Axiomas: Las ideas básicas

Portada de Los elementos de Euclides, publicada en 1570 por Sir Henry Billingsley.

La geometría euclidiana se basa en un sistema de axiomas. Un sistema axiomático es un conjunto de afirmaciones que se aceptan como verdaderas sin necesidad de demostración. A partir de ellas, se deducen lógicamente otras afirmaciones.

Euclides propuso cinco ideas básicas, llamadas "nociones comunes":

1. Si dos cosas son iguales a una tercera, entonces son iguales entre sí.
2. Si a cosas iguales se les añade la misma cantidad, los resultados son iguales.
3. Si a cosas iguales se les quita la misma cantidad, los resultados son iguales.
4. Las cosas que coinciden perfectamente son iguales.
5. El todo es siempre mayor que cualquiera de sus partes.

Los expertos de hoy saben que los axiomas de Euclides no eran completamente suficientes. Euclides usó otras ideas que le parecían obvias, pero que no definió. Por eso, en el siglo XIX, matemáticos como David Hilbert crearon sistemas de axiomas más completos para la geometría.

Postulados: Reglas para construir formas

Los postulados son reglas simples que se aceptan sin demostración y que describen cómo existen ciertos objetos geométricos.

Euclides estableció cinco postulados en su sistema:

1. Dados dos puntos, se puede dibujar una recta que los una.
2. Cualquier segmento de línea puede extenderse indefinidamente en cualquier dirección.
3. Se puede dibujar una circunferencia con cualquier centro y cualquier radio.
4. Todos los ángulos rectos son iguales entre sí.
5. Si una recta corta a otras dos y forma, del mismo lado, dos ángulos internos que suman menos de dos ángulos rectos, entonces esas dos rectas se cortarán en ese lado si se extienden lo suficiente.

El postulado de las paralelas (Postulado 5): Si dos rectas intersecan a una tercera de tal manera que la suma de los ángulos internos de un lado es menor que dos ángulos rectos, entonces las dos rectas inevitablemente deben intersecarse en ese lado si se extienden lo suficiente.

El último postulado, conocido como el postulado de las paralelas, se puede reformular así:

5. Por un punto que está fuera de una recta, se puede trazar una única recta paralela a la recta dada.

Para los matemáticos antiguos, el postulado de las paralelas parecía menos obvio que los demás. Querían demostrarlo a partir de los otros postulados, pero hoy sabemos que eso es imposible. Existen geometrías donde este postulado es verdadero y otras donde es falso. Estas últimas se llaman geometrías no euclidianas.

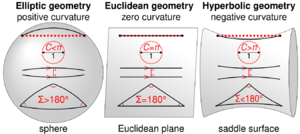
Tipos de geometrías no euclidianas

• Geometría elíptica: En esta geometría, no existe ninguna recta paralela a una dada que pase por un punto exterior.
• Geometría hiperbólica: Aquí, por un punto exterior a una recta, pueden pasar varias rectas paralelas a la recta dada.

Como estas geometrías son válidas, se demuestra que el quinto postulado es una regla independiente que no se puede deducir de las otras cuatro.

Aplicaciones de la geometría euclidiana

La geometría euclidiana es muy importante y se usa en muchos campos.

• 

  Un topógrafo.

• 

  El empaque de esferas se aplica en una pila de naranjas.

• 

  Un espejo parabólico concentra los rayos de luz paralelos en un punto.

• Topografía: Es el estudio de la superficie de la Tierra para hacer mapas. La geometría euclidiana ayuda a medir distancias y ángulos en el terreno.
• Empaquetamiento: Se usa para saber cómo organizar objetos de la manera más eficiente, como las naranjas en una caja.
• Óptica geométrica: Explica cómo la luz se enfoca a través de lentes y espejos.
• Arquitectura: La geometría es fundamental en el diseño de edificios y estructuras.
• Origami: El arte de doblar papel también usa principios geométricos. Algunos problemas que no se pueden resolver con regla y compás, sí se pueden resolver con origami.
• Diseño y fabricación asistidos por computadora (CAD/CAM): Estas herramientas, esenciales para diseñar coches, aviones, barcos y teléfonos, se basan en la geometría euclidiana.

• 

  La geometría se utiliza en el arte y la arquitectura.

• 

  Piezas de motor diseñadas con geometría.

Notación y términos

Cómo nombrar puntos y formas

Para nombrar los puntos, se usan letras mayúsculas del alfabeto (por ejemplo, A, B, C). Las formas, como líneas, triángulos o cuadrados, se nombran usando los puntos que las forman. Por ejemplo, un triángulo tiene tres puntos (A, B y C) que forman sus vértices.

Ángulos complementarios y suplementarios

• Los ángulos complementarios son dos ángulos que, al sumarse, dan como resultado un ángulo recto (90 grados).
• Los ángulos suplementarios son dos ángulos que, al sumarse, dan como resultado un ángulo llano (180 grados).

Nombres modernos de las líneas

Hoy en día, llamamos a las líneas de diferentes maneras:

• Recta: Una línea que se extiende infinitamente en ambas direcciones.
• Semirrecta: Una línea que comienza en un punto y se extiende infinitamente en una dirección.
• Segmento de recta: Una parte de una línea que tiene un principio y un final.

Euclides a veces se refería a las líneas que se extendían "a una longitud suficiente" en lugar de decir "hasta el infinito".

Medidas y cálculos

La geometría euclidiana tiene dos tipos de medidas principales: los ángulos y las distancias. La medida de los ángulos es absoluta, y Euclides usaba el ángulo recto como unidad básica. La medida de las distancias es relativa; se elige una longitud como unidad y las demás se miden en relación con ella.

Un ejemplo de congruencia. Las dos figuras de la izquierda son congruentes, mientras que la tercera es similar a ellas y la cuarta no lo es. Las congruencias cambian algunas propiedades, como la ubicación y la orientación, pero dejan otras sin cambios, como la distancia y los ángulos. Este último tipo de propiedades se denominan invariantes y estudiarlas es la esencia de la geometría.

Las medidas de área y volumen se obtienen a partir de las distancias. Por ejemplo, el área de un rectángulo se calcula multiplicando su ancho por su largo.

Euclides decía que dos figuras eran "iguales" si tenían la misma longitud, área o volumen. El término "congruente" es más fuerte y significa que una figura tiene el mismo tamaño y forma que otra. Es decir, si pudieras mover una figura y colocarla exactamente sobre la otra, serían congruentes. Las figuras que tienen la misma forma pero diferente tamaño se llaman "similares".

Desarrollos posteriores

Matemáticos importantes

• Arquímedes (c. 287-212 a. C.): Fue un gran matemático que calculó volúmenes y áreas de muchas figuras.
• Apolonio de Perge (c. 262-190 a. C.): Conocido por su estudio de las secciones cónicas (como círculos, elipses, parábolas e hipérbolas).

Una esfera tiene 2/3 del volumen y el área superficial del cilindro que la circunscribe. Una esfera y un cilindro fueron colocados sobre la tumba de Arquímedes a petición suya.

El siglo XVII: René Descartes

René Descartes. Retrato según Frans Hals, 1648.

René Descartes (1596-1650) creó la geometría analítica. Este método alternativo usa coordenadas cartesianas (x, y) para representar puntos y ecuaciones para líneas y otras formas. Así, la geometría se puede estudiar usando el álgebra.

En el siglo XVII, Girard Desargues introdujo la geometría proyectiva, que añade puntos, líneas y planos "ideales" en el infinito. Esto ayudó a simplificar algunas demostraciones en la geometría euclidiana.

El siglo XVIII: Límites y construcciones

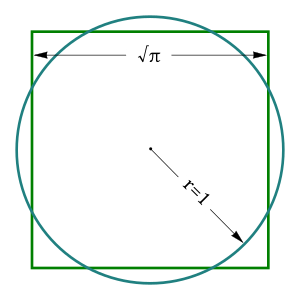
En el siglo XVIII, los matemáticos intentaron demostrar el quinto postulado de Euclides a partir de los otros cuatro, pero no lo lograron. También se preguntaron qué construcciones se podían hacer con solo una regla y un compás. Se descubrió que algunos problemas clásicos, como la trisección de un ángulo (dividirlo en tres partes iguales) o la cuadratura del círculo (construir un cuadrado con la misma área que un círculo dado), son imposibles de resolver solo con estas herramientas.

Cuadratura del círculo: las áreas de este cuadrado y este círculo son iguales. En 1882, se demostró que esta figura no se puede construir en un número finito de pasos con una regla y un compás idealizados.

El siglo XIX: Más dimensiones y nuevas geometrías

A principios del siglo XIX, János Bolyai y Nikolái Lobachevski publicaron trabajos sobre geometría no euclidiana, donde el postulado de las paralelas no es válido. Esto demostró que el postulado de las paralelas no se puede probar a partir de los otros.

También en este siglo, matemáticos como Ludwig Schläfli extendieron la geometría euclidiana a dimensiones superiores, más allá de las tres que conocemos. Él estudió los "politopos", que son como los polígonos (en 2D) y los poliedros (en 3D) pero en más dimensiones.

Comparación de geometrías elíptica, euclidiana e hiperbólica en dos dimensiones

El siglo XX y la relatividad

La teoría de la relatividad especial de Albert Einstein introdujo un espacio-tiempo de cuatro dimensiones que no es euclidiano. Esto mostró que las geometrías no euclidianas, que antes se consideraban solo curiosidades matemáticas, también son útiles para describir el mundo físico.

Una refutación de la geometría euclidiana como descripción del espacio físico. En una prueba de 1919 de la teoría general de la relatividad, las estrellas (marcadas con líneas horizontales cortas) fueron fotografiadas durante un eclipse solar. Los rayos de luz de las estrellas fueron desviados por la gravedad del Sol en su camino hacia la Tierra. Esto se interpreta como evidencia a favor de la predicción de Einstein de que la gravedad provocaría desviaciones de la geometría euclidiana.

En la Teoría de la Relatividad General, la geometría del espacio-tiempo no es euclidiana. Por ejemplo, si se forma un triángulo con tres rayos de luz, sus ángulos interiores no siempre sumarán 180 grados debido a la gravedad. Los campos gravitacionales débiles, como los de la Tierra o el Sol, se describen con una geometría que es casi euclidiana, pero no exactamente. Las predicciones de Einstein sobre estas desviaciones fueron confirmadas por observaciones, como la ligera desviación de la luz de las estrellas por el Sol durante un eclipse solar en 1919.

El infinito en geometría

Objetos infinitos

Euclides a veces hablaba de "líneas finitas" y "líneas infinitas". Aunque sus postulados no mencionan explícitamente líneas infinitas, algunos interpretan que el postulado 3 (la existencia de un círculo con cualquier radio) implica que el espacio es infinito.

Procesos infinitos

Una de las razones por las que el postulado de las paralelas parecía menos seguro es que verificarlo físicamente requeriría inspeccionar dos líneas para asegurarse de que nunca se cruzan, incluso a una distancia muy grande, lo que tomaría un tiempo infinito.

Diferencia entre "euclidiano" y "euclídeo"

Estatua de Euclides hecha por Joseph Durham, en el Museo Natural de Historia de la Universidad de Oxford.

Aunque ambas palabras se refieren a algo relacionado con el matemático griego Euclides, la Real Academia Española solo reconoce "euclidiano" como la forma correcta.

Véase también

En inglés: Euclidean geometry Facts for Kids

• Espacio euclídeo
• Geometría clásica
• Geometría no euclidiana
• Teorema de la mariposa