Fractal para niños

Un fractal es una figura geométrica que tiene una característica muy especial: su forma básica, aunque parezca irregular o rota, se repite una y otra vez en diferentes tamaños. Imagina una rama de árbol; si miras de cerca, verás que las ramitas más pequeñas tienen una forma similar a la rama grande.
La palabra "fractal" la inventó el matemático Benoît Mandelbrot en 1975. Viene del latín fractus, que significa "quebrado" o "fracturado". Aunque el nombre es nuevo, los matemáticos ya conocían estas formas desde hace mucho tiempo.
Contenido
¿Qué son los Fractales?
Los fractales son objetos geométricos que tienen algunas características únicas:
- Son tan irregulares que no se pueden describir con las formas geométricas que conocemos, como círculos o cuadrados.
- Son autosimilares: esto significa que una parte pequeña del fractal se parece mucho a la figura completa, solo que en un tamaño diferente.
Tipos de Autosimilitud en Fractales
La autosimilitud puede presentarse de varias maneras:
- Autosimilitud exacta: El fractal se ve exactamente igual sin importar cuánto lo acerques. Es como si cada parte fuera una copia perfecta del todo.
- Cuasiautosimilitud: El fractal se parece a sí mismo en diferentes escalas, pero con pequeñas variaciones o deformaciones. Es como si las copias no fueran perfectas, pero sí muy parecidas.
- Autosimilitud estadística: En este caso, el fractal no se ve idéntico, pero sus propiedades numéricas o estadísticas (como su "rugosidad") se mantienen al cambiar la escala. Esto es común en fractales que se forman de manera aleatoria.
¿Cómo se definen los fractales?
Los fractales se pueden crear usando un conjunto de reglas sencillas que se repiten una y otra vez. A esto se le llama un algoritmo recursivo. No basta con una sola de estas características para que algo sea un fractal. Por ejemplo, una línea recta es autosimilar (cualquier parte de una línea es una línea), pero no es un fractal porque no es irregular ni tiene una "dimensión fractal" especial.
Fractales en la Naturaleza
Muchos elementos de la naturaleza tienen formas fractales. Las nubes, las montañas, las costas, los copos de nieve, los árboles y hasta nuestro sistema circulatorio son ejemplos de fractales naturales. Estas formas son aproximadas, porque en la naturaleza no hay un detalle infinito como en los fractales matemáticos.
Ejemplos Clásicos de Fractales
Los primeros ejemplos de fractales aparecieron a finales del siglo XIX.
- La curva de Koch (creada por Helge von Koch en 1904) es un buen ejemplo. Se construye empezando con una línea y luego añadiendo pequeños triángulos en el medio de cada segmento, una y otra vez. El resultado es una forma que parece un copo de nieve.
- El triángulo de Sierpinski y la alfombra de Sierpinski (creados por Waclaw Sierpinski en 1915 y 1916) son otros ejemplos famosos. Se construyen quitando partes de una figura inicial de forma repetitiva.
| Construcción de la alfombra de Sierpinski: | |||||
 |
 |
 |
 |
 |
|
| Paso 1 (semilla) | Paso 2 | Paso 3 | Paso 4 | Paso 5 | |
Conjuntos de Julia y Mandelbrot

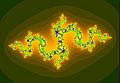
En los años 1920, los matemáticos Pierre Fatou y Gaston Julia estudiaron unos conjuntos que hoy conocemos como conjuntos de Julia. Estos se forman al repetir una y otra vez una operación matemática sencilla. Si el resultado de esta operación no se va al infinito, el punto pertenece al conjunto de Julia.
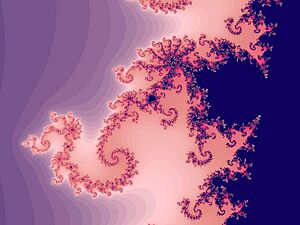
Más tarde, en los años 1980, el conjunto de Mandelbrot se hizo muy popular. Este conjunto es como un "mapa" de los conjuntos de Julia. Cada punto en el conjunto de Mandelbrot nos dice algo sobre el conjunto de Julia que le corresponde.
Ejemplos de conjuntos de Julia para 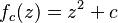
-
En blanco, conjunto de Julia relleno asociado a fc, c=1-φ, donde φ es el número áureo
Aplicaciones de los Fractales
Los fractales no son solo figuras bonitas; tienen usos prácticos en la ciencia y la tecnología.
Compresión de Imágenes
Una de las aplicaciones más interesantes es la compresión de imágenes. Si una imagen tiene formas autosimilares (como el helecho de Barnsley), se puede guardar mucha información de forma muy eficiente. En lugar de guardar cada detalle, se guardan las reglas matemáticas que generan la imagen. Esto permite que la imagen ocupe menos espacio.
Modelado de Formas Naturales
Como ya vimos, la naturaleza está llena de fractales. Los científicos usan la geometría fractal para entender y modelar cómo crecen los árboles, cómo se forman las nubes, cómo se distribuyen los ríos o incluso cómo se pliegan las proteínas. Esto ayuda a comprender mejor el mundo que nos rodea.
Algunos fenómenos naturales que muestran características fractales son:
- Árboles
- Costas
- Montañas
- Nubes
- Copos de nieve
- Ríos
- Relámpagos
- Vasos sanguíneos
- El brócol romanesco
En el Arte y la Música
Los fractales también han inspirado a artistas y músicos.
- En la música, algunos compositores han usado ideas fractales para crear melodías y ritmos que se repiten en diferentes escalas. Se dice que obras de compositores clásicos como Bach o Mozart tienen estructuras fractales.
- En el arte digital, existen programas de computadora como Apophysis o Ultra Fractal que permiten crear imágenes fractales impresionantes y coloridas. El artista neerlandés Maurits Cornelis Escher también exploró estructuras matemáticas complejas en sus famosas litografías.
Galería de imágenes
|
|
|
| Características |
• Dimensiones fractales (Assouad • Recuento de cajas • Correlación • Hausdorff • Empaquetado • Topológicas) • Recursión • Autosimilitud |
|---|---|
| Sistema iterativo de funciones |
• Helecho de Barnsley • Conjunto de Cantor • Copo de nieve de Koch • Esponja de Menger • Alfombra de Sierpinski • Triángulo de Sierpinski • Tamiz de Apolonio • Palabra de Fibonacci • Curva de llenado del espacio • Curva del manjar blanco • Curva de De Rham • Minkowski • Curva del dragón • Curva de Hilbert • Curva de Koch • Curva de Lévy C • Curva de Moore • Curva de Peano • Curva de Sierpinski • T-cuadrada • n-copo • Fractal de Vicsek • Hexacopo • Curva de Gosper • Árbol de Pitágoras |
| Atractor |
• Análisis multifractal |
| Sistema-L |
• Dosel fractal • Curva de llenado del espacio • Árbol H |
| Fractales por tiempo de escape |
• Fractal del barco en llamas • Conjunto de Julia • Fractal de Newton • Conejo de Douady • Fractal de Lyapunov • Conjunto de Mandelbrot • Punto de Misiurewicz • Conjunto multibrot • Fractal de Newton • Tricornio • Mandelcaja • Mandelbulbo |
| Técnicas de renderización |
• Buddhabrot • Trampa orbital • Tallo de Pickover |
| Fractales aleatorios |
• Movimiento browniano • Árbol browniano • Motor browniano • Paisaje fractal • Vuelo de Lévy • Teoría de la percolación • Camino autoevitante |
| Autores destacados |
•Michael Barnsley •Georg Cantor •Bill Gosper •Felix Hausdorff •Desmond Paul Henry •Gaston Julia •Helge von Koch •Paul Lévy •Aleksandr Liapunov •Benoît Mandelbrot •Hamid Naderi Yeganeh •Lewis Fry Richardson •Waclaw Sierpinski |
| Otros |
• "¿Cuánto mide la costa de Gran Bretaña?" • Paradoja de la línea de costa •Anexo:Fractales por dimensión de Hausdorff • La belleza de los fractales (libro de 1986) •Fractalismo • Caos: la creación de una ciencia (libro de 1987) • La geometría fractal de la naturaleza (libro de 1982) • Caleidoscopio • Teoría del caos |
Véase también
 En inglés: Fractal Facts for Kids
En inglés: Fractal Facts for Kids
- Anexo:Fractales por dimensión de Hausdorff
- Desarrollo de fractales mediante el método de Mandelbrot
- Caos y fractales
- ¿Cuánto mide la costa de Gran Bretaña?
- Grafo simétrico
- Dimensión
- Paisaje fractal
- Recursividad
- Sistema de funciones iteradas
- Sistema-L
- Cosmología fractal
- Relatividad de escala
- Teoría del caos