Curva para niños
En matemática, una curva es como una línea continua que cambia de dirección poco a poco. Imagina un camino que no es recto, sino que se dobla suavemente. Las curvas se estudian en la geometría, que es la parte de las matemáticas que se encarga de las formas y los espacios.
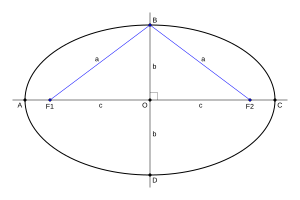
Algunos ejemplos de curvas que se cierran sobre sí mismas son la elipse (como la forma de un balón de rugby), la circunferencia (un círculo perfecto) o el óvalo. Otras curvas son abiertas, lo que significa que no se cierran, como la parábola (la forma que hace una pelota cuando la lanzas al aire) o la hipérbola. Una recta se puede considerar un tipo especial de curva, tan "plana" que su curvatura es cero.
Contenido
¿Qué es una curva?
Una curva es una línea que se extiende en una sola dirección y que cambia su rumbo de forma gradual. Piensa en el camino que sigue un coche al girar o en el dibujo que haces con un lápiz sin levantarlo del papel.
¿Cómo se define una curva?
En matemáticas, una curva se puede definir como el camino que sigue un punto que se mueve. Este camino se puede describir con ecuaciones. Por ejemplo, si sabes dónde está el punto en cada momento, puedes dibujar la curva.
Historia de las curvas
Las curvas han sido importantes para los matemáticos desde hace mucho tiempo. Aquí te mostramos algunos momentos clave:
| Año | Acontecimiento |
|---|---|
| 300 a. C. | Euclides estudió las formas que se obtienen al cortar un cono, como círculos y elipses. |
| 250 a. C. | Arquímedes investigó las curvas con forma de espiral. |
| 225 a. C. | Apolonio de Perge escribió un libro muy importante sobre las curvas cónicas. |
| 1704 | Isaac Newton clasificó diferentes tipos de curvas. |
| 1890 | Giuseppe Peano demostró que incluso un cuadrado se puede "dibujar" con una sola curva. |
| Década de 1920 | Pável Urysón y Karl Menger ayudaron a definir las curvas usando ideas de la topología, que estudia las propiedades de las formas que no cambian cuando se estiran o doblan. |
¿Cómo se expresan las curvas?
Las curvas se pueden describir de varias maneras usando ecuaciones:
- Forma implícita: Es una ecuación donde las variables x e y están mezcladas, como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x^2 + y^2 - 25 = 0 (que es un círculo).
- Forma explícita: Aquí, una variable (normalmente y) se expresa en función de la otra (x), como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = 2x + 1 (que es una línea recta).
- Forma paramétrica: Se usan ecuaciones separadas para x e y, que dependen de una tercera variable llamada "parámetro" (por ejemplo, t). Esto es útil para describir el movimiento de un punto.
Tipos de curvas
Curva plana
Una curva plana es una curva que se puede dibujar completamente en una superficie plana, como una hoja de papel. Puede ser abierta o cerrada. Por ejemplo, el dibujo de una función matemática en una gráfica es una curva plana.
Curva cerrada
Una curva es cerrada si su punto de inicio y su punto final son el mismo. Imagina dibujar un círculo o un corazón sin levantar el lápiz y terminando donde empezaste. Si además la curva no se cruza a sí misma, se llama curva cerrada simple. Un ejemplo es una elipse.
Curva suave
Una curva suave es una curva que no tiene "picos" o "esquinas" afiladas. Es decir, no cambia de dirección de forma brusca. Piensa en un círculo o una parábola; son suaves. Una curva que no es suave podría ser una cicloide, que tiene puntos donde la dirección cambia de golpe.
Si una curva es suave en todas sus partes, se dice que es suave por partes.
Curvas en el espacio
Las curvas no solo existen en un plano. También pueden existir en el espacio tridimensional, como el camino que sigue un avión en el aire. Para estudiar estas curvas, los matemáticos usan herramientas especiales.
Vectores de una curva
Para entender cómo se mueve una curva en el espacio, se usan tres vectores (flechas que indican dirección y magnitud) que son perpendiculares entre sí:
- Vector tangente: Indica la dirección en la que se mueve la curva en un punto específico. Es como la dirección de la velocidad de un objeto que se mueve por esa curva.
- Vector normal: Indica hacia dónde se "dobla" la curva.
- Vector binormal: Es perpendicular a los otros dos y completa un sistema de referencia para entender la curva.
Estos tres vectores forman un "marco móvil" que ayuda a describir la forma y el movimiento de la curva en cada punto.
Curvas especiales
Algunas curvas son tan complejas que no se pueden describir con las herramientas normales. Por ejemplo, la curva de Koch es una curva que es tan "rugosa" que tiene una longitud infinita, ¡aunque ocupa un espacio finito! Estas curvas son parte de un campo llamado geometría fractal.
|
Véase también
 En inglés: Curve Facts for Kids
En inglés: Curve Facts for Kids