Geometría esférica para niños

La geometría esférica es el estudio de las formas y figuras que se dibujan sobre la superficie de una esfera, como si fuera un balón gigante. Es un tipo especial de geometría que no sigue todas las reglas de la geometría plana que aprendemos en la escuela, la que se usa para dibujar en una hoja de papel.

En la geometría plana, los elementos básicos son los puntos y las líneas rectas. En una esfera, los puntos son los mismos. Sin embargo, lo que llamamos "líneas" en la esfera son diferentes. No son rectas como las que dibujamos con una regla. En su lugar, usamos las "trayectorias más cortas" entre dos puntos, que se llaman geodésicas. En una esfera, estas geodésicas son los grandes círculos. Un gran círculo es como el Ecuador en la Tierra: un círculo que divide la esfera en dos mitades iguales.

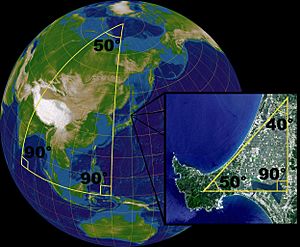
Así, en la geometría esférica, los ángulos se forman entre estos grandes círculos. Por eso, la trigonometría esférica (que estudia los triángulos en la esfera) es diferente de la trigonometría plana. Por ejemplo, si dibujas un triángulo en la superficie de una esfera, la suma de sus tres ángulos siempre será mayor de 180 grados.

En una esfera, la suma de los ángulos de un triángulo no es igual a 180°. Una esfera no es un espacio euclidiano, pero localmente las leyes de la geometría euclidiana son buenas aproximaciones. En un pequeño triángulo en la cara de la Tierra, la suma de los ángulos es muy cercana a 180°. Una esfera puede ser representada por una colección de mapas de dos dimensiones, por lo tanto una esfera es una variedad, en el triángulo curvo convexo la suma de los ángulos puede ser superior a 180°.

¿Por qué la geometría esférica es diferente?

La geometría esférica es un ejemplo de geometría no euclídea. Esto significa que no sigue el quinto postulado de Euclides, que dice que por un punto exterior a una línea solo se puede trazar una línea paralela a la primera. En la geometría esférica, no existen líneas paralelas. Si dibujas dos grandes círculos en una esfera, siempre se cruzarán en dos puntos opuestos.

Aplicaciones de la geometría esférica

La geometría esférica es muy útil en la vida real. Tiene aplicaciones importantes en:

• Navegación: Los barcos y aviones usan la geometría esférica para encontrar las rutas más cortas entre dos lugares en la Tierra, ya que nuestro planeta es una esfera (o casi).
• Astronomía: Para entender el movimiento de los planetas y las estrellas en el cielo, los científicos usan la geometría esférica.

Geometría relacionada: El plano proyectivo real

Existe otra geometría interesante relacionada con la esférica, llamada plano proyectivo real. Se obtiene si consideramos que los puntos opuestos en una esfera (como el Polo Norte y el Polo Sur) son el mismo punto. Aunque localmente se parece mucho a la geometría esférica, globalmente tiene propiedades diferentes.

Véase también

En inglés: Spherical geometry Facts for Kids

• Trigonometría esférica
• Distancia de gran círculo
• Poliedro esférico
• Geometría hiperbólica
• Geometría no euclídea
• Geometría riemanniana
• Geodésica
• Topología