Botella de Klein para niños
La botella de Klein es un objeto matemático muy interesante que pertenece a una rama de las matemáticas llamada topología. Imagina una superficie que no tiene un "adentro" ni un "afuera" definidos, ¡es como si todo fuera una sola cara! A diferencia de una pelota, que tiene un interior y un exterior claros, la botella de Klein es una superficie "no orientable". Esto significa que si un pequeño insecto caminara sobre ella, podría ir de un lado al otro sin cruzar ningún borde.
Otros objetos similares que también son no orientables incluyen la banda de Möbius. La diferencia principal es que una banda de Möbius tiene un solo borde, mientras que la botella de Klein no tiene ningún borde, ¡es una superficie cerrada! Una esfera tampoco tiene borde, pero la esfera sí es orientable (tiene un interior y un exterior).
La botella de Klein fue descrita por primera vez en 1882 por un matemático alemán llamado Felix Klein. Curiosamente, su nombre original en alemán era "Superficie de Klein" (Kleinsche Fläche). Pero cuando se tradujo por primera vez al inglés, el traductor confundió la palabra "Fläche" (superficie) con "Flasche" (botella). Como la forma que vemos de la botella de Klein se parece mucho a una botella, el error se mantuvo y así la conocemos hoy.
Contenido
¿Cómo se construye una botella de Klein?
Para entender cómo se forma una botella de Klein, podemos imaginar un proceso de "pegado" de un cuadrado.
Pasos para crear una botella de Klein
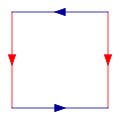
Imagina que tienes un cuadrado. Para construir una botella de Klein, debes pegar sus bordes de una manera especial:
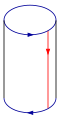
- Primero, pegas los lados opuestos del cuadrado (por ejemplo, el lado izquierdo con el derecho) para formar un cilindro.
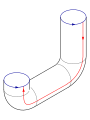
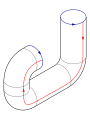
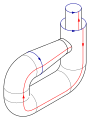
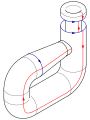
- Luego, tomas los dos extremos circulares de ese cilindro y los pegas entre sí. Pero aquí viene lo complicado: para que las flechas de los bordes coincidan, uno de los extremos debe pasar a través del lado del cilindro antes de unirse al otro extremo.
Visualizando la autointersección
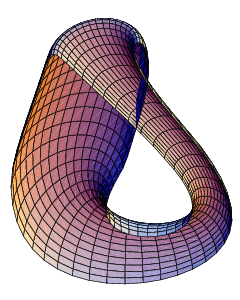
Cuando intentamos hacer esto en nuestro espacio tridimensional (el mundo en el que vivimos), la botella de Klein parece cruzarse a sí misma. Esta "autointersección" es solo una forma de visualizarla en 3D. La verdadera botella de Klein, en un espacio con más dimensiones, no se cruza a sí misma.
La botella de Klein en cuatro dimensiones
Piensa en una línea que se cruza a sí misma en un dibujo en papel (que es un espacio bidimensional). Puedes "deshacer" esa intersección levantando una parte de la línea fuera del papel. De manera similar, si tuviéramos una cuarta dimensión, la botella de Klein podría pasar a través de sí misma sin crear un agujero o una intersección real. Simplemente "empujaríamos" suavemente una parte de la botella fuera de nuestro espacio tridimensional.
Esta forma de verla nos ayuda a entender sus propiedades. Por ejemplo, no tiene bordes y es una superficie de una sola cara.
-
Paso 1: Un cuadrado con bordes marcados.
-
Paso 2: Se pegan dos lados opuestos para formar un cilindro.
-
Paso 3: Se doblan los extremos del cilindro.
-
Paso 4: Un extremo se pasa a través del cilindro.
-
Paso 5: Los extremos se unen.
-
Paso 6: La botella de Klein terminada (con autointersección en 3D).
¿Qué pasa si cortamos una botella de Klein?
Si cortamos una botella de Klein por la mitad a lo largo de su línea de simetría, ¡obtenemos dos bandas de Möbius! Cada una de estas bandas es como un reflejo de la otra. También es posible cortar una botella de Klein de otra manera y obtener una única banda de Möbius.
Otro concepto con un nombre similar
En otra área de las matemáticas, la geometría algebraica, existe algo llamado "superficie de Klein". Aunque suena parecido, es diferente de la botella de Klein. Una superficie de Klein es similar a una superficie de Riemann y tiene propiedades matemáticas más avanzadas relacionadas con funciones complejas.
Véase también
En inglés: Klein bottle Facts for Kids
