Teoría de grupos para niños
En el álgebra abstracta, la teoría de grupos es una rama de las matemáticas que estudia una estructura muy importante llamada grupo. Un grupo es un conjunto de elementos que tienen una sola operación, como la suma o la multiplicación, que sigue ciertas reglas.
Esta teoría se encarga de clasificar los grupos, entender sus propiedades y ver cómo se usan dentro y fuera de las matemáticas. Por ejemplo, algunos sistemas físicos, como los cristales y los átomos de hidrógeno, pueden explicarse usando grupos de simetría. También es útil para entender tres de las cuatro fuerzas fundamentales del universo. Por eso, la teoría de grupos es muy importante en física, química y en la ciencia de los materiales. También es clave para la criptografía de clave pública, que se usa para proteger información.
La historia de la teoría de grupos comenzó en el siglo XIX. Uno de los logros más grandes de las matemáticas en el siglo XX fue la clasificación de grupos simples finitos. Fue un trabajo enorme en el que participaron más de 100 matemáticos.
Contenido
Historia de los grupos matemáticos
Las ideas de la teoría de grupos vienen de la teoría de ecuaciones algebraicas, la teoría de números y la geometría. Matemáticos como Euler, Gauss, Lagrange, Abel y Galois fueron los primeros en sentar las bases de esta área.
Pioneros y sus contribuciones
Galois es reconocido por ser el primero en conectar esta teoría con la teoría de cuerpos, creando la teoría de Galois. Él también usó el nombre "grupo". Otros matemáticos importantes que contribuyeron fueron Cayley, Emil Artin, Emmy Noether y Ludwig Sylow.
En 1882, Walter Dick dio la definición moderna de grupo. A finales del siglo XIX, Frobenius definió el concepto de grupo abstracto usando un conjunto de reglas básicas.
Orígenes en la resolución de ecuaciones
Los primeros estudios sobre grupos de permutaciones (formas de ordenar elementos) fueron hechos por Lagrange, Ruffini y Abel. Ellos buscaban cómo resolver ecuaciones polinómicas complejas. Évariste Galois inventó el término "grupo" y conectó esta nueva teoría con la teoría de campos, lo que hoy conocemos como teoría de Galois.
La importancia de los grupos en la geometría
En la geometría, los grupos se volvieron importantes en la geometría proyectiva y la geometría no euclidiana. Felix Klein propuso que la teoría de grupos fuera un principio fundamental para organizar la geometría.
Galois, en la década de 1830, fue el primero en usar grupos para saber si las ecuaciones polinómicas podían resolverse. Arthur Cayley y Augustin Louis Cauchy continuaron estas investigaciones, creando la teoría de los grupos de permutaciones.
Otra fuente histórica de los grupos viene de situaciones geométricas. Para entender diferentes geometrías (como la euclidiana, la hiperbólica o la geometría proyectiva) usando la teoría de grupos, Felix Klein inició el programa de Erlangen.
La teoría de grupos se unificó alrededor de 1880. Desde entonces, su impacto ha crecido mucho, dando origen a otras áreas como el álgebra abstracta y la teoría de la representación.
¿Qué es un grupo?
Un grupo es un conjunto de elementos, por ejemplo, números o formas, junto con una operación (como sumar o multiplicar) que cumple tres reglas importantes:
- Asociatividad: Si tienes tres elementos a, b y c, no importa cómo los agrupes al operarlos. Por ejemplo, (a + b) + c es lo mismo que a + (b + c).
- Elemento neutro: Hay un elemento especial en el conjunto que, al operarlo con cualquier otro elemento, no lo cambia. Por ejemplo, en la suma, el 0 es el elemento neutro (5 + 0 = 5).
- Elemento simétrico (o inverso): Para cada elemento en el conjunto, existe otro elemento que, al operarlos juntos, dan como resultado el elemento neutro. Por ejemplo, en la suma, el simétrico de 5 es -5 (5 + (-5) = 0).
Si un grupo también cumple la propiedad conmutativa (el orden de los elementos no cambia el resultado, como a + b = b + a), se le llama grupo abeliano o conmutativo.
Cómo se escriben los grupos
Se usa la notación aditiva cuando la operación se escribe como "+" y el elemento neutro es "0". La notación multiplicativa usa "·" o simplemente "ab" para la operación, y el elemento neutro es "1" o "e".
Ejemplos de grupos
- El conjunto de los números enteros (
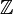) con la suma (+) es un grupo abeliano. El 0 es el elemento neutro y el simétrico de un número x es -x. - El conjunto de los números reales (
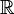) con la suma (+) también es un grupo abeliano. - El conjunto de los números enteros sin el 0, con la multiplicación (·), NO es un grupo. Esto es porque el simétrico de un número x sería 1/x, y 1/x no siempre es un número entero (por ejemplo, 1/2 no es entero).
- El conjunto de todas las formas de reordenar los elementos de un conjunto X (llamadas biyecciones), junto con la composición de funciones, forma un grupo. Si X tiene más de dos elementos, este grupo no es abeliano. Se llama grupo simétrico.
Conexiones entre grupos
Entre dos grupos, puede haber funciones especiales llamadas homomorfismos. Una función es un homomorfismo si es compatible con las operaciones de ambos grupos. Esto significa que si operas dos elementos en el primer grupo y luego aplicas la función, obtienes el mismo resultado que si aplicas la función a cada elemento por separado y luego los operas en el segundo grupo.
Si un homomorfismo es también una biyección (es decir, cada elemento del primer grupo se conecta con un único elemento del segundo grupo, y viceversa), se le llama isomorfismo. Cuando dos grupos son isomorfos, significa que tienen la misma estructura, aunque sus elementos y operaciones se llamen de forma diferente.
Clases principales de grupos
Los grupos se pueden clasificar por su orden, que es la cantidad de elementos que tienen. Pueden ser finitos (si tienen un número limitado de elementos) o infinitos.
Grupos de permutación
Los primeros grupos que se estudiaron a fondo fueron los grupos de permutaciones. Una permutación es una forma de reordenar los elementos de un conjunto. Si tienes un conjunto X y una colección de reordenamientos que puedes combinar y deshacer, esa colección forma un grupo. Por ejemplo, si X tiene n elementos y consideras todas las posibles permutaciones, formas el grupo simétrico Sn.
Grupos de matrices
Otra clase importante son los grupos de matrices. Aquí, los elementos del grupo son matrices que se pueden invertir (tienen un determinante diferente de cero). Estas matrices se pueden multiplicar entre sí y sus inversas también están en el grupo. Estos grupos son muy útiles para entender las transformaciones lineales en el espacio.
Grupos abstractos
Al principio, los grupos se veían como colecciones concretas de números, permutaciones o matrices. Pero a finales del siglo XIX, surgió la idea de un grupo abstracto. Esto significa que la naturaleza de los elementos no importa; lo que importa son las reglas que cumplen. Dos grupos que tienen la misma estructura (son isomorfos) se consideran el mismo grupo abstracto.
Grupos con estructura adicional
A veces, un grupo tiene una estructura extra, como si fuera un espacio topológico o una múltiple diferenciable. Si las operaciones del grupo (multiplicación e inversión) son compatibles con esta estructura adicional, entonces el grupo se convierte en un grupo topológico, un grupo de Lie o un grupo algebraico.
Teoría geométrica de los grupos
Las investigaciones más recientes en la teoría de grupos usan técnicas de la topología, que es el estudio de las propiedades de los espacios que se conservan bajo deformaciones continuas. Una forma de crear nuevos grupos a partir de otros conocidos es mediante los productos libres y las extensiones HNN.
Se pueden aplicar muchas técnicas topológicas porque se sabe que siempre es posible construir un espacio topológico (como un CW-complejo de dos dimensiones) cuyo grupo fundamental sea el grupo que se está estudiando.
Véase también
En inglés: Group theory Facts for Kids
- Grupo
- Representación de grupo
- Subgrupo
- Álgebra abstracta
- Teoría geométrica de grupos
Galería de imágenes
-
Un dibujo especial llamado grafo de Cayley, que ayuda a entender un tipo de grupo matemático.
