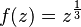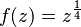Superficie de Riemann para niños
Una superficie de Riemann es un tipo especial de superficie matemática que se usa para estudiar funciones que trabajan con números complejos. Imagina que es como una versión "estirada" o "doblada" del plano donde dibujamos los números complejos.
Estas superficies fueron estudiadas por primera vez por el matemático Bernhard Riemann, de quien toman su nombre. Aunque localmente, es decir, si miras una parte muy pequeña de ellas, parecen un trozo plano, globalmente pueden tener formas muy diferentes, como una esfera, una rosquilla (un toro) o varias láminas unidas.
Lo más interesante de las superficies de Riemann es que son el lugar perfecto para entender cómo se comportan ciertas funciones especiales, llamadas funciones holomorfas. Estas funciones son muy "suaves" y predecibles. Son especialmente útiles para estudiar funciones que pueden tener varios resultados para un mismo número, como la raíz cuadrada o el logaritmo natural.
Toda superficie de Riemann es una superficie real de dos dimensiones, pero tiene una característica extra, llamada "estructura compleja", que es necesaria para definir bien las funciones holomorfas. Una superficie real de dos dimensiones puede convertirse en una superficie de Riemann si se puede "orientar" (es decir, tiene dos lados, como una hoja de papel, no como una banda de Möbius) y se pueden medir distancias en ella. Por ejemplo, una esfera o una rosquilla pueden ser superficies de Riemann, pero una banda de Möbius o una botella de Klein no.
Contenido
- Historia de las superficies de Riemann
- ¿Qué es una superficie de Riemann?
- ¿Cómo se definen las superficies de Riemann?
- Propiedades de las superficies de Riemann
- Relación entre lo analítico y lo algebraico
- Ejemplos de superficies de Riemann
- Clasificación de superficies de Riemann
- Clasificación según las funciones
- Véase también
Historia de las superficies de Riemann
El concepto de superficie de Riemann empezó a desarrollarse a mediados del siglo XIX. El matemático Bernhard Riemann buscaba una forma de extender el área donde ciertas funciones matemáticas, llamadas funciones analíticas, podían trabajar. Se dio cuenta de que la mejor manera de hacerlo no era sobre el plano complejo normal, sino sobre copias de partes de este plano que se superponían, formando lo que hoy conocemos como una superficie de Riemann.
¿Qué es una superficie de Riemann?
Una superficie de Riemann es una superficie de dos dimensiones que se puede "orientar", lo que significa que tiene un "lado" y otro, como una hoja de papel. Gracias a esta propiedad, se le puede añadir una "estructura compleja" que permite trabajar con números complejos de una manera especial.
Por ejemplo, una esfera o una rosquilla (toro) pueden tener esta estructura compleja. Sin embargo, objetos como la banda de Möbius o la botella de Klein no pueden, porque no son orientables de la misma manera.
Se sabe que una esfera solo tiene una forma de ser una superficie de Riemann, pero otras superficies, como las que parecen rosquillas con más agujeros, pueden tener infinitas formas de serlo.
Las superficies de Riemann son el lugar ideal para estudiar cómo se comportan muchas funciones matemáticas de forma global. Por ejemplo, funciones como:
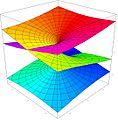
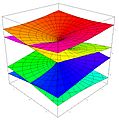
- La raíz cuadrada de un número complejo:
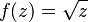
- El logaritmo de un número complejo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(z)=\log(z)
¿Cómo se definen las superficies de Riemann?
Hay varias maneras de definir una superficie de Riemann, pero todas son equivalentes:
Definición basada en el espacio complejo
Una superficie de Riemann X es un espacio conectado y "ordenado" (llamado espacio de Hausdorff) que tiene una dimensión compleja de uno. Esto significa que:
- Para cada punto de la superficie, hay una pequeña área a su alrededor que se parece mucho a un círculo plano en el plano complejo.
- Tenemos un conjunto de "mapas" (llamados cartas) que nos permiten pasar de la superficie a este círculo plano.
- Cuando dos de estos "mapas" se superponen, la forma en que se conectan entre sí (las "transiciones") debe ser "holomorfa", es decir, muy suave y bien definida para los números complejos.
Definición basada en la estructura conforme
Una superficie de Riemann es una superficie real de dos dimensiones que se puede orientar, y que además tiene una "estructura conforme". Esto significa que:
- La superficie tiene una forma de medir los ángulos en cualquier punto.
- Esta forma de medir ángulos se mantiene incluso si la superficie se estira o se encoge, siempre que no se rompa.
Una estructura compleja (la de la primera definición) siempre nos da una estructura conforme. Demostrar lo contrario, que una estructura conforme nos da una estructura compleja, es más complicado.
Propiedades de las superficies de Riemann
Orientabilidad
Toda superficie de Riemann es "orientable" como una superficie real. Esto significa que siempre podemos distinguir un "lado" del otro, como el anverso y el reverso de una hoja de papel. Esto es importante porque asegura que las funciones se comporten de manera consistente en toda la superficie.
Funciones en superficies de Riemann
En una superficie de Riemann que no es "compacta" (es decir, que se extiende infinitamente, como un plano), siempre existen funciones holomorfas que no son constantes. Esto significa que estas funciones pueden cambiar de valor.
Sin embargo, en una superficie de Riemann "compacta" (que no se extiende infinitamente, como una esfera o una rosquilla), cualquier función holomorfa que dé como resultado un número complejo debe ser constante. Esto se debe a un principio llamado "principio del máximo". Pero en estas superficies compactas, siempre existen funciones "meromorfas" que no son constantes. Las funciones meromorfas son como las holomorfas, pero pueden tener algunos "agujeros" o puntos donde su valor es infinito.
Relación entre lo analítico y lo algebraico
El hecho de que existan funciones meromorfas no constantes en superficies de Riemann compactas es muy importante. Permite demostrar que cualquier superficie de Riemann compacta puede ser descrita mediante ecuaciones polinómicas, como las que se usan en geometría algebraica. De hecho, se puede demostrar que toda superficie de Riemann compacta puede "encajarse" en un espacio complejo de tres dimensiones.
Esto es sorprendente: las superficies de Riemann se definen localmente (por "parches"), pero si son compactas, ¡resulta que también son "algebraicas"! Esto permite estudiarlas usando herramientas tanto del análisis matemático como de la geometría algebraica.
Un ejemplo es el toro (la forma de una rosquilla). Las funciones especiales que se definen en él, llamadas funciones elípticas de Weierstrass, pueden relacionarse con ecuaciones polinómicas, mostrando la conexión entre estas dos ramas de las matemáticas.
Ejemplos de superficies de Riemann
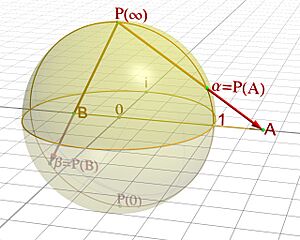
- La esfera de Riemann: Imagina una esfera. Podemos definirla como una superficie de Riemann. Si tomamos el plano complejo y le añadimos un punto extra que representa el "infinito", obtenemos la esfera de Riemann. Es una superficie de Riemann compacta muy importante.
- Espacios cocientes: Si tenemos una superficie de Riemann y un grupo de transformaciones que la mueven sin dejar puntos fijos, el resultado de "pegar" los puntos que se corresponden por estas transformaciones es otra superficie de Riemann.
* Por ejemplo, si tomamos el plano complejo y lo "doblamos" pegando los puntos que están a una distancia fija (como si enrolláramos una hoja de papel para hacer un cilindro, y luego pegáramos los extremos del cilindro), podemos obtener un toro. La forma del toro no cambia, pero la "estructura compleja" sí puede variar.
- Extensiones analíticas: Muchas superficies de Riemann no compactas se obtienen extendiendo el dominio de funciones analíticas.
Clasificación de superficies de Riemann
Las superficies de Riemann se pueden clasificar en tres tipos principales: hiperbólicas, parabólicas y elípticas. Esta clasificación se basa en un teorema muy importante llamado "teorema de uniformización". Este teorema dice que cualquier superficie de Riemann que sea "simplemente conexa" (es decir, que no tenga agujeros, como una esfera o un plano) es equivalente a una de estas tres:
- El plano complejo (todos los números complejos).
- La esfera de Riemann (el plano complejo más el punto del infinito).
- El disco abierto (todos los números complejos dentro de un círculo).
Si una superficie de Riemann no es simplemente conexa (es decir, tiene agujeros, como un toro), entonces su "recubridor universal" (una superficie más grande y sin agujeros que la "cubre") será equivalente a uno de los tres modelos anteriores. La superficie original se obtiene "doblando" este recubridor universal de una manera especial.
- Superficies elípticas: Son las que se parecen a la esfera. Las transformaciones que las mantienen iguales siempre dejan un punto fijo, por lo que no podemos obtener otras superficies "doblando" la esfera.
- Superficies parabólicas: Son las que se parecen al plano. Se obtienen "doblando" el plano con traslaciones (movimientos sin rotación). Los resultados son superficies que parecen coronas circulares o toros.
- Superficies hiperbólicas: Son las que se parecen al disco. Se obtienen "doblando" el disco con un tipo especial de transformaciones llamadas "grupos Fuchsianos". Estas superficies tienen una geometría diferente, llamada geometría hiperbólica.
Clasificación según las funciones
Además de la clasificación geométrica, existe otra clasificación de las superficies de Riemann que usan los analistas (matemáticos que estudian funciones). En esta clasificación, una superficie de Riemann se llama "parabólica" si no tiene ciertas funciones especiales que no sean constantes, y "hiperbólica" en caso contrario.
Esta clasificación se basa en cómo se comportan las funciones en la superficie. Por ejemplo, una superficie de Riemann que consiste en "todos los números complejos excepto el 0 y el 1" es parabólica según esta clasificación, pero hiperbólica según la clasificación geométrica. Es importante no confundir ambas clasificaciones.
Véase también
 En inglés: Riemann surface Facts for Kids
En inglés: Riemann surface Facts for Kids