Ecuación algebraica para niños

Enciclopedia para niños

Una ecuación algebraica es como un rompecabezas matemático. Imagina que tienes una expresión con números y letras, como por ejemplo, x elevado a alguna potencia, y todo eso está igualado a cero. Tu misión es encontrar el valor o los valores de la letra x que hacen que esa igualdad sea cierta.

En matemáticas, especialmente en el Álgebra, una ecuación algebraica es una expresión de la forma P(x) = 0. Aquí, P(x) es lo que llamamos un Polinomio, que es una suma de términos donde la letra x está elevada a diferentes potencias (como x², x³, etc.), y cada término tiene un número que lo acompaña (llamado coeficiente). El "grado" de la ecuación es el número más alto al que está elevada la x. Por ejemplo, si la x más alta es x³, la ecuación es de tercer grado.

Cualquier número que, al reemplazarlo en la x, hace que la ecuación sea verdadera (es decir, que el resultado sea cero), se llama una raíz o solución de la ecuación. Resolver una ecuación significa encontrar todas sus raíces.

Por ejemplo, si tenemos la ecuación:

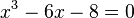
$x^3 - 6x - 8 = 0$

Aquí, el grado es 3 porque x³ es la potencia más alta. Encontrar las raíces de esta ecuación significa hallar los valores de x que hacen que la expresión sea igual a cero.

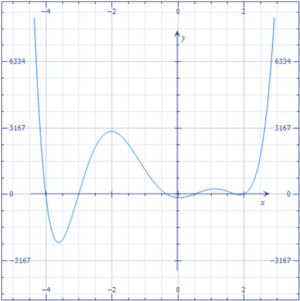
Desde el punto de vista gráfico, si dibujamos la función polinómica 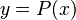$y = P(x)$ en un plano, las raíces reales de la ecuación son los puntos donde la curva toca o cruza el eje horizontal (el eje de las x).

Historia de las Ecuaciones Algebraicas

Las ecuaciones algebraicas de grados más altos tienen una historia muy antigua. Ya en la Mesopotamia (hace miles de años), se encontraron tablillas de arcilla con problemas prácticos que necesitaban resolver este tipo de ecuaciones. De hecho, los mesopotámicos ya sabían cómo encontrar las soluciones generales para ecuaciones de segundo grado.

En la matemática china también se conocían desde hace mucho tiempo las formas de resolver estas ecuaciones. Matemáticos chinos y árabes estudiaron problemas específicos que incluían ecuaciones de tercer grado y de grados aún mayores. Por ejemplo, el matemático chino Li Chih (que vivió entre 1192 y 1279) trabajó con problemas que involucraban ecuaciones de sexto grado.

Sin embargo, las primeras soluciones generales y organizadas para las ecuaciones de tercer y cuarto grado fueron descubiertas por matemáticos italianos en el siglo XVI. Ellos encontraron maneras de resolver estas ecuaciones usando lo que se conoce como "radicales" (que son como las raíces cuadradas, cúbicas, etc.). Al intentar resolver estas ecuaciones, estos matemáticos incluso empezaron a usar por primera vez los números complejos, que son números que incluyen una parte "imaginaria" (como la raíz cuadrada de -1).

Las ecuaciones de quinto grado (y las de grados superiores a 5) resultaron ser mucho más difíciles. No se podían resolver con las mismas fórmulas generales usando radicales. Fue hasta el siglo XIX cuando matemáticos europeos, como Évariste Galois, demostraron por qué esto era así y desarrollaron nuevas formas de entender sus soluciones.

Ecuaciones con una sola incógnita

Cuando hablamos de ecuaciones con una sola incógnita, nos referimos a aquellas donde solo hay una letra desconocida, generalmente x.

Ejemplos de Ecuaciones Algebraicas

Ecuación cúbica: 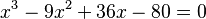$x^3-9x^2+36x-80=0$ . Esta ecuación tiene una solución real y dos soluciones complejas.
Ecuación de quinto grado: 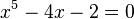$x^5-4x-2=0$ . Esta tiene cinco soluciones: tres reales y dos complejas. Algunas de estas no se pueden encontrar con fórmulas simples de radicales.
Ecuación de séptimo grado: 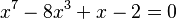$x^7-8x^3 +x -2=0$ . Tiene tres soluciones reales.
Ecuación de sexto grado: 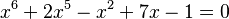$x^6 +2x^5-x^2 +7x-1 =0$ . Tiene una solución positiva y otra negativa.

¿Qué NO es una Ecuación Algebraica?

Algunas ecuaciones no se consideran algebraicas en el sentido estricto, por ejemplo:

Ecuaciones donde los números que acompañan a las x (los coeficientes) no son números enteros o racionales, como $x^2 - \sqrt{3}x -5\sqrt[3]{7} =0$ . Aunque se pueden resolver, no cumplen con la definición más básica de una ecuación algebraica con coeficientes enteros.
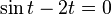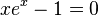Ecuaciones que incluyen funciones que no son polinomios, como las funciones trigonométricas (seno, coseno) o exponenciales. Por ejemplo, $\sin t -2t = 0$ o $xe^x -1 = 0$ no son ecuaciones algebraicas, sino "ecuaciones trascendentes".

Tipos de Ecuaciones según su Grado

Las ecuaciones algebraicas se clasifican según su grado:

Grado 1: 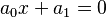$a_0x+a_1=0$ (Ecuación lineal)
Grado 2: 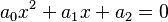$a_0x^2+a_1x+a_2=0$ (Ecuación cuadrática)
Grado 3: 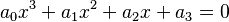$a_0x^3+a_1x^2+a_2x+a_3=0$ (Ecuación cúbica)
Grado 4: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_0x^4+a_1x^3+a_2x^2+a_3x+a_4=0 (Ecuación cuártica)

Resolver ecuaciones de grado 1 y 2 es relativamente sencillo, ya que existen fórmulas directas para encontrar sus soluciones.

Factorización de Polinomios

Un concepto importante es la factorización. Si encuentras una raíz k de una ecuación P(x)=0, significa que puedes dividir el polinomio P(x) entre (x-k) sin que quede residuo. Esto te ayuda a simplificar la ecuación y encontrar las demás raíces. Por ejemplo, si 2 es una raíz de 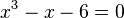$x^3-x-6=0$ , entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (x-2) es un factor del polinomio.

Ecuaciones de Segundo Grado

Las soluciones de una ecuación algebraica de una variable corresponden a los puntos de una curva, que «tocan o cortan» al eje horizontal.

Una Ecuación de segundo grado tiene la forma:

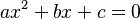
$ax^2+bx+c=0$

Para resolverla, se usa una fórmula muy conocida:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}

Esta fórmula te da hasta dos soluciones. A veces, estas soluciones pueden ser números complejos.

Ecuaciones de Mayor Grado

Ecuación de tercer grado
Ecuación de cuarto grado
Ecuación de quinto grado

Como mencionamos, las ecuaciones de tercer y cuarto grado también tienen fórmulas para sus soluciones, aunque son más complicadas. Matemáticos como Gerolamo Cardano y Lodovico Ferrari las descubrieron en el siglo XVI. Sin embargo, para ecuaciones de quinto grado o mayores, no siempre es posible encontrar las soluciones usando solo radicales, como demostró Évariste Galois a principios del siglo XIX.

Transformación de Coeficientes

Una ecuación algebraica que tiene coeficientes (los números que acompañan a las x) que son fracciones, siempre se puede convertir en una ecuación con coeficientes enteros. Por ejemplo, si tienes:

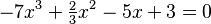
$-7x^3 + \begin{matrix}\frac{2}{3}\end{matrix} x^2 - 5x + 3=0$

Puedes multiplicar toda la ecuación por 3 para eliminar la fracción:

$-21x^3 + 2x^2 - 15x + 9 = 0. \,\!$

Ambas ecuaciones tienen las mismas soluciones.

Ecuaciones Binomias

Las ecuaciones binomias son un tipo especial de ecuaciones algebraicas. Tienen solo dos términos. Por ejemplo:

La ecuación 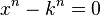$x^n - k^n = 0$ tiene una solución igual a k.
La ecuación 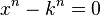$x^n - k^n = 0$ también tiene una solución igual a -k si n es un número par.
La ecuación 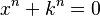$x^n + k^n = 0$ tiene una solución igual a -k si n es un número impar.

Ecuaciones Relacionadas

Ecuaciones Consecuencia: Si todas las soluciones de una ecuación F=0 también son soluciones de otra ecuación G=0, decimos que G=0 es una "consecuencia" de F=0.
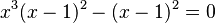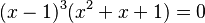Ecuaciones Equivalentes: Si dos ecuaciones tienen exactamente las mismas soluciones, se dice que son "equivalentes". Por ejemplo, $x^3(x-1)^2 -(x-1)^2=0$ y $(x-1)^3(x^2+x+1)=0$ son equivalentes.

Algunas reglas sobre ecuaciones equivalentes y consecuencias:

La ecuación F+G=G es equivalente a F=0.
F/G = 0 es equivalente a F=0 (siempre que G no sea cero).
FG = 0 es equivalente a tener F=0 o G=0.
La ecuación Fⁿ = 0 es una consecuencia de F=0 (si n es un número entero positivo mayor que 2).
La ecuación Fⁿ = Gⁿ es equivalente a F=G si n es impar. Si n es par, es equivalente a F=G y también a F=-G.

Propiedades Importantes

Según el Teorema fundamental del álgebra, toda ecuación algebraica de grado n tiene exactamente n soluciones en el conjunto de los números complejos (contando las soluciones repetidas).
Esto significa que cualquier polinomio de grado n se puede escribir como la multiplicación de n factores simples, como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (x-\alpha_1)(x-\alpha_2)...(x-\alpha_n) , donde cada Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \alpha_i es una solución.
Si una ecuación con coeficientes reales tiene una solución compleja (como $a+bi$ ), entonces su "conjugado" (que es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a-bi ) también será una solución. Las soluciones complejas siempre aparecen en parejas.
Si una ecuación con coeficientes racionales tiene una solución real que incluye una raíz cuadrada (como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p+\sqrt{q} ), entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p-\sqrt{q} también será una solución.

Otros Datos Interesantes

Si una ecuación algebraica con coeficientes reales tiene un grado impar (como 3, 5, 7, etc.), siempre tendrá al menos una solución real. Esto es porque las soluciones complejas siempre vienen en parejas, así que si el número total de soluciones es impar, al menos una debe ser real.
Si una ecuación polinomial con coeficientes enteros tiene una solución entera k, entonces el último número de la ecuación (el término independiente) debe ser divisible por k. Por ejemplo, en 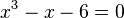$x^3-x-6=0$ , si hay una solución entera, debe ser un divisor de 6 (como ±1, ±2, ±3, ±6). En este caso, 2 es una solución.

Ver también

Galería de imágenes

Las soluciones de una ecuación algebraica de una variable corresponden a los puntos de una curva, que «tocan o cortan» al eje horizontal.

Véase también

En inglés: Algebraic equation Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Ecuación_algebraica&oldid=4948104»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Ecuación algebraica para Niños. Enciclopedia Kiddle.