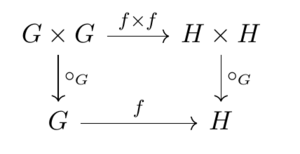Homomorfismo para niños
En matemáticas, un homomorfismo es como un "traductor" especial entre dos conjuntos de cosas que tienen una misma forma de organizarse o de hacer operaciones. Imagina que tienes dos grupos de objetos, y en cada grupo puedes hacer lo mismo con ellos (por ejemplo, sumarlos o multiplicarlos). Un homomorfismo es una función que toma un objeto de un grupo y lo convierte en un objeto del otro grupo, pero de una manera que respeta las operaciones. Es decir, si haces una operación en el primer grupo y luego "traduces" el resultado, es lo mismo que si primero "traduces" los objetos y luego haces la operación en el segundo grupo.
Contenido
¿Qué es un Homomorfismo?
Un homomorfismo es una función que conecta dos estructuras matemáticas similares. Piensa en estas estructuras como conjuntos de elementos que tienen reglas o "operaciones" definidas para combinarlos. Por ejemplo, la suma o la multiplicación son operaciones.
La Idea Principal
La idea clave de un homomorfismo es que "preserva las operaciones". Esto significa que si tomas dos elementos de la primera estructura, los combinas con su operación y luego aplicas la función, el resultado es el mismo que si primero aplicas la función a cada elemento por separado y luego los combinas con la operación de la segunda estructura.
¿Cómo Funciona la Preservación de Operaciones?
Imagina que tienes dos conjuntos, A y B. En el conjunto A, puedes hacer una operación (como sumar). En el conjunto B, también puedes hacer una operación (quizás también sumar, o algo similar). Una función que es un homomorfismo, digamos `f`, hace lo siguiente:
- Si tomas dos números `a` y `b` del conjunto A, y los sumas (`a + b`).
- Luego, aplicas la función `f` al resultado: `f(a + b)`.
- Esto debe ser igual a si primero aplicas la función `f` a `a` y a `b` por separado (`f(a)` y `f(b)`), y luego sumas esos resultados en el conjunto B: `f(a) + f(b)`.
En resumen, `f(a + b) = f(a) + f(b)`. Esto es un ejemplo sencillo de cómo se "preserva" la operación de suma.
Ejemplos Sencillos de Homomorfismos
Aunque los ejemplos avanzados usan conceptos complejos, podemos entender la idea con algo más simple.
Homomorfismos en la Aritmética
Un ejemplo muy básico de una función que "preserva" una operación es la multiplicación por un número.
- Considera la función `f(x) = 2x`.
- Si sumamos dos números `a` y `b`: `f(a + b) = 2 * (a + b) = 2a + 2b`.
- Si aplicamos la función a cada número y luego sumamos: `f(a) + f(b) = 2a + 2b`.
- Como puedes ver, `f(a + b) = f(a) + f(b)`. Esta función preserva la operación de suma.
Esto es una forma muy simplificada de entender cómo una función puede mantener la estructura de las operaciones entre dos conjuntos.
Tipos Especiales de Homomorfismos
Los homomorfismos tienen nombres especiales dependiendo de cómo se comportan:
- Epimorfismo: Es un homomorfismo que "cubre" todo el segundo conjunto. Esto significa que cada elemento del segundo conjunto es el resultado de aplicar la función a al menos un elemento del primer conjunto.
- Monomorfismo: Es un homomorfismo que es "uno a uno". Esto significa que cada elemento diferente en el primer conjunto se mapea a un elemento diferente en el segundo conjunto. No hay dos elementos distintos del primer conjunto que vayan al mismo elemento del segundo.
- Isomorfismo: Es un homomorfismo que es tanto un epimorfismo como un monomorfismo. Es como una "copia perfecta" de una estructura a otra. Si dos estructuras son isomorfas, se consideran matemáticamente idénticas en cuanto a su forma y operaciones.
- Endomorfismo: Es un homomorfismo que va de una estructura a sí misma. Es decir, la función toma elementos de un conjunto y los mapea de vuelta al mismo conjunto, preservando las operaciones.
- Automorfismo: Es un endomorfismo que también es un isomorfismo. Es una "transformación perfecta" de una estructura en sí misma.
Galería de imágenes
Véase también
 En inglés: Homomorphism Facts for Kids
En inglés: Homomorphism Facts for Kids