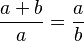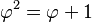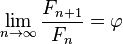Número áureo para niños
El número áureo, también conocido como número de oro, razón dorada o proporción áurea, es un número irracional. Se representa con la letra griega φ (phi) (en minúscula) o Φ (Phi) (en mayúscula), en honor al escultor griego Fidias.
Su valor numérico es aproximadamente 1,618033988749894... Como es un número irracional, no se puede escribir como una fracción exacta ni tiene un número finito de decimales. Sus decimales continúan infinitamente sin repetirse en un patrón.
A veces también se representa con la letra griega tau (Τ τ), que viene de la palabra griega tomé, que significa 'corte' o 'sección'.
Este número tiene muchas propiedades interesantes y fue descubierto en la Antigüedad. No se encontró como un cálculo, sino como una relación o proporción entre dos partes de una línea, es decir, una construcción geométrica. Esta proporción se encuentra en algunas figuras geométricas y también en la naturaleza. Por ejemplo, en las nervaduras de las hojas de algunos árboles, en el grosor de las ramas, en el caparazón de un caracol o en los patrones de los girasoles. Una de sus propiedades más curiosas es que su valor (aproximadamente 1,618...) y su inverso (1/Φ ≈ 0,618...) tienen las mismas cifras decimales después del punto.
Algunas personas creen que los objetos que tienen esta proporción son más bonitos. A lo largo de la historia, se ha dicho que el número áureo se usó en el diseño de obras de arquitectura y otras artes, aunque algunos expertos lo han puesto en duda.
Contenido
¿Qué es el número áureo?
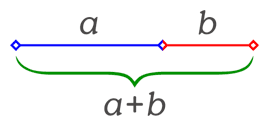
El número áureo es el valor que se obtiene de una proporción especial entre dos segmentos de una línea, llamados a y b. El segmento a es más largo que el b. La relación es la siguiente:
- La longitud total de los dos segmentos (a + b) es al segmento más largo (a), lo mismo que el segmento más largo (a) es al segmento más corto (b). Esto se puede escribir como una ecuación algebraica:
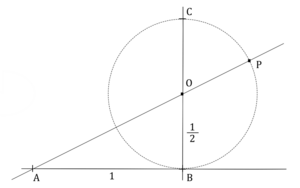
El valor del número áureo (φ) es el resultado de dividir a entre b (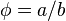
). Se descubre al intentar dividir una línea en dos partes de tal manera que, al dividir la longitud total por la parte más grande, se obtenga el mismo resultado que al dividir la parte más grande por la parte más pequeña.
¿Cómo se calcula el valor del número áureo?
Para calcular el valor del número áureo, partimos de la relación que acabamos de ver:
| 1 | 2 | |
|---|---|---|
| Ecuaciones |  |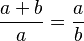
 |
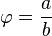| Simplificando |  |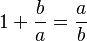
|
| Sustituyendo |  |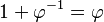
|
Multiplicando  |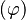
 |
|
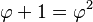| Despejando |  |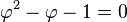
|
| Solución positiva |  |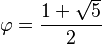
|
Así, el valor del número áureo es:
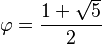- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \approx 1,61803398874989484820 Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 45868343656381177203\ldots
Historia del número áureo
Algunos historiadores creen que el número áureo pudo haber aparecido en estelas antiguas de Babilonia y Asiria hace unos 4000 años. Sin embargo, no hay pruebas claras de que los artistas de esa época lo usaran a propósito. Es fácil encontrar proporciones curiosas al medir objetos complejos, pero para que el número áureo esté realmente presente, las medidas deben ser muy específicas. Por eso, muchos expertos dudan que los babilonios lo conocieran.
El número áureo en la Antigüedad
El primer matemático que estudió formalmente el número áureo fue Euclides (alrededor del 300 al 265 a. C.). Él lo definió así en su libro Los Elementos:
Se dice que una recta ha sido cortada en extrema y media razón cuando la recta entera es al segmento mayor como el segmento mayor es al segmento menor.Euclides Los Elementos Definición 3 del Libro Sexto.
Euclides también demostró que este número no se puede escribir como una fracción de dos números enteros, lo que significa que es un número irracional.
Se cree que Platón (alrededor del 428 al 347 a. C.) pudo haber estudiado el número áureo. El historiador griego Proclo mencionó que Eudoxo "multiplicó el número de teoremas relativos a la sección a los que Platón dio origen". La palabra "sección" (tomé) a menudo se interpretó como la sección áurea. Sin embargo, desde el siglo XIX, esta interpretación ha sido muy debatida, y muchos investigadores creen que no se refería al número áureo. A pesar de esto, Platón consideraba que los números irracionales, descubiertos por los pitagóricos, eran muy importantes para entender el universo.
El número áureo en la Edad Moderna
En 1509, el matemático y teólogo italiano Luca Pacioli publicó un libro llamado De Divina Proportione (La Divina Proporción). En él, Pacioli dio cinco razones por las que consideraba que el número áureo era "divino":
- Su valor es único, como la unicidad de Dios.
- Está definido por tres segmentos de línea, lo que Pacioli asociaba con la Trinidad.
- Es un número irracional (no se puede medir exactamente), lo que Pacioli comparaba con la naturaleza incomprensible de Dios.
- Tiene una propiedad de autosimilitud (partes que se parecen al todo), que Pacioli relacionaba con la presencia constante de Dios.
- Pacioli creía que, así como Dios dio forma al Universo a través de la "quinta esencia" (representada por el dodecaedro), el número áureo dio forma al dodecaedro.
En 1525, Alberto Durero publicó un libro donde explicaba cómo dibujar la espiral áurea usando una regla y un compás. Esta espiral se conoce como "espiral de Durero".
El astrónomo Johannes Kepler (1571-1630) usó el número áureo en su modelo del sistema solar. Él lo describió con gran admiración:
La geometría tiene dos grandes tesoros: uno es el teorema de Pitágoras; el otro, la división de una línea entre el extremo y su proporcional. El primero lo podemos comparar a una medida de plata; el segundo lo debemos denominar una joya preciosa.Johannes Kepler en Mysterium Cosmographicum (El misterio cósmico).
El primer uso conocido de la palabra "áureo" o "dorado" para referirse a este número fue en 1835, por el matemático alemán Martin Ohm. Aunque él sugirió que el término ya era común, es probable que se hiciera popular alrededor de 1830.
Originalmente, el símbolo para el número áureo era τ (tau), de la palabra griega tomé ('corte'). Sin embargo, en 1900, el matemático Mark Barr propuso usar Φ o φ en honor a Fidias. Se le dio este honor a Fidias porque sus esculturas eran consideradas muy bellas, una cualidad que también se atribuía al número áureo.
El número áureo en las matemáticas
Propiedades y representaciones
El número áureo tiene muchas propiedades matemáticas interesantes.
Propiedades aritméticas
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \textstyle \varphi = 1,618033988749894848204586834365638117720309... es el único número real positivo que cumple:
- De esta propiedad se derivan otras:
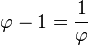
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \varphi^3 = \frac {\varphi + 1} {{\varphi - 1}} \ </A> :<math>\varphi^2 - \frac {1} {\varphi} = 2 \ </A> * Las potencias del número áureo se pueden expresar como una suma de potencias de grados menores del mismo número. Por ejemplo: :<math>\varphi^n = \varphi^{n-1}+\varphi^{n-2}\, (para cualquier número entero n).
Representación mediante fracciones continuas
El número áureo se puede escribir de una forma muy especial usando fracciones continuas:
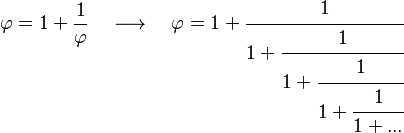
Esta es la fracción continua más simple de todas. Debido a esto, el número áureo es el número más difícil de aproximar con fracciones, lo que lo convierte en el "más irracional".
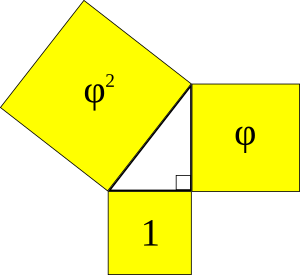
Relación con la sucesión de Fibonacci
La sucesión de Fibonacci es una serie de números donde cada número es la suma de los dos anteriores (0, 1, 1, 2, 3, 5, 8, 13, 21, ...). Si dividimos un número de Fibonacci por el anterior, el resultado se acerca cada vez más al número áureo a medida que avanzamos en la sucesión.
Esta relación fue descubierta por el astrónomo alemán Johannes Kepler. Más de cien años después, el matemático escocés Robert Simson la demostró.
A mediados del siglo XIX, el matemático francés Jacques Philippe Marie Binet redescubrió una fórmula que permite encontrar cualquier número de Fibonacci sin tener que calcular todos los anteriores. Esta fórmula depende directamente del número áureo:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): F_n = \frac{1}{\sqrt{5}} \left [ \left (\frac{1 +\sqrt{5}}{2} \right )^n - \left (\frac{1 - \sqrt{5}}{2}\right )^n \right ] Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): =\frac{\varphi^n - (1-\varphi )^{n} }{\sqrt{5}}
- para n >0 y n es un número entero positivo.
El número áureo en la geometría
El número áureo y la sección áurea aparecen en muchas figuras geométricas regulares que tienen simetría de cinco lados (pentagonal), o donde aparece la raíz cuadrada de cinco.
- Se encuentra en las relaciones entre las partes de un pentágono regular.
- También en las relaciones de un pentagrama (estrella de cinco puntas).
- En las relaciones de un decágono (figura de diez lados).
- Y en las relaciones de los dodecaedros (figura de doce caras) y los icosaedros (figura de veinte caras).
El rectángulo áureo de Euclides
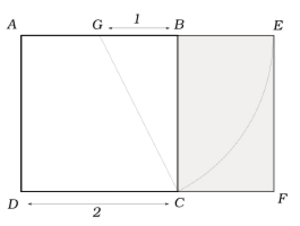
Un rectángulo es "áureo" si la proporción entre su lado más largo y su lado más corto es el número áureo. Euclides explicó cómo construirlo en su libro Los elementos.
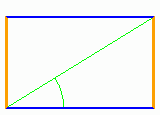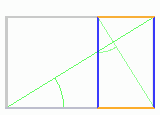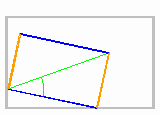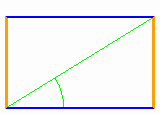
Si un rectángulo es áureo, y le quitamos un cuadrado formado por su lado más corto, el rectángulo que queda también es áureo. Este proceso se puede repetir infinitamente.
En el pentagrama
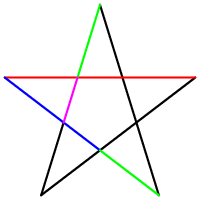
El número áureo es muy importante en los pentágonos regulares y en los pentagramas. Cada vez que dos segmentos se cruzan en un pentagrama, se dividen entre sí en la proporción áurea.
El pentagrama contiene diez triángulos isósceles: cinco con ángulos agudos y cinco con ángulos obtusos. En todos ellos, la relación entre el lado más largo y el más corto es φ. Estos se llaman "triángulos áureos".
Debido a la gran simetría de este símbolo, se puede dibujar una nueva estrella dentro del pentágono central, y este proceso puede repetirse hasta el infinito. De la misma manera, se puede dibujar un pentágono por fuera, que sería el pentágono interior de una estrella más grande. Esto significa que el número áureo aparece infinitas veces en el pentagrama.
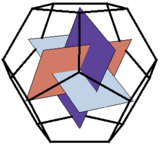
Relación con los sólidos platónicos
El número áureo está relacionado con los sólidos platónicos, especialmente con el icosaedro y el dodecaedro. Las medidas de estos sólidos se pueden expresar usando el número áureo.
Por ejemplo, si tres rectángulos áureos se superponen en sus centros de forma paralela, los 12 puntos de las esquinas de estos rectángulos coinciden exactamente con los puntos de un icosaedro y con los centros de las caras de un dodecaedro.
El número áureo en la naturaleza
En la naturaleza, hay muchos ejemplos donde se observa la sección áurea o los números de Fibonacci:
- Leonardo de Pisa (Fibonacci) usó la sucesión que lleva su nombre para resolver un problema matemático sobre la reproducción de conejos. La división de dos números consecutivos de la sucesión de Fibonacci se acerca al número áureo.
- La forma en que se organizan los pétalos de las flores.
- La distribución de las hojas en un tallo.
- La relación entre las nervaduras de las hojas de los árboles.
- La relación entre el grosor de las ramas principales y el tronco de un árbol.
- La cantidad de espirales en una piña (ocho y trece espirales), o en los patrones de los girasoles. Estos números son parte de la sucesión de Fibonacci.
- La relación entre la distancia del ombligo a los pies de una persona y su altura total.
- La cantidad de pétalos en algunas flores (3, 5, 8, 13, 21, 34, 55, 89 y 144).
- La forma espiralada de las conchas de caracoles o de cefalópodos como el nautilus. Estas espirales suelen seguir una espiral logarítmica que se relaciona con el número áureo.
- Para que las hojas de una planta reciban la mayor cantidad de luz solar con la menor interferencia, crecen en forma de hélice ascendente con un ángulo constante de aproximadamente 137,5 grados. Este ángulo se relaciona con el número áureo.
El número áureo en el arte
- Se ha sugerido que las proporciones de la Gran Pirámide de Guiza podrían estar relacionadas con el número áureo. Algunos matemáticos han defendido esta idea basándose en escritos antiguos, pero las mediciones reales de la pirámide son difíciles de interpretar debido a su tamaño y al desgaste del tiempo.
- Las relaciones entre las partes, el techo y las columnas del Partenón, en Atenas (s. V a. C.), también han sido estudiadas en relación con el número áureo. Se ha descubierto que los constructores griegos usaron correcciones ópticas para que el templo se viera perfecto a la vista, inclinando o curvando ligeramente sus elementos.
- Algunos estudios, como los del Dr. Fechner, sugieren que la percepción de la belleza está relacionada con la proporción áurea. Se cree que las obras de arte, la arquitectura y hasta las personas que se acercan a esta proporción se perciben como más bellas.
- En el cuadro Leda atómica, de Salvador Dalí, se usó el número áureo.
- En las películas "El acorazado Potemkin" e "Iván el Terrible" de Serguéi Eisenstein, se usaron estructuras y tiempos basados en el número áureo.
- En los violines, la ubicación de los orificios en la tapa (las "efes" o "eses") se relaciona con el número áureo.
- Se dice que el número áureo aparece en las proporciones de los objetos y personas en las obras de Miguel Ángel, Durero y Leonardo Da Vinci. Sin embargo, es importante aclarar que en el famoso dibujo del hombre de Vitruvio de Leonardo da Vinci, él siguió las proporciones fraccionarias del cuerpo humano descritas por Vitruvio en su libro.
- En algunas obras musicales de Wolfgang Amadeus Mozart, la Quinta Sinfonía de Ludwig van Beethoven, y obras de Franz Schubert y Claude Debussy, se han encontrado relaciones con el número áureo. Es probable que los compositores las crearan de forma intuitiva, buscando un equilibrio en el sonido.
- En la novela El código Da Vinci de Dan Brown, se mencionan los números de Fibonacci y el número áureo como una pista importante. Se explica cómo el número áureo aparece en la naturaleza y en el cuerpo humano.
- En el episodio “Sabotaje” de la serie de televisión NUMB3RS, el personaje Charlie Eppes menciona que el número áureo se encuentra en los cristales, las galaxias y la concha del Nautilus.
- En el episodio "Obra maestra" de la serie Mentes Criminales, los crímenes siguen la sucesión de Fibonacci, y las ubicaciones se disponen según una espiral áurea.
- En la película Pi, fe en el caos, el personaje principal, un matemático, explica la relación entre los números de Fibonacci y la sección áurea.
- En el manga JoJo's Bizarre Adventure (parte 7, Steel Ball Run), la espiral dorada es un elemento clave de la trama.
- El número phi aparece en la película de Disney Donald en el país de las matemáticas.
Véase también
En inglés: Golden ratio Facts for Kids
- Triángulo de Kepler
- Número π
- Número e
- Búsqueda de la sección dorada
- Espiral logarítmica
- Sucesión de Fibonacci
- Composición áurea
- Pitágoras
- Luca Pacioli
- Matila Ghyka
- Roger Penrose
- Decágono regular
- Rectángulo cordobés
- Número metálico
