Espiral logarítmica para niños
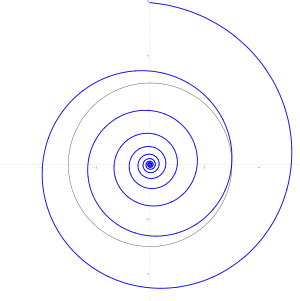
Una espiral logarítmica, también conocida como espiral equiangular o espiral de crecimiento, es un tipo especial de curva en forma de espiral que se encuentra muy a menudo en la naturaleza. Su nombre "logarítmica" viene de una de las formas en que se puede describir con una ecuación matemática.
Contenido
Historia de la Espiral Logarítmica
La espiral logarítmica ha fascinado a muchos pensadores a lo largo de la historia. El nombre "espiral logarítmica" fue propuesto por Pierre Varignon.
¿Quiénes Estudiaron la Espiral Logarítmica?
Grandes matemáticos como René Descartes y Evangelista Torricelli estudiaron esta curva. Sin embargo, fue Jakob Bernoulli, un famoso matemático suizo, quien le dedicó un estudio profundo. Él la llamó Spira mirabilis, que significa "la espiral maravillosa".
Bernoulli estaba tan impresionado con esta espiral que quiso que se grabara en su tumba. Eligió la frase en latín Eadem mutata resurgo, que significa "Mutante y permanente, vuelvo a resurgir siendo el mismo". Esto simbolizaba cómo la espiral logarítmica crece y cambia, pero siempre mantiene su forma. Curiosamente, los artesanos que hicieron su tumba grabaron por error una espiral de Arquímedes en lugar de una logarítmica.
Diferencia entre Espirales
La diferencia principal entre una espiral logarítmica y una espiral de Arquímedes es cómo crecen sus brazos. En una espiral logarítmica, la distancia entre sus vueltas aumenta de forma multiplicativa (como en una progresión geométrica). En cambio, en una espiral de Arquímedes, la distancia entre las vueltas es siempre la misma.
¿Cómo se Describe una Espiral Logarítmica?
Las espirales logarítmicas se pueden describir con ecuaciones matemáticas.
Ecuaciones Básicas
En un sistema de coordenadas polares (que usa una distancia r desde el centro y un ángulo θ), la fórmula de la curva puede escribirse como:
- `r = a b^θ`
Aquí, 'a' y 'b' son números.
- `a` es un factor que cambia el tamaño de la espiral.
- `b` controla qué tan rápido se enrolla la espiral y en qué dirección. Si `b` es mayor que 1, la espiral se expande a medida que el ángulo θ aumenta. Si `b` es menor que 1, la espiral se contrae.
Ángulo Constante
Una característica muy especial de la espiral logarítmica es que si dibujas una línea desde el centro hasta cualquier punto de la espiral, el ángulo entre esa línea y la curva de la espiral siempre será el mismo. Por eso también se le llama "espiral equiangular" (equiangular significa "ángulos iguales").
Características Interesantes
La espiral logarítmica tiene propiedades matemáticas muy curiosas.
El Grado de la Espiral
El "grado" de una espiral logarítmica es el ángulo constante que forma con los círculos que tienen su centro en el origen. Este ángulo nos dice qué tan "apretada" o "abierta" es la espiral. Por ejemplo, una espiral logarítmica de grado 0 es un círculo perfecto.
Distancia Finita al Origen
Aunque una espiral logarítmica se enrolla infinitas veces hacia su centro, la distancia total que recorrerías si siguieras la espiral desde un punto hasta el centro es finita. Esto fue descubierto por Torricelli antes de que se desarrollara el cálculo moderno.
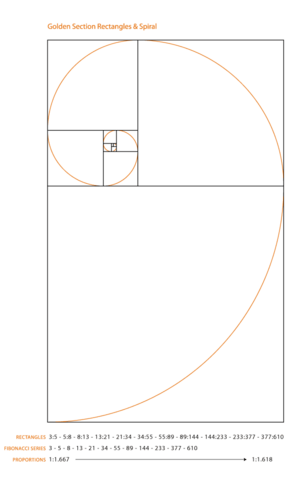
Conexión con la Proporción Áurea
Las espirales logarítmicas están relacionadas con la proporción áurea y la sucesión de Fibonacci. Se pueden construir espirales que se parecen mucho a la logarítmica usando rectángulos basados en la proporción áurea.
Espirales Logarítmicas en la Naturaleza
La espiral logarítmica es una forma muy común en la naturaleza, lo que demuestra la belleza de las matemáticas en el mundo real.
En el Espacio
- Las galaxias espirales, como nuestra propia Vía Láctea, tienen brazos que se parecen mucho a espirales logarítmicas.
- Los ciclones tropicales (como los huracanes) también forman espirales logarítmicas en sus nubes.
En la Biología
- Las conchas de muchos moluscos, como el nautilus, crecen siguiendo una espiral logarítmica. Esto ocurre porque el animal va añadiendo nuevas cámaras a su concha, cada una un poco más grande que la anterior, manteniendo siempre la misma forma general.
- Las telas de araña a menudo tienen una estructura que se aproxima a una espiral logarítmica.
- Los girasoles tienen patrones de semillas que forman espirales logarítmicas.
- Los halcones se acercan a sus presas volando en una trayectoria que es una espiral logarítmica. Esto les permite mantener a su presa en el mejor ángulo de visión mientras se acercan.
- Los insectos a veces vuelan en espirales logarítmicas alrededor de luces artificiales. Esto sucede porque están acostumbrados a volar manteniendo un ángulo constante con fuentes de luz lejanas como el Sol o la Luna. Cuando la luz está cerca, como una bombilla, este comportamiento los hace volar en círculos cada vez más cerrados.
En la Tierra
- En la geotecnia (el estudio del suelo y las rocas), las superficies de falla (donde el suelo se rompe bajo presión) a menudo tienen la forma de una espiral logarítmica.
Galería de imágenes
-
Una parte de un fractal de Mandelbrot, que puede mostrar espirales logarítmicas.
-
La Galaxia de Bode (M81), donde se observa polvo interestelar siguiendo una espiral logarítmica.
-
Una borrasca sobre Islandia, cuyo patrón se aproxima a una espiral logarítmica.
-
El símbolo de Debian se parece a una espiral logarítmica.
Véase también
En inglés: Logarithmic spiral Facts for Kids
