Autosimilitud para niños
En Matemática, la autosimilitud es una propiedad fascinante donde un objeto se parece a sí mismo en diferentes escalas. Imagina que tomas una pequeña parte de algo y, al hacerla más grande, ¡se ve exactamente igual que el objeto completo! Esto es lo que significa la autosimilitud.
Muchos objetos en la naturaleza, como las costas marítimas, muestran esta característica de forma estadística. Esto quiere decir que, aunque no sean copias perfectas, sus partes tienen propiedades similares a las del todo. La autosimilitud es una característica clave de los fractales, que son formas geométricas con patrones que se repiten infinitamente.
Contenido
Autosimilitud: ¿Qué es y por qué es fascinante?
La autosimilitud es la cualidad de un objeto de ser similar a una o varias de sus partes. Es como si pudieras hacer zoom en una imagen y encontrar el mismo patrón una y otra vez, sin importar cuánto te acerques. Esta idea nos ayuda a entender cómo se forman muchas cosas en la naturaleza y en las matemáticas.
Tipos de autosimilitud: ¿Cómo se presenta?
Aunque la idea principal es la misma, la autosimilitud puede presentarse de diferentes maneras. Aquí te explicamos los tipos más comunes:
Autosimilitud exacta: ¡Igualito!
Cuando hablamos de autosimilitud exacta, significa que una parte de un objeto es una copia idéntica del objeto completo. Si amplías esa parte, verás que es exactamente igual al original.
Un ejemplo famoso es el copo de nieve de Koch. Si tomas un pequeño segmento de su borde y lo amplías, verás que tiene la misma forma compleja que todo el borde. Otro ejemplo es el Triángulo de Sierpinski, donde cada triángulo más pequeño es una réplica perfecta del triángulo grande.
Autosimilitud aproximada: Casi igual
La autosimilitud aproximada es muy común en la naturaleza. Aquí, las partes se parecen al todo, pero no son copias perfectas. Hay pequeñas diferencias.
Piensa en un brócoli romanesco: cada florete pequeño tiene una forma similar a la del brócoli completo, pero no es una réplica exacta. Esta pequeña variación hace que se vea natural y orgánico.
Autosimilitud estadística: Parecido en promedio
Este tipo de autosimilitud es el menos estricto. Significa que, aunque los detalles exactos no se repitan, ciertas propiedades estadísticas (como la rugosidad o la forma general) se mantienen similares a diferentes escalas.
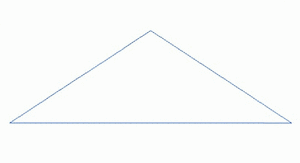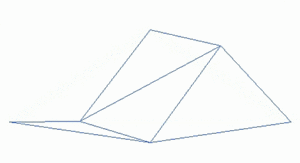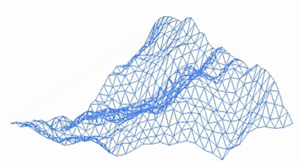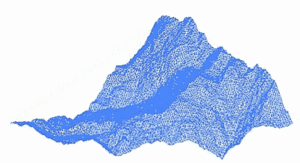
Las montañas son un buen ejemplo. Si miras una cadena montañosa desde lejos, y luego te acercas a una sola montaña, y luego a una roca en esa montaña, verás que la forma general y la textura rocosa se mantienen, aunque los detalles específicos sean diferentes. Lo mismo ocurre con los cráteres de la Luna.
Ejemplos de autosimilitud en el mundo real
La autosimilitud no es solo un concepto matemático; la encontramos en muchos lugares inesperados.
El Conjunto de Mandelbrot: Un patrón infinito
El conjunto de Mandelbrot es uno de los fractales más famosos. Si haces zoom en sus bordes, descubrirás que aparecen copias más pequeñas y distorsionadas del conjunto original. Es un ejemplo impresionante de autosimilitud exacta que parece no tener fin.
Redes de computadoras: El tráfico que se repite
La autosimilitud es muy importante en el diseño de las redes de computadoras. El tráfico de datos en una red (como cuando navegas por internet o descargas un archivo) tiene propiedades autosimilares. Esto significa que los patrones de cómo se mueven los datos se repiten a diferentes escalas de tiempo. Entender esto ayuda a los ingenieros a diseñar redes más eficientes y evitar problemas inesperados.
La Bolsa de Valores: Patrones en los números
Incluso los movimientos de la Bolsa de Valores pueden mostrar un tipo de autosimilitud. Aunque no es una copia exacta, los patrones de subidas y bajadas en los precios pueden parecerse a diferentes escalas de tiempo, si se observan de una manera particular. Esto ayuda a los expertos a estudiar y entender cómo se comportan los mercados financieros.
Galería de imágenes
-
Una curva de Koch presenta una autosimilitud exacta infinitamente repitiente a medida que se aumenta su tamaño.
-
La imagen de un helecho muestra una transformación autosimilar.
Véase también
En inglés: Self-similarity Facts for Kids
- Efecto Droste
- Autorreferencia
- Ley de Zipf
