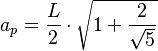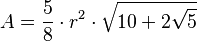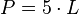Pentágono para niños
Datos para niños Pentágono |
||
|---|---|---|
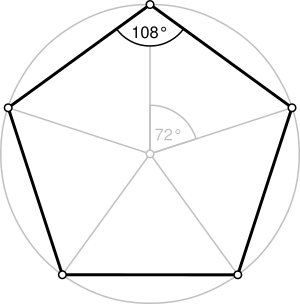
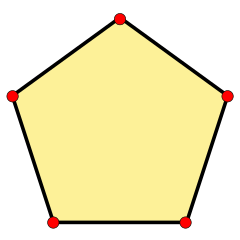 Un pentágono regular
|
||
| Características | ||
| Tipo | Polígono regular | |
| Lados | 5 | |
| Vértices | 5 | |
| Grupo de simetría | 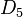 , orden 2x5 , orden 2x5 |
|
| Símbolo de Schläfli | {5} (pentágono regular) | |
| Diagrama de Coxeter-Dynkin | ||
| Polígono dual | Autodual | |
| Área | 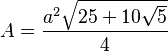 (lado  ) ) |
|
| Ángulo interior | 108° | |
| Propiedades | ||
| Convexo, isogonal, cíclico | ||
Un pentágono es una figura geométrica plana que tiene cinco lados rectos y cinco puntas o esquinas. La palabra "pentágono" viene del griego, donde "pénte" significa "cinco" y "gōnía" significa "ángulo".
La suma de los ángulos internos de cualquier pentágono simple es siempre 540 grados.
Existen diferentes tipos de pentágonos. Algunos son simples, lo que significa que sus lados no se cruzan. Otros pueden ser "auto-intersecantes", como el Estrella pentagonal, que parece una estrella de cinco puntas.
Contenido
¿Qué es un Pentágono Regular?
Un pentágono regular es un tipo especial de pentágono. Se caracteriza por tener:
- Todos sus cinco lados de la misma longitud.
- Todos sus cinco ángulos internos iguales.
Características de un Pentágono Regular
- Cada ángulo interno de un pentágono regular mide 108 grados.
- Es una figura convexa, lo que significa que todas sus puntas "apuntan hacia afuera".
- Cada ángulo externo de un pentágono regular mide 72 grados.
- Un pentágono regular tiene exactamente cinco diagonales. Una diagonal es una línea que conecta dos vértices no consecutivos.
- Se puede dibujar un círculo que pase por todos sus vértices (llamado circunferencia circunscrita). También se puede dibujar un círculo que toque todos sus lados por dentro (llamado circunferencia inscrita).
Propiedades Matemáticas del Pentágono Regular
Apotema
La apotema es la distancia desde el centro de un polígono regular hasta el punto medio de uno de sus lados. Para un pentágono regular con lado L, la apotema (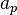 ) se calcula con esta fórmula:
) se calcula con esta fórmula:
Área
El área es la medida de la superficie que cubre el pentágono. Para un pentágono regular de lado L, el área ( ) se puede calcular así:
) se puede calcular así:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = \frac{5L^2}{4}\cot \frac{\pi}{5} \approx 1,72048 L^2
También se puede calcular el área si conoces el radio (r) de la circunferencia que lo rodea:
Perímetro
El perímetro es la suma de las longitudes de todos los lados del pentágono. Para un pentágono regular de lado L, el perímetro (P) es muy sencillo:
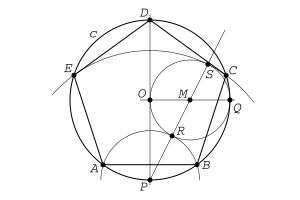
Cómo Construir un Pentágono Regular
Un pentágono regular se puede dibujar usando solo un compás y una regla. Este método fue descrito por el famoso matemático Euclides hace muchísimos años, alrededor del año 300 a.C.
Aquí te explicamos una forma de construirlo dentro de un círculo:
- Dibuja un círculo y marca su centro (llamémoslo O).
- Traza dos líneas que se crucen en el centro O, formando un ángulo de 90 grados (perpendiculares).
- Marca el punto medio de uno de los radios (llamémoslo M).
- Dibuja un pequeño círculo con centro en M que pase por el punto donde la otra línea perpendicular toca el círculo grande.
- Las intersecciones de este pequeño círculo con la línea horizontal te ayudarán a encontrar los puntos para dibujar los lados del pentágono.
- Usando el compás, puedes transferir estas medidas para marcar los cinco vértices del pentágono en el círculo grande.
Al unir los vértices de un pentágono regular, puedes formar un pentagrama (la estrella de cinco puntas) en su interior. Curiosamente, en el centro de ese pentagrama aparecerá otro pentágono regular más pequeño, y así sucesivamente.
Relación con el Número Áureo
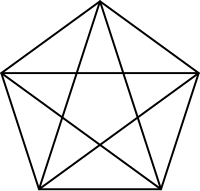
El pentágono regular tiene una conexión especial con un número muy famoso en matemáticas llamado el número áureo (representado con la letra griega φ, "phi"). Este número es aproximadamente 1.618.
Si tomas una diagonal de un pentágono regular y la divides por la longitud de uno de sus lados, ¡el resultado es el número áureo! Esta proporción aparece en muchos lugares de la naturaleza y el arte.
Pentágonos en Mosaicos
¿Sabías que no puedes cubrir una superficie completamente usando solo pentágonos regulares sin dejar huecos o superposiciones? Esto se debe a que el ángulo de 108 grados de un pentágono regular no encaja perfectamente para sumar 360 grados alrededor de un punto.
Sin embargo, existen 15 tipos diferentes de pentágonos que sí pueden cubrir un plano sin dejar huecos. Estos se llaman "teselas pentagonales monoedrales". Son pentágonos que no son regulares, pero que, al repetirse, pueden formar un patrón que cubre toda una superficie.
Otros Tipos de Pentágonos
Pentágonos Equiláteros
Un pentágono equilátero es aquel que tiene todos sus lados de la misma longitud. A diferencia del pentágono regular, sus ángulos internos pueden ser diferentes. Esto significa que hay muchas formas de pentágonos equiláteros, mientras que el pentágono regular es único en su forma.
Pentágonos Cíclicos
Un pentágono cíclico es aquel en el que todos sus vértices (puntas) pueden tocar una misma circunferencia. El pentágono regular es un ejemplo de pentágono cíclico, pero hay muchos otros pentágonos cíclicos que no son regulares.
Véase también
 En inglés: Pentagon Facts for Kids
En inglés: Pentagon Facts for Kids