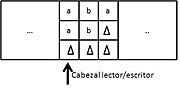
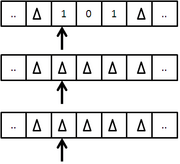
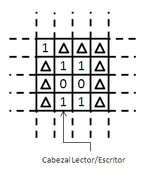
Máquina de Turing para niños
Una máquina de Turing es un modelo teórico de una computadora muy simple. Imagina una máquina que lee y escribe símbolos en una cinta muy larga, siguiendo un conjunto de reglas. Aunque parece sencilla, una máquina de Turing puede simular la lógica de cualquier programa de computadora. Es muy útil para entender cómo funcionan las computadoras y qué problemas pueden resolver.
Fue creada por el matemático inglés Alan Turing en 1936. Él la llamó una "máquina automática". La máquina de Turing no es un aparato real que se construya, sino una idea o un concepto. Ayuda a los científicos a entender los límites de lo que se puede calcular con una máquina.
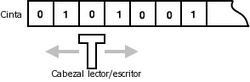
Alan Turing explicó que esta máquina tiene una memoria ilimitada. Esta memoria es como una cinta infinita dividida en cuadrados. En cada cuadrado se puede escribir un símbolo. La máquina solo puede ver un símbolo a la vez. Puede cambiar ese símbolo y su comportamiento depende de lo que ve. La cinta se puede mover hacia adelante y hacia atrás. Así, cualquier símbolo en la cinta puede ser leído o modificado.
Existe una versión especial llamada máquina universal de Turing (MUT). Esta máquina es capaz de simular el comportamiento de cualquier otra máquina de Turing. Esto es como un programa que puede ejecutar cualquier otro programa. El trabajo de Turing se relaciona con el de otro matemático, Alonzo Church. Juntos crearon la tesis de Church-Turing. Esta idea dice que las máquinas de Turing pueden hacer cualquier cálculo que se considere "efectivo" o "algorítmico".
La máquina de Turing es muy importante en la historia de la computación. Fue uno de los primeros modelos teóricos para las computadoras. Además, al estudiar sus propiedades, ha sido la base para muchas ideas en las ciencias de la computación. Esto incluye la teoría de la complejidad computacional, que estudia qué tan difíciles son los problemas para las computadoras. Las máquinas de Turing son simples, lo que facilita su estudio. Sin embargo, no son un modelo práctico para las computadoras modernas, que usan sistemas más rápidos como la memoria RAM.
Contenido
- Historia de la Máquina de Turing
- ¿Cómo funciona una Máquina de Turing?
- Definición y Funcionamiento Formal
- Ejemplos de Funcionamiento de la Máquina de Turing
- Variaciones de la Máquina de Turing
- Máquina de Turing Determinista y No Determinista
- El Problema de la Parada
- Máquina de Turing Universal
- Máquina de Turing Cuántica
- Modelos Similares
- Véase también
Historia de la Máquina de Turing


Alan Turing presentó la idea de la máquina de Turing en un trabajo publicado en 1936. En este estudio, Turing investigaba una pregunta importante: ¿existe un método para saber si cualquier afirmación matemática es verdadera o falsa? Turing diseñó su máquina como un modelo de computadora. Con ella, demostró que hay problemas que ninguna máquina puede resolver.
Con este modelo tan sencillo, se puede realizar cualquier cálculo que una computadora digital moderna pueda hacer.
Gracias a este modelo teórico, fue posible clasificar los problemas que las computadoras pueden resolver. Así surgieron categorías como los problemas "P" y "NP". Estos problemas se refieren a la rapidez con la que una máquina de Turing puede encontrar sus soluciones.
La tesis de Church-Turing, formulada por Alan Turing y Alonzo Church a mediados del siglo XX, explica qué significa que algo sea "computable". La idea principal es que una máquina de Turing es como un autómata que sigue reglas. Tiene una memoria de trabajo ilimitada, pero solo una parte pequeña es accesible en cada momento.
¿Cómo funciona una Máquina de Turing?
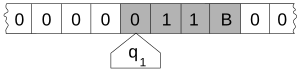
Una máquina de Turing es un modelo matemático de una máquina que trabaja de forma mecánica con una cinta. En esta cinta hay símbolos que la máquina puede leer y escribir. Usa un cabezal que lee o escribe un símbolo a la vez. Su funcionamiento se basa en un conjunto de instrucciones muy simples. Por ejemplo: "si estás en el estado 42 y ves un 0, escribe un 1; si ves un 1, cambia al estado 17".
En su trabajo original, Turing no imaginó un aparato físico. Pensó en una persona que seguía estas reglas de forma mecánica.
Más detalladamente, una máquina de Turing tiene estas partes:
- Una cinta: Es como una tira muy larga dividida en casillas. Cada casilla puede contener un símbolo. La cinta es infinita, es decir, la máquina siempre tiene espacio. Las casillas vacías se llenan con un símbolo especial llamado "blanco".
- Un cabezal: Este cabezal puede leer y escribir símbolos en la cinta. También puede mover la cinta una casilla a la izquierda o a la derecha.
- Un registro de estado: Guarda el "estado" actual de la máquina. Es como el "pensamiento" de la máquina en ese momento. Hay un estado inicial para empezar.
- Una tabla de instrucciones: Es una lista de reglas que le dice a la máquina qué hacer. Cada regla dice: "si estás en este estado y lees este símbolo, entonces haz esto: escribe un nuevo símbolo, mueve el cabezal (izquierda o derecha) y cambia a un nuevo estado".
Cada parte de la máquina (su estado, los símbolos) y sus acciones (escribir, borrar, mover) son finitas y claras. Lo que le da una capacidad ilimitada es la cinta, que puede ser tan larga como se necesite.
Definición y Funcionamiento Formal
Una máquina de Turing es un modelo computacional que lee y escribe automáticamente en una cinta. Esta cinta es la "entrada" y también la "salida".
Este modelo tiene un conjunto de símbolos de entrada y de salida. También tiene un símbolo especial para el "blanco". Además, cuenta con un número limitado de "estados" y reglas para cambiar entre ellos. La máquina empieza en un estado inicial y con una cadena de símbolos en la cinta. En cada paso, lee una casilla, borra el símbolo, escribe uno nuevo y mueve el cabezal. Esto se repite hasta que la máquina llega a un estado final, lo que significa que ha terminado su tarea.
Una máquina de Turing con una sola cinta se puede describir con siete elementos:
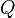 : Un grupo de estados posibles.
: Un grupo de estados posibles. : Los símbolos que la máquina puede leer como entrada (sin incluir el blanco).
: Los símbolos que la máquina puede leer como entrada (sin incluir el blanco).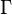 : Todos los símbolos que pueden estar en la cinta (incluyendo los de entrada y el blanco).
: Todos los símbolos que pueden estar en la cinta (incluyendo los de entrada y el blanco).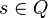 : El estado con el que la máquina empieza.
: El estado con el que la máquina empieza.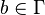 : El símbolo especial para el "blanco".
: El símbolo especial para el "blanco".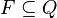 : Los estados donde la máquina se detiene y acepta el resultado.
: Los estados donde la máquina se detiene y acepta el resultado.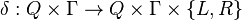 : La función que define las reglas. Dice qué hacer (cambiar de estado, escribir símbolo, mover izquierda 'L' o derecha 'R') según el estado actual y el símbolo leído.
: La función que define las reglas. Dice qué hacer (cambiar de estado, escribir símbolo, mover izquierda 'L' o derecha 'R') según el estado actual y el símbolo leído.
Cómo se mueve la Máquina de Turing
La máquina de Turing tiene un cabezal que lee y escribe en una cinta infinita. Las únicas acciones que puede hacer son:
- Mover el cabezal a la derecha.
- Mover el cabezal a la izquierda.
El cálculo se define por una tabla de estados. Esta tabla indica: (estado actual, símbolo leído) 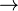 (nuevo estado, nuevo símbolo a escribir, dirección de movimiento).
(nuevo estado, nuevo símbolo a escribir, dirección de movimiento).
La memoria de la máquina es la cinta, dividida en celdas. Al principio, todas las celdas tienen el símbolo "blanco". Las instrucciones de la máquina son como: "si estás en el estado 'x' y lees el símbolo 'z' en la posición 'y', entonces cambia 'z' por otro símbolo y muévete a la izquierda o a la derecha".
Una máquina de Turing puede "reconocer" lenguajes formales. Esto significa que puede procesar y entender ciertos tipos de información. Es más potente que otros modelos más simples, como los autómatas finitos.
Diagramas de Estados
Las máquinas de Turing se pueden representar con dibujos llamados diagramas de estados.
- Los estados son círculos con su nombre dentro.
- Las transiciones (cambios de un estado a otro) son flechas. En la flecha se escribe: "símbolo leído / símbolo escrito, movimiento del cabezal".
- El estado inicial tiene una flecha que llega a él desde ningún sitio.
- Los estados finales se dibujan con un círculo doble.
Ejemplos de Funcionamiento de la Máquina de Turing
Imagina una máquina de Turing que trabaja con los símbolos {0, 1}, donde 0 es el blanco. Esta máquina va a copiar una serie de "1"s. Si la entrada es "11", la máquina la convertirá en "11011". Es decir, duplica la cantidad de "1"s, poniendo un "0" en medio.
Aquí te mostramos cómo se vería el proceso paso a paso para la entrada "11":
| Paso | Estado | Cinta |
|---|---|---|
| 1 | 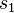 |
11 |
| 2 | 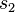 |
01 |
| 3 | 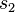 |
010 |
| 4 | 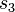 |
0100 |
| 5 | 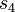 |
0101 |
| 6 | 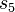 |
0101 |
| 7 | 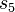 |
0101 |
| 8 | 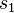 |
1101 |
| 9 | 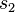 |
1001 |
| 10 | 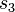 |
1001 |
| 11 | 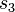 |
10010 |
| 12 | 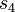 |
10011 |
| 13 | 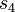 |
10011 |
| 14 | 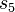 |
10011 |
| 15 | 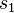 |
11011 |
| Parada | ||
La máquina funciona en un ciclo. Empieza en el estado 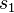 , cambia el primer "1" por un "0" y pasa al estado
, cambia el primer "1" por un "0" y pasa al estado 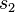 . En
. En 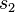 , avanza a la derecha saltando los "1"s hasta encontrar un "0". Cuando lo encuentra, pasa al estado
, avanza a la derecha saltando los "1"s hasta encontrar un "0". Cuando lo encuentra, pasa al estado 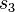 . En
. En 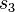 , sigue avanzando a la derecha hasta encontrar otro "0" (la primera vez no habrá "1"s). Una vez al final, añade un "1". Luego, la máquina regresa: en
, sigue avanzando a la derecha hasta encontrar otro "0" (la primera vez no habrá "1"s). Una vez al final, añade un "1". Luego, la máquina regresa: en 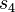 vuelve a la izquierda saltando los "1"s hasta el "0" del medio. Cuando lo encuentra, pasa a
vuelve a la izquierda saltando los "1"s hasta el "0" del medio. Cuando lo encuentra, pasa a 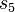 , que sigue a la izquierda hasta el "0" que se escribió al principio. Ese "0" se cambia por un "1". Si el siguiente símbolo es un "1", el ciclo se repite. Si es un "0", significa que la máquina ha terminado y se detiene.
, que sigue a la izquierda hasta el "0" que se escribió al principio. Ese "0" se cambia por un "1". Si el siguiente símbolo es un "1", el ciclo se repite. Si es un "0", significa que la máquina ha terminado y se detiene.
Variaciones de la Máquina de Turing
Existen diferentes versiones de la máquina de Turing, pero todas tienen la misma capacidad para calcular. Esto significa que si un problema puede ser resuelto por una versión, también puede ser resuelto por las otras.
Algunas variaciones incluyen:
- Máquina de Turing con movimiento de espera: Además de moverse a la izquierda o derecha, el cabezal puede quedarse en el mismo lugar.
- Máquina de Turing con cinta infinita a ambos lados: La cinta se extiende infinitamente tanto a la izquierda como a la derecha.
- Máquina de Turing con cinta multipista: Cada casilla de la cinta se divide en varias "subcasillas". Así, una casilla puede guardar varios símbolos a la vez. Solo tiene un cabezal.
- Máquina de Turing multicinta: Tiene más de una cinta y un cabezal para cada una. Cada cinta es infinita.
- Máquina de Turing multidimensional: La cinta se extiende en más de una dirección, como una cuadrícula infinita en 2D.
|
Máquina de Turing Determinista y No Determinista
Una máquina de Turing se llama determinista si para cada combinación de estado y símbolo leído, solo hay una única acción posible. Es como seguir un camino fijo.
Una máquina de Turing es no determinista si para alguna combinación de estado y símbolo, hay varias acciones posibles. Es como si la máquina pudiera "adivinar" el mejor camino o "clonarse" para probar todas las opciones a la vez. Si alguna de esas opciones lleva a una solución, la máquina la acepta.
Aunque su funcionamiento es diferente, ambas tienen la misma capacidad de cálculo. Esto significa que cualquier problema que una máquina no determinista pueda resolver, una determinista también puede, y viceversa. Sin embargo, las máquinas no deterministas pueden resolver algunos problemas mucho más rápido, aunque solo sea en teoría.
El Problema de la Parada
El problema de la parada es una pregunta muy importante en la computación: dada una máquina de Turing y una entrada, ¿podemos saber si la máquina terminará de calcular en un tiempo finito o si seguirá funcionando para siempre?
Alan Turing demostró en su famoso artículo de 1936 que el problema de la parada es indecidible. Esto significa que no existe ninguna máquina de Turing (ni, por lo tanto, ningún programa de computadora) que pueda resolver este problema para todas las posibles máquinas y entradas. Es uno de los límites fundamentales de la computación.
Máquina de Turing Universal
Una máquina de Turing está diseñada para realizar una tarea específica. Es como un programa de computadora o un algoritmo. Pero es posible crear una máquina de Turing que pueda "leer" las instrucciones de cualquier otra máquina de Turing. Esta máquina especial puede simular el comportamiento de cualquier otra.
En 1947, Turing dijo que se podía construir una "máquina especial" que hiciera el trabajo de todas las demás. A esta máquina la llamó "máquina universal".
Gracias a esta idea, una máquina de Turing puede comportarse como cualquier otra. Sin embargo, muchas preguntas sobre el comportamiento de las máquinas de Turing son "indecidibles", como el problema de la parada. Esto significa que no hay un algoritmo que pueda responderlas siempre.
El concepto de Máquina de Turing universal es similar al de un sistema operativo básico. Puede ejecutar cualquier instrucción que sea computable.
Máquina de Turing Cuántica
En 1985, David Deutsch propuso el diseño de la primera Máquina de Turing cuántica. Esta máquina combina las ideas de Turing con los principios de la física cuántica.
Una máquina de Turing cuántica es muy parecida a la clásica, pero con algunas diferencias clave:
- Tiene una cinta de memoria infinita, pero cada elemento es un qubit (la unidad básica de información cuántica).
- Un procesador finito.
- Un cabezal.
El procesador tiene las instrucciones que se aplican al qubit de la cinta. El resultado depende del qubit y del estado del procesador.
Modelos Similares
Existen otros modelos matemáticos que tienen la misma capacidad de cálculo que las máquinas de Turing. Dos de los más conocidos son las máquinas de Post, creadas por Emil Leon Post, y el cálculo lambda, introducido por Alonzo Church y Stephen Kleene en los años 1930. Todos estos modelos son equivalentes en su poder computacional.
|
Véase también
 En inglés: Turing machine Facts for Kids
En inglés: Turing machine Facts for Kids
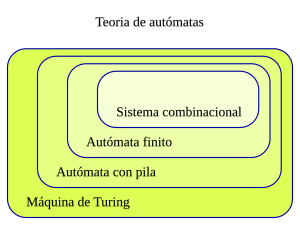
- Teoría de autómatas
- Sistema combinacional
- Autómata finito
- Autómata con pila
- Máquina abstracta
- Máquina de Turing universal
- Máquina de Turing alternante
- Problema de la parada
- Jerarquía de Chomsky
- Juego de la vida
- Cálculo lambda
- Gusanos de Paterson


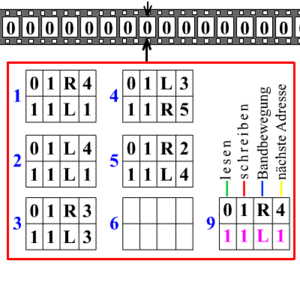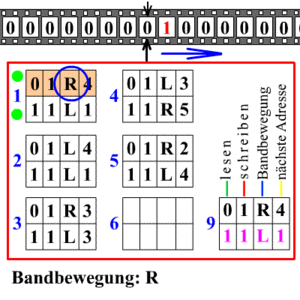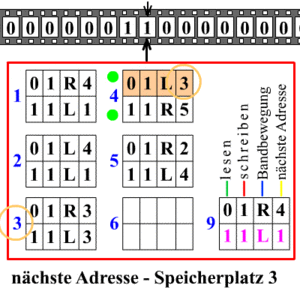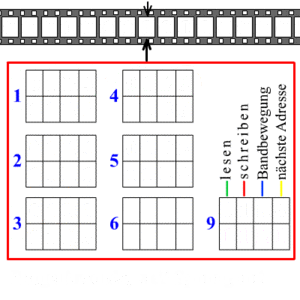
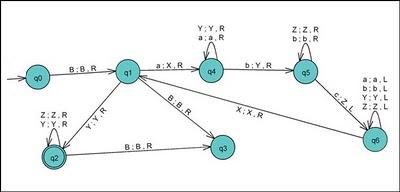
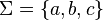 , posee el conjunto de
, posee el conjunto de 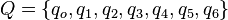 , con las transiciones que se pueden ver. Su estado inicial es
, con las transiciones que se pueden ver. Su estado inicial es 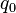 y el estado final es
y el estado final es 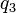 , el lenguaje de salida
, el lenguaje de salida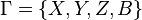 siendo
siendo  el símbolo denominado «blanco». Esta máquina reconoce la expresión regular de la forma
el símbolo denominado «blanco». Esta máquina reconoce la expresión regular de la forma 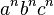 con
con 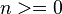 .
.