Lenguaje formal para niños

En matemáticas, lógica y ciencias de la computación, un lenguaje formal es como un idioma muy especial y preciso. A diferencia de los idiomas que hablamos, como el español, los lenguajes formales tienen reglas muy estrictas sobre cómo se forman sus "palabras" y qué símbolos pueden usar.
El conjunto de símbolos básicos que se pueden usar se llama el alfabeto (o vocabulario) del lenguaje. Las reglas para combinar esos símbolos se llaman la gramática formal (o sintaxis). Una secuencia de símbolos que sigue estas reglas se conoce como una fórmula bien formada (o palabra) del lenguaje. En resumen, un lenguaje formal es el conjunto de todas sus fórmulas bien formadas.
Por ejemplo, un alfabeto podría ser solo dos símbolos: a y b. Una regla de la gramática podría decir que las fórmulas bien formadas son aquellas que tienen la misma cantidad de símbolos a que de símbolos b. Así, algunas fórmulas válidas serían: ab, ba, abab, ababba, etc. El lenguaje formal sería el conjunto de todas estas combinaciones válidas.
Algunos lenguajes formales tienen una semántica formal, que les da un significado a sus fórmulas. Sin embargo, no todos los lenguajes formales necesitan tener un significado para existir, lo cual es una gran diferencia con los lenguajes naturales (como el español).
En algunos lenguajes formales, se permite la "palabra vacía", que es una secuencia de símbolos de longitud cero. Se suele representar con símbolos como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \varepsilon \, ,  o
o 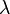 .
.
Contenido
¿Qué son los lenguajes formales?
Los lenguajes formales son herramientas muy útiles en diferentes campos.
Ejemplos de lenguajes formales
Aquí tienes algunos ejemplos de dónde se usan los lenguajes formales:
- El conjunto de todos los programas que están bien escritos en un lenguaje de programación específico.
- El conjunto de todas las fórmulas válidas en la lógica de primer orden, que es un sistema para razonar.
¿Cómo se definen los lenguajes formales?
Los lenguajes formales se pueden definir de varias maneras, por ejemplo:
- Mediante gramáticas formales: Son reglas que explican cómo se pueden construir las palabras del lenguaje. Esto se estudia en la jerarquía de Chomsky.
- Mediante expresiones regulares: Son patrones que describen las cadenas de símbolos que pertenecen al lenguaje.
- Mediante autómatas: Son modelos matemáticos que pueden "aceptar" o "reconocer" las cadenas de símbolos que forman parte del lenguaje, como una máquina de Turing o un autómata finito.
Las cadenas de símbolos se forman siguiendo dos aspectos principales:
- Sintaxis: Se refiere a las reglas de cómo se combinan los símbolos para formar estructuras válidas.
- Semántica: Se refiere al significado de esas estructuras válidas.
Operaciones con lenguajes formales
Podemos combinar lenguajes formales para crear nuevos lenguajes. Imagina que L1 y L2 son dos lenguajes que usan el mismo alfabeto.
- La concatenación L1L2: Consiste en unir una palabra de L1 con una palabra de L2. Por ejemplo, si L1 tiene "hola" y L2 tiene "mundo", la concatenación podría ser "holamundo".
- La unión L1|L2: Incluye todas las palabras que están en L1 o en L2 (o en ambos).
- La intersección L1&L2: Incluye solo las palabras que están tanto en L1 como en L2.
- La estrella L1* (también llamada clausura de Kleene): Consiste en todas las palabras que se pueden formar repitiendo cero o más veces las palabras de L1. Esto incluye la palabra vacía.
- La clausura positiva L1+: Es similar a la estrella, pero las palabras de L1 deben repetirse al menos una vez. No incluye la palabra vacía a menos que L1 ya la contenga.
Lenguajes libres de contexto
Los lenguajes libres de contexto son un tipo importante de lenguajes formales. Sus reglas de gramática son muy útiles para definir la estructura de muchos lenguajes de programación.
Las gramáticas libres de contexto funcionan como una lógica para definir la sintaxis de los lenguajes. Las definiciones son inductivas, lo que significa que las propiedades de una cadena de símbolos se determinan por las propiedades de sus partes más pequeñas. Por ejemplo, una regla podría decir que si una cadena "aSb" es válida, entonces "aaSbb" también lo es.
En 1956, Noam Chomsky creó la jerarquía de Chomsky para clasificar los diferentes tipos de lenguajes formales según la complejidad de sus gramáticas.
Véase también
 En inglés: Formal language Facts for Kids
En inglés: Formal language Facts for Kids
- Teoría de la computación
- Ciencias de la computación
- Lenguaje de especificación
- Lenguaje formalizado
- Notación matemática
- Gramática libre de contexto

