Intersección de conjuntos para niños
La intersección de dos o más conjuntos es una operación que nos ayuda a encontrar los elementos que tienen en común. Imagina que tienes dos grupos de cosas; la intersección sería como una lista de las cosas que están en ambos grupos al mismo tiempo.
Por ejemplo, si tenemos un conjunto de números pares (P) y un conjunto de números cuadrados (C), su intersección sería el conjunto de los números que son pares y cuadrados a la vez.
- P = {2, 4, 6, 8, 10, 12, 14, 16, ...} (todos los números pares)
- C = {1, 4, 9, 16, 25, ...} (todos los números que resultan de multiplicar un número por sí mismo, como 1x1=1, 2x2=4, 3x3=9)
La intersección de P y C sería D = {4, 16, 36, 64, ...} porque estos números son pares y también son cuadrados.
Otro ejemplo: Si el conjunto A = {a, b, c, d, e, f} y el conjunto B = {a, e, i, o, u}, entonces la intersección de A y B es {a, e}. Esto es porque 'a' y 'e' son los únicos elementos que se encuentran en ambos conjuntos.
El símbolo que usamos para la intersección es ∩. Así, podemos escribir D = P ∩ C.
Contenido
¿Qué es la Intersección?
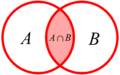
La intersección de dos conjuntos, digamos A y B, es un nuevo conjunto que solo contiene los elementos que pertenecen tanto a A como a B. Es como encontrar el "terreno común" entre ellos.
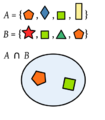
Por ejemplo, si A = { π, c, 8, γ, 5, P } y B = { ω, c, 0, Δ, 5, R }. La intersección de A y B es A ∩ B = { 5, c }. Los elementos '5' y 'c' son los únicos que están en ambos conjuntos.
Ejemplos de Intersección
- Imagina el conjunto C de números que son potencias de 2 (como 2, 4, 8, 16, 32, 64...) y el conjunto D de números que son cubos (como 1, 8, 27, 64, 125...).
La intersección de C y D sería C ∩ D = {8, 64, 512, ...}. Estos números son potencias de 2 y también son cubos.
- Si tenemos el conjunto de números pares y el conjunto de números impares, ¿cuál sería su intersección? Sería el conjunto vacío (∅). Esto significa que no hay ningún número que sea par e impar al mismo tiempo.
Conjuntos Disjuntos: Cuando no hay Elementos Comunes
Cuando la intersección de dos conjuntos es el conjunto vacío (∅), decimos que esos conjuntos son disjuntos. Esto significa que no tienen ningún elemento en común.
Por ejemplo, el conjunto de los números pares y el conjunto de los números impares son disjuntos.
Propiedades de la Intersección
La intersección de conjuntos tiene algunas propiedades interesantes, parecidas a las operaciones que hacemos con números:
Propiedades Básicas
- Idempotencia: Si intersectas un conjunto consigo mismo, el resultado es el mismo conjunto.
* A ∩ A = A
- La intersección de A y B siempre será un subconjunto de A y también un subconjunto de B. Esto significa que todos los elementos de la intersección están contenidos en A y en B.
* A ∩ B ⊆ A * A ∩ B ⊆ B
- Si un conjunto B está completamente dentro de un conjunto A (B ⊆ A), entonces la intersección de A y B es simplemente B.
* Si B ⊆ A, entonces A ∩ B = B
Propiedades con la Unión
La intersección también se relaciona con la unión (que es cuando juntamos todos los elementos de dos conjuntos).
- Propiedad asociativa: No importa cómo agrupes los conjuntos al intersectarlos, el resultado será el mismo.
* (A ∩ B) ∩ C = A ∩ (B ∩ C)
- Propiedad conmutativa: El orden en que intersectas los conjuntos no cambia el resultado.
* A ∩ B = B ∩ A
- Elemento absorbente: La intersección de cualquier conjunto A con el conjunto vacío (∅) siempre es el conjunto vacío. Es como si el conjunto vacío "absorbiera" todo.
* A ∩ ∅ = ∅
- Propiedad distributiva: La intersección se puede "distribuir" sobre la unión, y viceversa.
* A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) * A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
Galería de imágenes
-
La intersección de A y B es otro conjunto A ∩ B que contiene solo los elementos que pertenecen tanto a A como a B.
-
Intersección de dos conjuntos A y B.
-
La intersección de dos superficies oblicuas.
-
Intersección de 3 conjuntos (diagrama de Venn).
Véase también
- Álgebra de conjuntos
- Conjunto
- Teoría de conjuntos
- Unión de conjuntos
Literatura del tema
- Dorronsoro, José y Hernández, Eugenio. Números, grupos y anillos. Addison-Wesley/Universidad Autónoma de Madrid, 1996.
- Lipschutz, Seymour. Teoría de conjuntos y temas afines. McGraw-Hill, 1991.
