Estructura algebraica para niños
Una estructura algebraica es como un conjunto de reglas especiales que nos dicen cómo podemos combinar elementos de un grupo de cosas. Imagina que tienes un grupo de números y una forma de combinarlos, como la suma o la multiplicación. Una estructura algebraica nos dice qué propiedades tiene esa combinación.
En el álgebra abstracta, que es una rama de las matemáticas, estudiamos estas estructuras. Es como si tuviéramos un "kit de construcción" matemático. El kit incluye:
- Un conjunto de elementos (por ejemplo, números, letras o formas).
- Una o más operaciones (como sumar, restar, multiplicar o dividir) que podemos usar con esos elementos.
Lo interesante es que estas operaciones deben seguir ciertas reglas o propiedades para que el conjunto y las operaciones formen una estructura algebraica específica.
Contenido
¿Qué son las estructuras algebraicas?
Las estructuras algebraicas nos ayudan a entender cómo funcionan diferentes sistemas matemáticos. Al estudiar sus propiedades, los matemáticos pueden descubrir cosas nuevas sobre los números, las formas y otros conceptos. Es como clasificar diferentes tipos de juegos de mesa según sus reglas.
Propiedades importantes en las estructuras
Para que un conjunto y una operación formen una estructura algebraica, deben cumplir ciertas propiedades. Algunas de las más comunes son:
¿Qué es la asociatividad?
La propiedad asociativa significa que el orden en que agrupas los elementos no cambia el resultado. Por ejemplo, en la suma: (2 + 3) + 4 es lo mismo que 2 + (3 + 4). Ambos dan 9.
¿Qué es el elemento neutro?
El elemento neutro es un elemento especial que, al combinarlo con cualquier otro, no lo cambia.
- Para la suma, el elemento neutro es el 0 (cero), porque 5 + 0 = 5.
- Para la multiplicación, el elemento neutro es el 1 (uno), porque 5 × 1 = 5.
¿Qué es el elemento simétrico?
El elemento simétrico (o inverso) es aquel que, al combinarlo con otro elemento, da como resultado el elemento neutro.
- Para la suma, el simétrico de 5 es -5, porque 5 + (-5) = 0 (el neutro de la suma).
- Para la multiplicación, el simétrico de 5 es 1/5, porque 5 × (1/5) = 1 (el neutro de la multiplicación).
¿Qué es la conmutatividad?
La propiedad conmutativa significa que el orden de los elementos no cambia el resultado. Por ejemplo, en la suma: 2 + 3 es lo mismo que 3 + 2. Ambos dan 5.
¿Qué es la distributividad?
La propiedad distributiva relaciona dos operaciones. Por ejemplo, la multiplicación es distributiva sobre la suma: 2 × (3 + 4) es lo mismo que (2 × 3) + (2 × 4). Ambos dan 14.
Ejemplos de estructuras algebraicas
Existen muchas estructuras algebraicas, cada una con sus propias reglas. Aquí te presentamos algunas de las más conocidas:
¿Qué es un grupo?
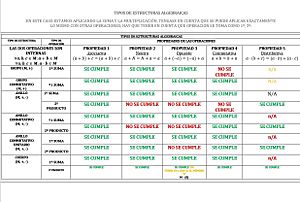
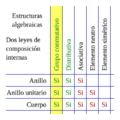
Un grupo es un conjunto con una sola operación que cumple estas cuatro propiedades:
- Es asociativa.
- Tiene un elemento neutro.
- Cada elemento tiene un elemento simétrico.
- El resultado de la operación siempre está dentro del conjunto (se llama "cerrada").
Un ejemplo de grupo son los números enteros (..., -2, -1, 0, 1, 2, ...) con la operación de la suma.
¿Qué es un anillo?
Un anillo es un conjunto con dos operaciones, generalmente llamadas "suma" y "multiplicación". Estas operaciones deben cumplir varias propiedades:
- Con la suma, el conjunto forma un grupo conmutativo (también llamado "grupo abeliano").
- La multiplicación es asociativa.
- La multiplicación es distributiva sobre la suma.
Los números enteros con la suma y la multiplicación son un ejemplo de anillo.
¿Qué es un cuerpo?
Un cuerpo es un tipo especial de anillo. Además de todas las propiedades de un anillo, un cuerpo tiene una propiedad extra muy importante:
- Todos los elementos del conjunto (excepto el elemento neutro de la suma) tienen un elemento simétrico para la multiplicación.
Los números racionales (fracciones), los números reales y los números complejos son ejemplos de cuerpos.
Galería de imágenes
-
Diagrama de estructuras con una ley de composición interna.
-
Diagrama de estructuras con dos leyes de composición interna.
Véase también
En inglés: Algebraic structure Facts for Kids
