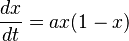Sistema dinámico para niños
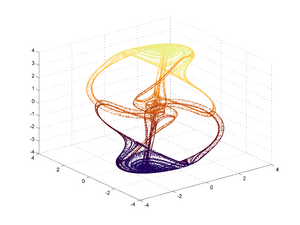
Un sistema dinámico es como un conjunto de cosas que cambian con el tiempo. Imagina el clima, la población de animales o incluso cómo se mueve un péndulo; todos son ejemplos de sistemas dinámicos. Su estado, es decir, cómo se ven en un momento dado, evoluciona y se transforma.
Podemos encontrar sistemas dinámicos en la naturaleza, como el movimiento de los planetas, pero también en modelos que creamos para entender el mundo, como los que usan los economistas o los matemáticos. Para estudiar estos sistemas, primero definimos sus límites: qué elementos forman parte de él y cómo se relacionan entre sí. Así, podemos crear modelos que nos ayuden a entender su estructura y cómo se comportan.
El tiempo en estos sistemas puede medirse de diferentes maneras: en pasos discretos (como los años en un calendario) o de forma continua (como el tiempo que pasa sin interrupciones). En cualquier momento, un sistema dinámico tiene un "estado", que es como una foto de cómo está en ese instante. La "regla de evolución" es la que nos dice cómo ese estado cambiará en el futuro. A veces, el cambio es predecible (determinista), y otras veces, los eventos aleatorios también influyen (estocástico).
En la física, un sistema dinámico se describe como partículas o grupos de partículas que cambian con el tiempo. Para predecir su futuro, los científicos usan ecuaciones especiales o simulaciones por computadora. El estudio de los sistemas dinámicos es muy importante y se aplica en muchos campos, como las matemáticas, la física, la biología, la química, la ingeniería y la medicina. También son clave para entender conceptos como la teoría del caos, que estudia comportamientos que parecen aleatorios.
Contenido
¿Cómo se estudian los sistemas dinámicos?
El estudio de los sistemas dinámicos comenzó con la mecánica newtoniana, que describe el movimiento. Al principio, para saber cómo evolucionaría un sistema, se usaban ecuaciones que solo mostraban el cambio en un corto periodo. Para ver el futuro a largo plazo, había que repetir el cálculo muchas veces, paso a paso. Este proceso se llama "resolver el sistema". Si se puede resolver, podemos conocer todas las posiciones futuras de un sistema a partir de un punto inicial, lo que se conoce como su "trayectoria" u "órbita".
Antes de que existieran los ordenadores, era muy difícil calcular estas trayectorias. Solo se podía hacer para sistemas muy sencillos. Pero con la llegada de las computadoras, se hizo mucho más fácil.
Para sistemas sencillos, conocer la trayectoria es suficiente. Sin embargo, la mayoría de los sistemas dinámicos son muy complejos. Esto se debe a varias razones:
- Conocimiento aproximado: A veces no conocemos los sistemas con total precisión. Para manejar esto, se estudian conceptos como la "estabilidad", que significa que el sistema se comporta de manera similar incluso con pequeños cambios.
- Tipos de trayectoria: No siempre importa la trayectoria exacta, sino el tipo de comportamiento. Algunas trayectorias pueden ser repetitivas (periódicas), mientras que otras pueden explorar muchos estados diferentes.
- Cambios por parámetros: El comportamiento de un sistema puede cambiar drásticamente si se modifica un valor específico, lo que se conoce como "puntos de bifurcación". Por ejemplo, un fluido puede pasar de un movimiento suave a uno caótico (turbulencia).
- Comportamiento errático: Algunas trayectorias pueden parecer aleatorias. En estos casos, se calculan promedios a lo largo de mucho tiempo o con muchas trayectorias diferentes para entender el comportamiento general.
Historia de los sistemas dinámicos
Muchos consideran al matemático francés Henri Poincaré como el fundador de los sistemas dinámicos. A finales del siglo XIX, Poincaré publicó trabajos importantes donde aplicó sus ideas al problema del movimiento de tres cuerpos celestes, estudiando cómo se comportaban sus soluciones. Él demostró que algunos sistemas, después de un tiempo, volverán a un estado muy parecido al inicial.
Aleksandr Lyapunov desarrolló métodos para entender la estabilidad de los sistemas dinámicos a finales del siglo XIX. Su trabajo es la base de la teoría moderna de la estabilidad.
En 1913, George David Birkhoff demostró un teorema importante de Poincaré, lo que le dio fama mundial. Más tarde, en 1931, descubrió el "teorema ergódico", que es fundamental para entender cómo se comportan los sistemas a largo plazo.
Stephen Smale también hizo grandes avances, como el "Herradura de Smale", que impulsó mucha investigación en este campo.
En 1964, Oleksandr Mykolaiovych Sharkovsky desarrolló un teorema sobre los periodos de los sistemas dinámicos discretos. Una de sus ideas es que si un sistema tiene un comportamiento que se repite cada 3 pasos, entonces también tendrá comportamientos que se repiten en cualquier otro número de pasos.
A finales del siglo XX, el ingeniero Ali H. Nayfeh aplicó la dinámica no lineal en la ingeniería. Su trabajo fue muy importante para el diseño y mantenimiento de máquinas y estructuras que usamos a diario, como barcos, grúas, puentes, edificios, aviones y naves espaciales.
Elementos clave para entender un sistema dinámico
Cuando creamos modelos para estudiar un sistema dinámico, es importante considerar:
- Un sistema está formado por varias partes que interactúan entre sí.
- Podemos mostrar cómo se comporta el sistema usando diagramas que explican las relaciones de causa y efecto.
- Hay dos tipos de variables: las "exógenas", que afectan al sistema desde fuera (como un cambio en el clima que afecta una población), y las "endógenas", que son causadas por el propio sistema (como el número de nacimientos en una población).
Ejemplo sencillo de un sistema dinámico
Imagina una especie de peces en un lago. Si este año la cantidad de peces es `Xk`, el próximo año será `Xk+1`. Podemos darle nombres a la cantidad de peces cada año: `X0` para el año inicial, `X1` para el primer año, y así sucesivamente hasta `Xk`.
La cantidad de peces del próximo año (`Xk+1`) depende de la cantidad de peces de este año (`Xk`). Esto se puede escribir como una fórmula: `Xk+1 = f(Xk)`. Esta ecuación representa un sistema dinámico, porque nos muestra cómo la cantidad de peces cambia con el tiempo.
Tipos de sistemas dinámicos
Los sistemas dinámicos se clasifican en dos tipos principales según cómo se mide el tiempo:
- Sistemas discretos: El tiempo se mide en pasos o lapsos pequeños. Se modelan con relaciones que se repiten, como la ecuación logística:
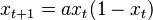
Aquí, `t` representa los pasos de tiempo (por ejemplo, años) y `x` es la variable que cambia.
- Sistemas continuos: El tiempo se mide de forma continua, sin interrupciones. Se expresan con ecuaciones diferenciales, por ejemplo:
En este caso, `x` es la variable que cambia continuamente con el tiempo `t`.
Sistemas lineales y no lineales
También distinguimos entre sistemas dinámicos "lineales" y "no lineales":
- Sistemas lineales: Son más sencillos de analizar. En sus ecuaciones, las variables se relacionan de forma directa y proporcional. Por ejemplo:
Si conoces dos soluciones para un sistema lineal, puedes sumarlas y el resultado también será una solución. Esto simplifica mucho su estudio.
- Sistemas no lineales: Son mucho más complejos de analizar. A menudo, pueden mostrar un comportamiento que parece totalmente impredecible, conocido como caos. Esto significa que un cambio muy pequeño al principio puede llevar a resultados muy diferentes a largo plazo.
Véase también
 En inglés: Dynamical system Facts for Kids
En inglés: Dynamical system Facts for Kids
- No linealidad
- Dinámica de sistemas
- Cibernética
- Teoría de sistemas
- Realimentación
- Sistema de control